线性扫描和二分查找哪个快

Posted 2021-04-10 数据极客

在一个有序向量中查找元素，线性扫描和二分查找哪个快？这似乎是个很显然的问题。据说有90%的人在面试时无法写出没有bug的二分查找，而实际上根据笔者的经验来看，这个比例还要高，因此所有拿着高薪的程序员都该感谢这个时代给予的机会。

扯远了，回到这个问题本身。先看看最简单的线性扫描：

每个循环有2个条件分支，一个用于检查当前游标是否越界，另一个用于检查是否找到了需要查找的元素。众所周知，程序执行的分支语句越多，就越不利于性能优化。为了加速程序的执行，我们需要指令预测以减少分支的数量，比如下面这种改进：

这段代码可以平均把每次循环的分支从2减少到1.25，当然如果向量长度n小于4，那就没有任何优化了。

还有一种优化技巧是彻底拿掉一个分支，把边界检查移走：

这样，每次循环就只有一次分支预测指令了。

我们还可以用SIMD指令来加速上面的程序，比如我们可以一次把4个整数加载到一个128位的寄存器中，然后用PCMPGTD指令同时进行4次比较，比较的结果用PMOVMSKB存放在另一个寄存器中，如果结果显示有一次比较命中，可以利用BSF指令获得究竟是这4个整数的哪一个：BSF指令返回寄存器中低位比特0的数目，因此对应寄存器中整数索引，代码如下：

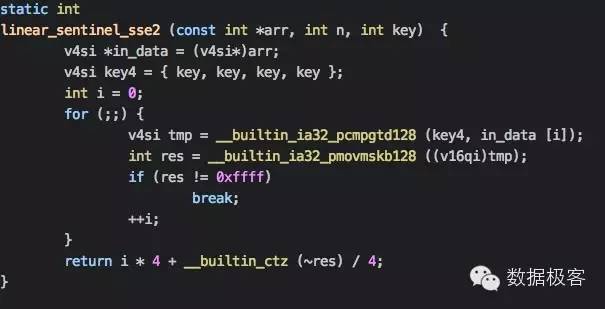
请注意这段代码要求我们在数组向量的最后要做好128位对齐操作，否则会因为指针越界引发段错误。这段程序可以让我们每4个元素才有一次分支预测，然而，我们可以继续利用PACKSSDW和PACKSSWB进一步改进到每16个元素才有一次分支预测，当然这需要在数组后边补充更多的dummy元素：

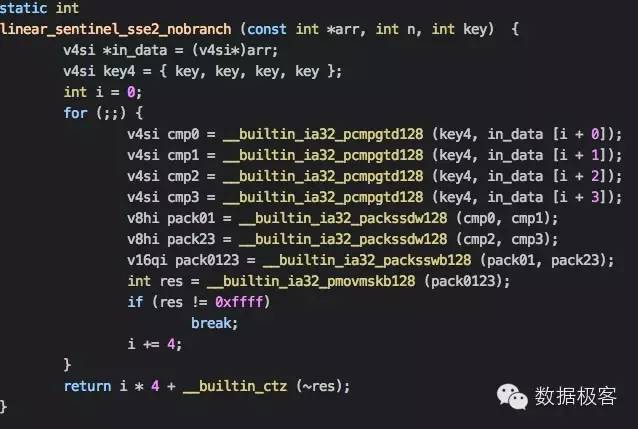
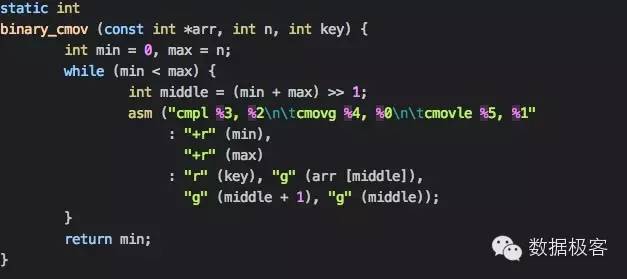
下边来看二分查找，这是一段基本的二分查找代码：

每次迭代有2次分支预测，但它们并不像线性扫描那样可预测，因此对于CPU来说这可能会发生预测错误，这对性能的影响比可预测的分支要更大。下边这段代码通过汇编转化成为可预测的分支，因此执行速度快于普通的二分查找。

那么线性扫描和二分查找哪个快呢？这不是一个单纯比较算法复杂度的问题，真实结果取决于向量数组的长度，在小长度的向量查找时，线性扫描会更快速，而较大的数组则采用二分查找更适合。根据实验结果[1]，这个分界的阀值在64到128，究竟什么是更适合的阀值，这取决于硬件特性，最好还是亲自测试才能得出结论。而采用SIMD加速的线性扫描，则比普通的线性扫描快1到5倍，具体也取决于硬件和数组长度：

上面的代码里，我们利用SIMD指令对线性扫描进行了加速，那么能否也利用SIMD对二分查找进行加速呢？答案也是可以的[2]：基本思想是，把向量划分成为5个子空间，这样需要4个边界值，利用SIMD指令和边界值进行子空间的选区，然后只在某个子空间内进行二分查找检索，这样就减少了指令执行的次数，伪代码如下：

完整的性能测试代码在[2]，请大家在自己的电脑上自行验证。有朋友会问，这种性能优化有多少实际价值？举个典型场景，倒排索引为了追求极致性能，会涉及到大批量整数的压缩和处理，而优秀的压缩算法无一例外地涉及到分块压缩，因此最终的倒排链求交或者求并等运算，都涉及到对解压后某区块内的检索和比较，这时就涉及到在线性扫描和二分查找之间做对比了，一个良好的设计应当根据阀值来动态做出选择并进行SIMD加速处理，笔者之前团队的工作就是这样来处理，取得了压缩之外显著的细节提升。凡是涉及到频繁读取数组的场景，这种小处着眼点的优化都会带来显著收益。

祝玩得开心。

[1] https://github.com/schani/linbin

[2] https://github.com/WojciechMula/simd-search