带你快速记住二分查找算法

Posted 2021-04-10 搜狗测试

小编所在的项目近期对一些年代久远的函数进行了算法上的升级和优化，其中有笔提交，改动很小，但是优化算法效率高达十几倍，给小编留下了深刻的印象。这笔提交就是利用了二分查找算法，呐这篇文章就是带你了解什么是二分查找算法，以及如何快速记住二分查找算法。

有的人也许说二分查找很简单，让我们看看大佬Knuth是怎么形容的：

Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky…

思路很简单，细节是魔鬼。

二分查找算法 ※ 简介

二分查找就是将查找的键和子数组的中间键作比较，如果被查找的键小于中间键，就在左子数组继续查找；如果大于中间键，就在右子数组中查找，否则中间键就是要找的元素。

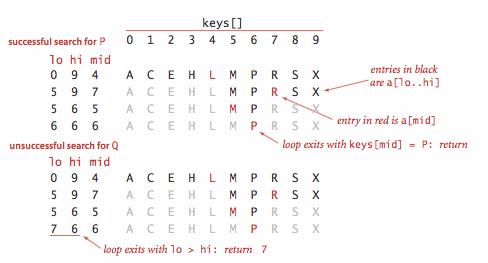
基本实现：

public int binarySearch(int[] A, int target, int n){
    int low = 0, high = n - 1, mid;
    while(low <= high){
        mid = low + (high - low) / 2;
        if(A[mid] == target){
            return mid;
        }else if(A[mid] > target){
            high = mid - 1;
        }else{
            low = mid + 1;
        }
    }
    return -1;
}

注意事项：

1. 循环的判定条件是：

    low <= high
2. 为了防止数值溢出：

    mid = low + (high - low)/2
3. 当 A[mid]不等于target时，

    high = mid - 1或low = mid + 1

二分查找算法 ※ 应用

以上介绍的算法是最简单的二分查找算法，但是在实际应用中二分查找算法更加复杂，比如：数组之中的数据可能可以重复，要求返回匹配的数据的最小（或最大）的下标；更近一步， 需要找出数组中第一个大于key的元素（也就是最小的大于key的元素的）下标，等等。

这些虽然只有一点点的变化，实现的时候让人非常头疼。用一个办法可以快速的写出符合需求的二分查找算法，即边界查找法。

例如在一群有序数组里面查找（允许重复）查找第一个相等于key的元素，也就是说等于查找key值的元素有好多个，返回这些元素最左边的元素下标。『....5, 6, 6, 7, 8....』

那么我们寻找的边界就是5，6，我们终止的判断条件是low <= high，且间隔为1，所以这个时候返回也就是当high = 5，low = 6的时候，这个时候return的值为low。另外就是要判断A[mid] ? key中的表达式，如果我第一次找到了3，那么low值就应对着增加所以是判断符号为<=，这种问题都带入以下的框架解决，只要找到边界值，再根据题目确认下判断符号即可。

while (low <= high) {
    int mid = low + (high - low)/2;
    if (A[mid] ? key) {
        //... low = mid + 1;
    }
    else {
        // ...high = mid - 1;
    }
}
return ？;

如果在项目中实际应用的话，std也对二分查找算法进行了封装，lower_bound( first, last,val)返回值是一个迭代器,返回指向大于等于val的第一个值的位置, upper_bound(first, last, val)算法返回大于等于key的最后一个元素位置，如果没有重复的值，两者的返回位置相同。

二分查找算法 ※ 记忆

总结下二分查找的特点，有一个快速记住二分查找算法的秘诀。

22233，该算法有两个名字（二分查找、折半查找）;  两个缺点（待查找表为有序表、插入删除困难) ; 两种实现方式（递归、非递归）; 三个优点（比较次数少、查找速度快、平均性能好）; 三个实现的注意事项（low<=high, mid = low + (high - low)/2, high = mid - 1或low = mid + 1）。

愿平安遂意