13.从13亿次到31次，神奇的“二分查找”

Posted 2021-04-10 和孩子一起学Python

、、

二分查找

   

    在列表中查找符合条件的元素，需要遍历整个列表，逐个元素检查。

    上一篇介绍过，遍历列表有2种方式。

import randoma = random.sample(range(1,100),80)
for x in a: if 88 == x: print("列表里有88") breakelse: print("列表里没有88")

    

import randoma = random.sample(range(1,100),80)
for i in range(0,len(a)): if 88 == a[i]: print("第%d个元素是88"%(i+1)) breakelse:    print("列表里没有88")

    第一种方式看上去更简单，但一般情况下，我们不仅需要找到这个元素，还需要知道元素在列表中的位置，所以，反而第二种方式用得更多。

   

    

无处不在的查找

    查找恐怕是这个世界上每天发生得最多的事情了。尤其是在互联网上。  

    我们每天

    在百度上查找资料

    在淘宝、京东上查找商品

    在QQ音乐、网易音乐上查找歌曲

    在晋江查找小说

    ……

    但可能我们都没有思考过一个问题，电脑是如何从数以亿计的海量数据里找到我们想要？我们试着用一个简单的例子来说明海量数据的查找其实是一件很有技术含量的事情。

    比如说办理护照，窗口的工作人员要你提供身份证号码，然后在电脑上输入你的身份证号码，查找核实你的资料。

    我们假设，全国所有人的身份证号码都保存在一个列表里。那么这个列表就有13亿多个元素。按照我们文章开头介绍的方法，每次查找都需要遍历整个列表，最差的情况就需要找13亿次。

    我们知道电脑的速度很快，1秒钟甚至可以找1000万次。

    可是 13亿/1000万 = 130秒 ，需要 2 分多钟。

    真的需要这么长时间吗？有没有更快的办法？

    

神奇的“二分查找”

    假设下面的列表，一共有13亿个数字

    最小是3，最大是100亿。

    数字从小到大排列，但没有规律。

    需要在里面查找数字 x = 314159260

    需要从第一个元素依次往后查找吗？

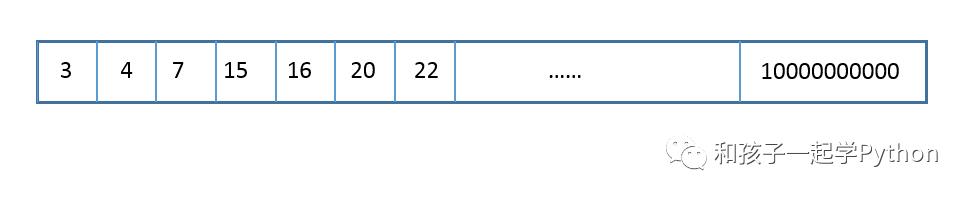
    显然不需要。因为数字有序！

    拿x和列表中间的元素比较，如果相等，就找到了。

    如果 x 比中间元素大，显然，我们只需要在中间元素右边里继续查找。

    反之亦然。

    这样，每次都可以把查找的范围缩小一半。

    这就是“二分查找”

    

    最多需要查找多少次呢？

    其实就是求 n 除以多少次2之后等于1。

    也就是数学上以2为底的对数函数：log2(n)

 

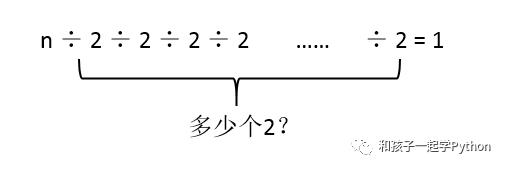
    math模块提供了以2为底的对数函数 log2()。

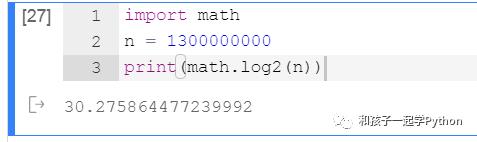
    也就是说最坏的情况，也只需要31次，就能完成！

    和13亿次相比，简直是天壤之别。

    这就是“二分查找”的神奇之处。

Python实现“二分查找”

    我们先生成一个从0到1亿的数列。

    注意：range()函数返回的并不是列表类的实例，但是是可以被循环的数列，所以满足我们的需求。

l1 = range(0,100000000)

    然后我们去查找一个不可能存在的数字， x = 100000001。

    当然，你没有上帝视角，并不知道这个数字不存在。

    所以在学会“二分查找”之前，只能逐一查找。

    我们再介绍一个新的模块 datetime. 它有函数可以返回程序执行时的时间。

    

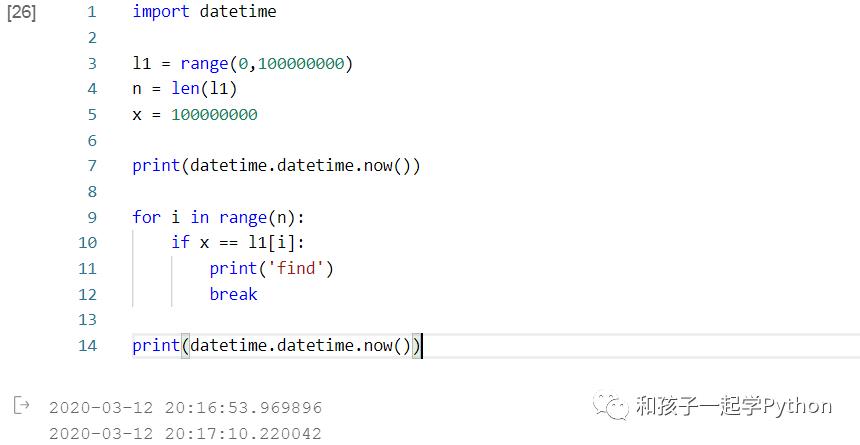
    在for循环查找之前，和查找结束后。

    我们分别用 print(datetime.datetime.now())打印出当时的时间。

    然后2个时间相减就是查找用的时间。

    我们发现，要完成1亿次查找，电脑用了将近 16 秒钟！

    和人相比，已经非常非常快了。

    但如果是十亿，甚至百亿、千亿的数据，这个速度就太慢，太慢了！

    如果用“二分查找”呢？

    准备查找

    列表的最左边位置   left = 0 

    最右边位置  right = len(l1) - 1

    中间位置  mid = (left+right) // 2

    

    开始查找

    x 和 中间位置的元素做比较， if x == l1[mid]

    如果相等，break 结束。

    如果 x 更大，下次只需要查找 mid 右边的元素，也就是   left = mid +1

    反之 right = mid - 1

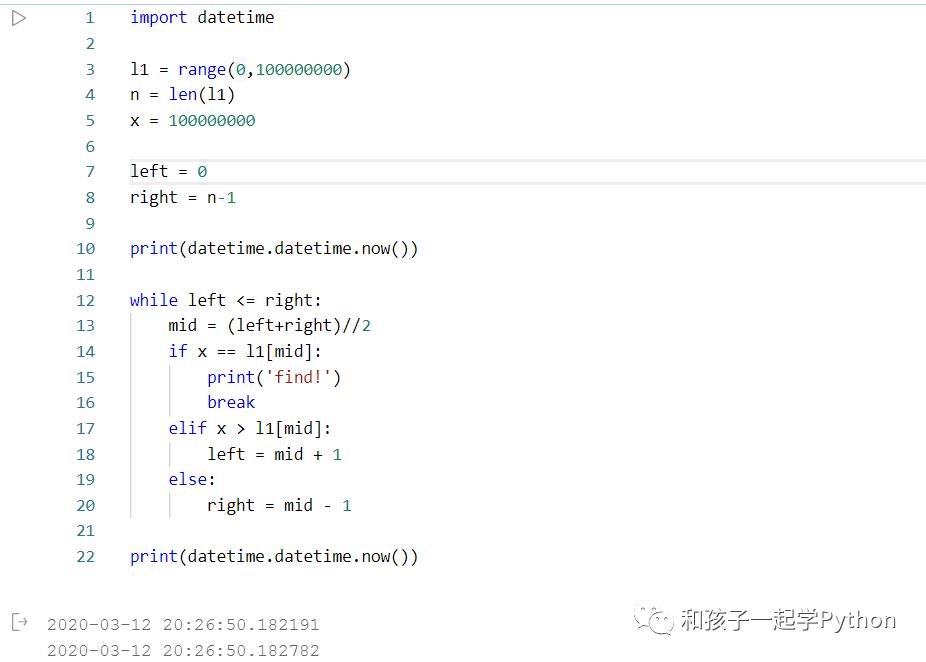
    使用“二分查找”，只用了 0.0006 秒不到！

 

选择排序

    现实生活中，数据往往是无序的。而我们又时时刻刻都在查找。

    所以，想办法将无序的数据变得有序，从而可以使用“二分查找”就变得非常重要！

    给定一个如下的无序列表，如何对它进行排序呢？

import random
list1 = random.sample(range(0,100),9)

    问题看上去很简单。

    先找到最小的，放到第1位

    再找到次小的，放到第2位

    ……

    这种排序方法被称为“选择排序”。

    虽然选择排序看上去很容易理解，并且网上还有无数的解释教程，甚至还做了像下面这样形象生动的gif动画。

    

    但初学者依然很难写出正确的程序。一个重要的原因是不能真正理解电脑的工作方式。

    

    如果有条件的话，可以找9个盒子，装入9个不同的数字纸片。

    上一篇介绍过，这种方式非常接近列表在电脑里的真实状态。

    然后实际动手模拟选择排序的过程，这种方式将非常有助于理解电脑的工作方式，理解选择排序的程序代码。

    下一篇，我们将详细介绍这个过程，及对应的程序。

    

    在模拟过程中，要注意的是：

• 只有拉开盒子，才能看到盒子里的数字。并且去拉另一个盒子前，要把当前盒子重新关上。

• 不能挪动盒子，只能把盒子里的数字纸片拿出来交换位置。
  

    往期文章 https://dwz.cn/gBg1UPmk

    或关注公众号，点“原创文章”

扫描二维码

获取更多精彩

少儿编程