搞定所有的二分查找

Posted 2021-04-10 做个精致男孩

        乍一看二分查找其实挺简单的，思想也简单。感觉很多问题都这样，自己觉得很简单，做到题目一直出bug，最后没能在规定的时间内做出来，然后自己抱怨。归根到底是眼高手低，基础不扎实。

        最常见的二分查找是这样的：

def biSearch(arr,left,right,target):    while(left<=right):         mid = left + (right-left)//2         if arr[mid] == target:          return mid         if arr[mid] < target:             left = mid+1         else:          right = mid-1     # 跳出循环则就是找不到这个元素     return -1

        以前觉得写到这就差不多了。二分法基本也就这样了。

        但是这个写法的弊端还是挺多的。

优点：

        找到目标元素直接返回。想法直接。

缺点：

•  如果数组内多个元素重复，找到左边界和右边界不容易。
  

•  退出循环的时候，left和right的值不相等，得思考退出时的left和right究竟是什么。

        综上，这种方法很多情况下并不推荐。

        底下有另一种思路来写二分法。排除的思想。

        每次排除一半的不符合要求的元素。再从剩下的另一半中如此往复。最后会返回一个元素。再判断这个元素是否符合要求。代码如下：

def biSearch(arr,left,right,target):    while(left<right): mid = left + (right-left)//2         # 排除一半的元素         if arr[mid] < target:         # 否则目标元素在右半边数组中(不包含mid)             left = mid+1         else:         # 否则target就在左半边数组中(包含mid)          right = mid              # 跳出循环则就是left == right,还要判断这个元素是否为目标元素     return arr[left]==target 

优点：

• 代码简洁明了。只有两种可能，target在左边或者target在右边。

• 思路明确，每次排除一半，最后只会剩下一个再判断。

• 最重要的其实还是数组有重复元素时候找左右边界方便。

  
  

底下举几个例子层层递进讲解。

Example 1:

这是最最简单最最基础的二分查找了。

def search(nums,target): left = 0        right = len(nums)-1        while(left<right):            mid = left+(right-left)//2            # 每次排除一半,如果数组左边不满足则舍弃左边 if nums[mid]<target:            # 说明目标值在右边，nums[mid]也不是目标值，所以left=mid+1 left = mid+1 else:            # 说明目标值在左边，nums[mid]可能为在mid,所以要包括mid right = mid return left if nums[left]==target else -1

Example 2:

这题是有重复元素的序数组查找左边界和右边界。如果是之前传统的二分查找写法不太好找边界。

其实找左边界就是之前代码的写法，参考Example1：

                                            

        仔细品品，重点在 if nums[mid]<target  这句判断，如果nums[mid]恰好为target，那么会排除右边的一半。边界不断地向左收紧，比如最后只有[8,8]元素了，那么最后边界会往左边的8缩进。退出循环时left = right = 左边界。

        写到这边可以想想右边界怎么找，其实思想也是一样的。就是不断地排除左边的数组，边界往右边缩进。判断改成，if nums[mid]<=target 则不断地排除左边的，边界往右边走。

 

def getRightBoundary(nums,target): left = 0 right = len(nums)-1 print('Find Right Boundary:')    while(left<right):
 mid = left+(right-left)//2        if (nums[mid]<=target): left = mid else: right = mid-1 return right if nums[left]==target else -1

至此，以后有序数组的二分查找边界应该是小case。

Example3:

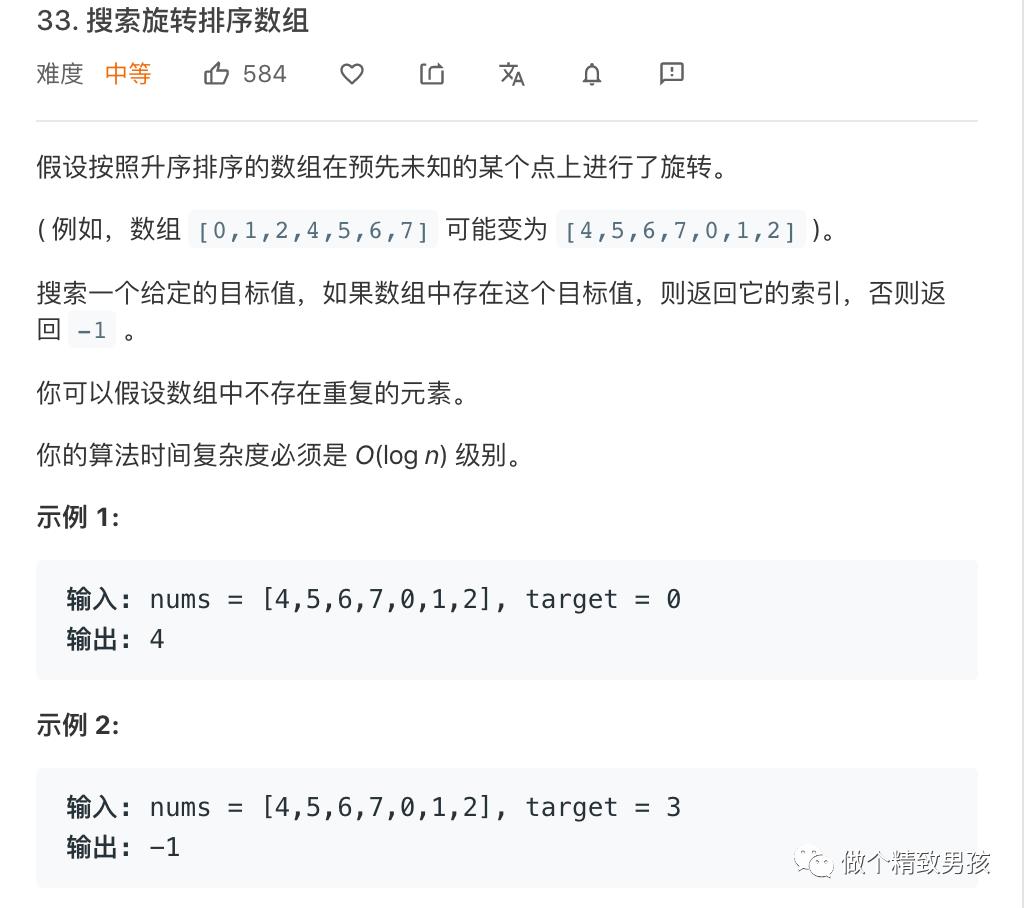
二分查找不一定只能用在有序数组上，也可以运用在部分有序数组上，比如这题。遇到这题第一反应应该也是二分查找。但是这边的nums[mid]不一定是中位数。时刻记住二分查找的思想是排除一半。

此时有两种思路。

• nums[mid]和nums[left]比看能不能去除一半不符合的。

• nums[mid]和nums[right]比看能不能去除一半不符合的。

  
  

这两种思路都是可以的。

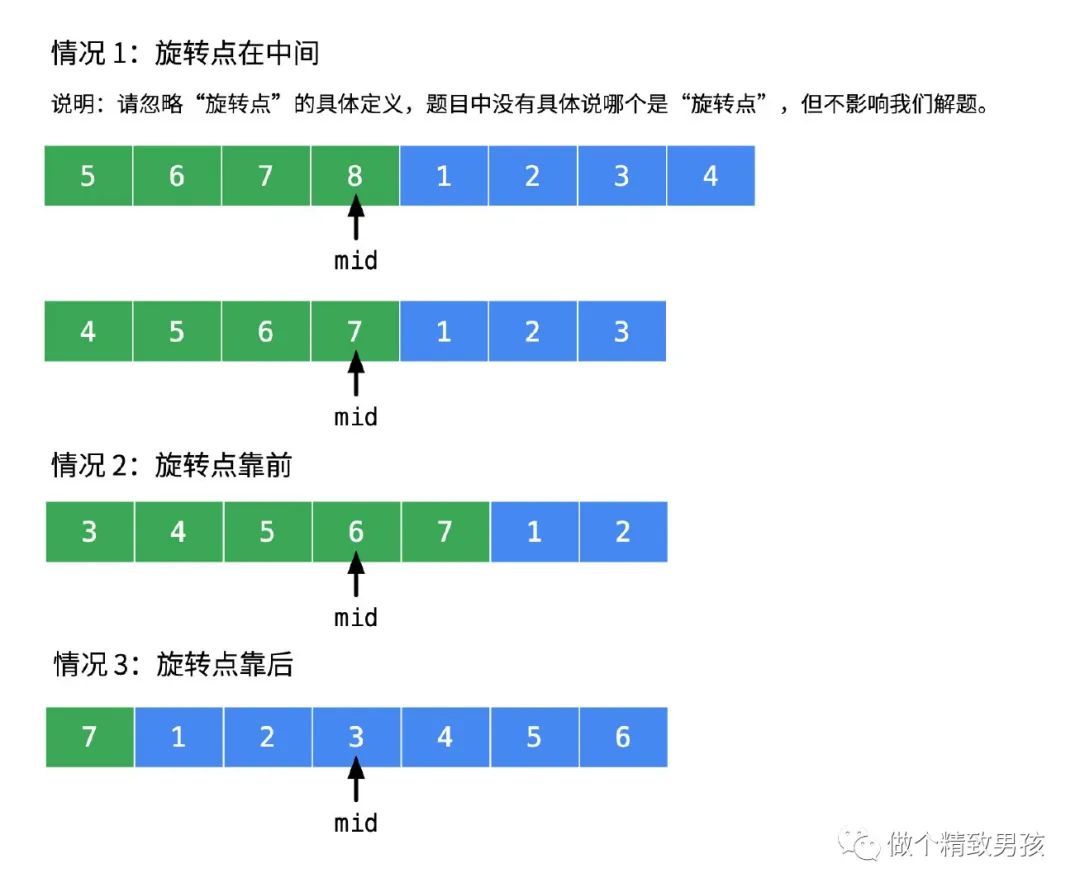
(图片参考力扣 liweiwei1439。)

可以看到不管旋转点在哪边，只要判断mid和left或者right的值就知道，mid落在哪边的有序数组中。

我们以第二种思路为例子。

        如果nums[mid]<nums[right]:说明nums[mid:right]都是有序数组的，如果target在这其中二分查找即可。（nums[mid]<=target<=nums[right]）。如果target在左边的无序数组中，只能慢慢缩小边界查找，每次右边界减少1进行试探。即right = mid-1。

        同理如果nums[mid]>nums[right]:说明nums[left:mid]有序，如果target在左半边，二分查找即可。(nums[left]<=target<=nums[mid])。如果target在右边的无序数组中，只能左边界+1去试探，即left = mid+1。

def search(self, nums: List[int], target: int) -> int: if not nums : return -1 left = 0 right = len(nums)-1 while(left<right):            mid = left+(right-left+1)//2 if nums[mid]<nums[right]: if nums[mid]<=target<=nums[right]: left = mid else:                    right -= 1 elif nums[mid]>nums[right]: if nums[left]<=target<=nums[mid]: right = mid else: left = mid+1 else:                # 这边边界要好好调试代码，有可能陷入死循环，                # 打印出left，right，mid就知道问题在哪了。 if nums[right]==target: return right right -= 1 return left if nums[left]==target else -1

(如果数组中有重复元素，也是这么解决的并无区别)

Example 4:

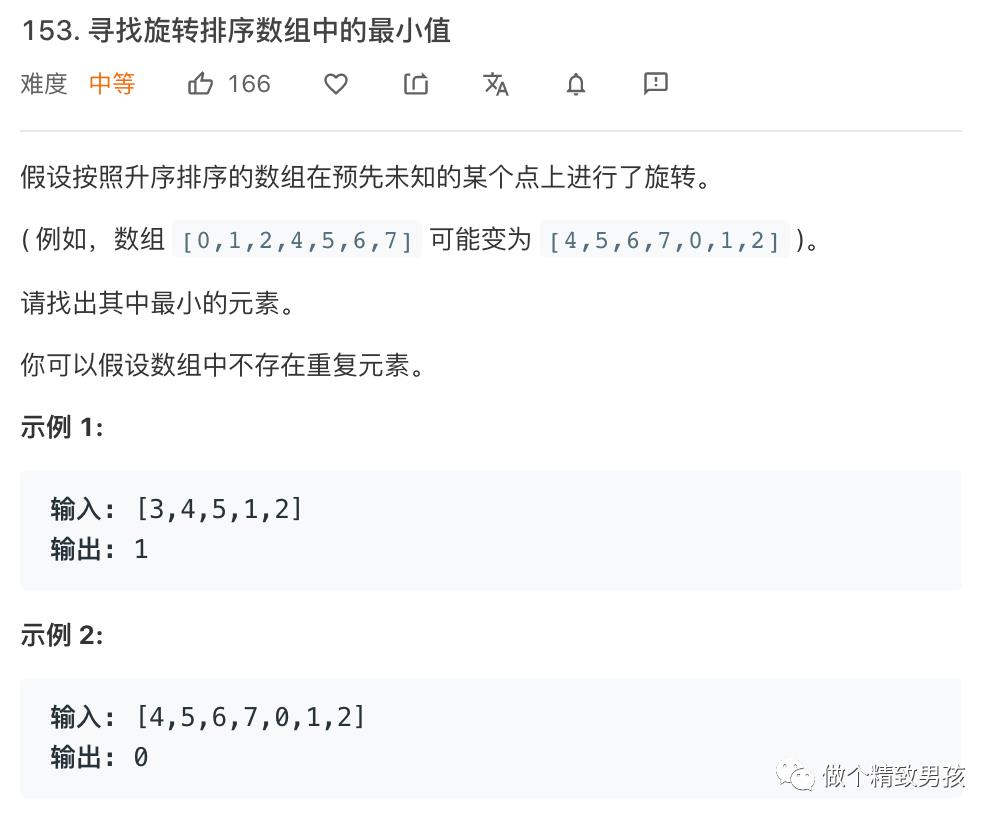
再来看这种题。。中等难度。1分钟AC了。理解了思路原理，统统很easy。所以好好体会挖掘一题，举一反三胜过盲目做十道题。

简单说下思路，如果左边有序，则最小值一定在右边。如果右边有序则最小值一定在左边。就是这么简单。。

def findMin(self, nums: List[int]) -> int: left = 0 right = len(nums)-1 while(left<right): mid = left+(right-left)//2 if nums[mid]<nums[right]: right = mid else: left = mid+1 return nums[left]

Example5：

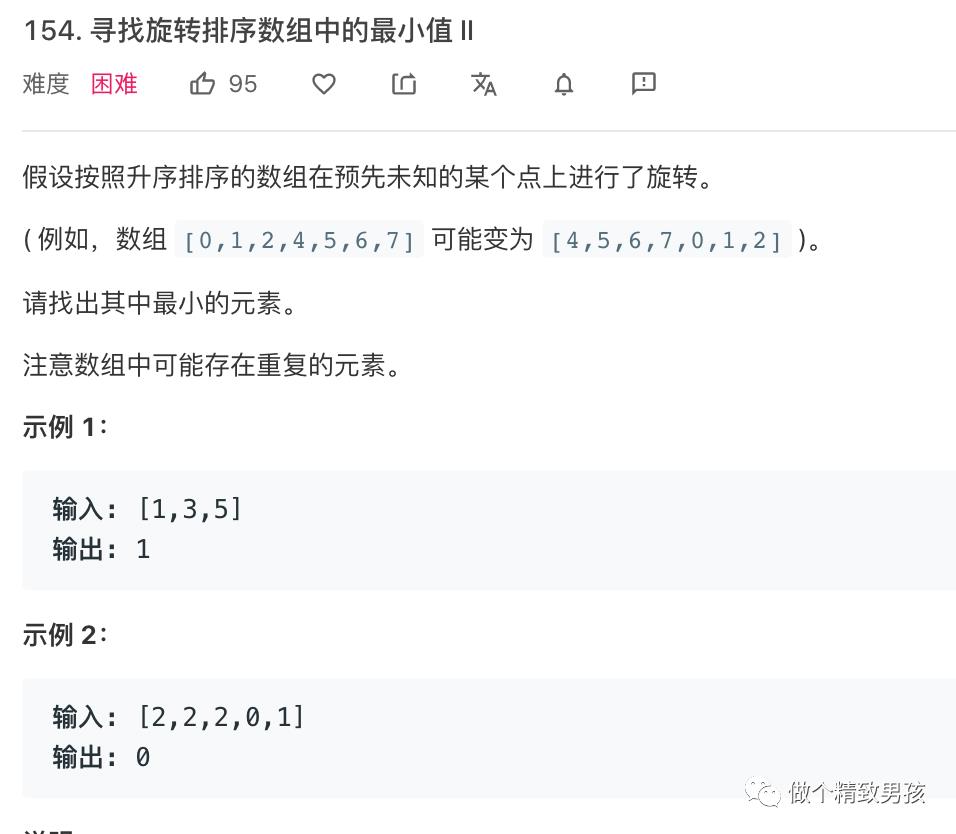
话不多说，这种困难的题也轻松一分钟AC。。重复元素唯一要考虑的就是nums[mid]和nums[right]相等的时候，这时候不知道右边数组是不是递增的，此时让right-=1，右边界向左收缩，直到能判断右边数组到底是不是递增的即可。

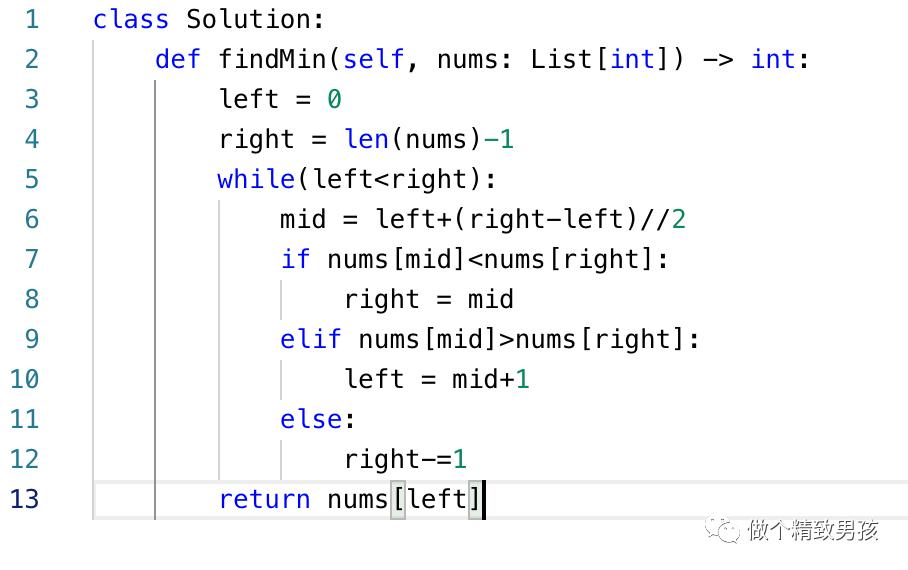
Example6:

        下面这题有一点难度，运用到了贪心算法+二分查找。其实这些算法拆开来都并不是特别难。只是要灵活运用，还是要多做题。比如遇到有序数组要插入，肯定要用二分查找，线性查找就是二五仔。

        这题可以用dp做时间复杂度是O(n^2)这里就不讲了。主要讲下贪心+二分。时间复杂度是O(nlogn)。每个元素插入的复杂度是logn，一共n个元素。

        这边我们维护一个tail数组。对于任意长度i，tail[0:i]代表长度为i且结尾最小的上升子序列。例如i=2代表长度为2，且结尾最小的序列，这样的序列有很多例如[2,5],[2,3],[5,7],[3,7]等等，但是相同长度的子序列，最后一个数肯定是越小越好的。题中就是tail[0:2]就是[2,3]，如果i=3呢，tail就是[2,3,7]。

        那如何维护一个tail呢。

• 当新进来的num[i]>tail[-1],说明当前数字加进来一定可以构成更长的子序列，直接加入数组。

• 如果nums[i] 已经在tail中了就不需要考虑了，直接跳过。

• 如果nums[i]<tail[-1]时，替换掉tail中第一个大于nums[i]的数字，例如，此时的tail为[2,5]，nums[i]=3，在tail中找到第一个大于3的数字，是5，则替换掉5，tail变为[2,3]。

所以我们维护的tail一直是递增的序列，每次新进来的数字要替换掉第一个大于它的数。有序加插入，这显然是二分查找来维护tail。

        至此，以后遇到二分查找的问题，应该5分钟内AC掉。。掌握了思路，二分查找还是非常简单的。主要就是细节比较麻烦，还是可能出问题，多调试，多总结。

       祝进步。