二分查找求解
Posted 力扣日记
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二分查找求解相关的知识,希望对你有一定的参考价值。
给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。
请你找出这两个正序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。你可以假设 nums1 和 nums2 不会同时为空。
题解:
1.两个正序数组
2.两个正序数组的中位数即两个数组合并后的有序序列中位数
3.时间复杂度为 O(log(m + n))
4.nums1 和 nums2 不会同时为空
示例 1:
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
解题思路:
选出两个序列中较短数组进行遍历标志,尽可能减少运算次数
左指针在短数组中走,注意左指针下标不超过短数组长度-1位置
右指针在长数组中,从后向前走,记录一个合并总长度
一前一后向内走对应起来,像是回文判断一样,这里换成数值比较找到中间数,此时指针位于此,总长度为奇数则俩指针都指向该数;为偶数,则左右指针指向中间两数
再进一步判断是奇长度还是偶长度返回对应的中位数
C/C++题解:
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int n1 = nums1.size();
int n2 = nums2.size();
if(n1 > n2)
return findMedianSortedArrays(nums2, nums1);//前者为短数组
int L = 0, R = n1 - 1, m1, m2;//在短数组中遍历
int k = (n1 + n2 + 1) / 2; //+1两者合并后偶奇序列中间下标值相同
while(L <= R){
m1 = L + (R - L) / 2; //左指针从左向右走
m2 = k - m1; //对应右指针从右向左
if(nums1[m1] < nums2[m2 - 1]) //比较两指针对应数
L = m1 + 1;//左指针小,则左指针向后移
else //右指针小则中位数在左指针那边
R = m1 - 1;//移动右指针
} //左右指针相等
m1 = L; //奇序列即此时位于正中间下标
m2 = k - m1; //偶序列此时下标为中间第二个数
int c1 = max(m1 <= 0 ? INT_MIN : nums1[m1-1]
, m2 <= 0 ? INT_MIN : nums2[m2-1]);
//奇长度序列中位数为两序列较长序列中间位置相较大数
if( (n1 + n2)%2 == 1) //两者数组长度和为奇数
return c1;
//偶数在是两序列较长序列中间下一位置较小值且大于c1
int c2 = min(m1 >= n1 ? INT_MAX : nums1[m1]
, m2 >= n2 ? INT_MAX : nums2[m2]);
return (c1 + c2)/2.0;}}; //取中间两数平均
Debug结果:
Java题解:
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int n1 = nums1.length;
int n2 = nums2.length;
if(n1 > n2)
return findMedianSortedArrays(nums2, nums1);//前者为短数组
int L = 0, R = n1 - 1, m1, m2;//在短数组中遍历
int k = (n1 + n2 + 1) / 2; //+1两者合并后偶奇序列中间下标值相同
while(L <= R){
m1 = L + (R - L) / 2; //左指针从左向右走
m2 = k - m1; //对应右指针从右向左
if(nums1[m1] < nums2[m2 - 1]) //比较两指针对应数
L = m1 + 1;//左指针小,则左指针向后移
else //右指针小则中位数在左指针那边
R = m1 - 1;//移动右指针
} //左右指针相等
m1 = L; //奇序列即此时位于正中间下标
m2 = k - m1; //偶序列此时下标为中间第二个数
int c1 = Math.max(m1 <= 0 ? Integer.MIN_VALUE : nums1[m1-1]
, m2 <= 0 ? Integer.MIN_VALUE : nums2[m2-1]);
//奇长度序列中位数为两序列较长序列中间位置相较大数
if( (n1 + n2)%2 == 1) //两者数组长度和为奇数
return c1;
//偶数在是两序列较长序列中间下一位置较小值且大于c1
int c2 = Math.min(m1 >= n1 ? Integer.MAX_VALUE : nums1[m1]
, m2 >= n2 ? Integer.MAX_VALUE : nums2[m2]);
return (c1 + c2)/2.0; }}//取中间两数平均
Debug结果:
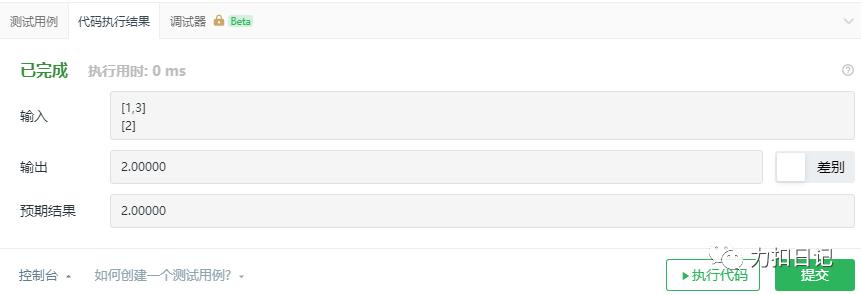
Python题解:
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
""":type nums1: List[int]:type nums2: List[int]
:rtype: float"""
n1 = len(nums1)
n2 = len(nums2)
if(n1 > n2):
return self.findMedianSortedArrays(nums2, nums1) #前者为短数组
L = 0
R = n1 - 1 #在短数组中遍历
k = (n1 + n2 + 1) / 2 #+1两者合并后偶奇序列中间下标值相同
while L <= R:
m1 = L + (R - L) / 2 #左指针从左向右走
m2 = k - m1 #对应右指针从右向左
if(nums1[m1] < nums2[m2 - 1]): #比较两指针对应数
L = m1 + 1 #左指针小,则左指针向后移
else: #右指针小则中位数在左指针那边
R = m1 - 1 #移动右指针
#左右指针相等
m1 = L #奇序列即此时位于正中间下标
m2 = k - m1 #偶序列此时下标为中间第二个数
if m1 <= 0:
a = -sys.maxint
else:
a = nums1[m1-1]
if m2 <= 0:
b = -sys.maxint
else:
b = nums2[m2-1]
c1 = max(a, b);
#奇长度序列中位数为两序列较长序列中间位置相较大数
if( (n1 + n2)%2 == 1): #两者数组长度和为奇数
return c1
#偶数在是两序列较长序列中间下一位置较小值且大于c1
if m1 >= n1:
a = sys.maxint
else:
a = nums1[m1]
if m2 >= n2:
b = sys.maxint
else:
b = nums2[m2]
c2 = min(a, b)
return (c1 + c2)/2.0 #取中间两数平均
Debug结果:
例题来自力扣网https://leetcode-cn.com/
欢迎评论后台留言交流~
以上是关于二分查找求解的主要内容,如果未能解决你的问题,请参考以下文章