基本的查找-顺序查找和二分查找

Posted 2021-04-09 ThinkingLog

今天开始每天说一点查找算法。查找顾名思义，就是在一堆数据里面找到自己想要的那个。对于这个任务，最开始谁都可以想到的方法就是把东西排查排，一个一个的找过去。这就是顺序查找了。

顺序查找非常朴素，特别好理解，实现起来也非常容易，但就有一个问题，慢。

之前有个段子，说生物专业的博士生形容自己的工作，就像是拿了一大串钥匙，一个一个试能不能打开前面这扇门。如果运气好，在前几次尝试里面就恰巧找到了钥匙，那就可以快速毕业，立刻在学术界打开一片天，成为颇有影响的年轻学者。如果运气不好，打开这扇门的钥匙在这一串钥匙中的最后的位置，那别说毕业了，学术生涯可能都完蛋了。

那这个生物专业的博士生无奈使用的就是顺序查找，运气好第一个就找到了，运气不好那就是这个序列里面有多少数据，就要尝试多少次，非常的无奈。如果这个序列有1亿条数据，那最坏的结果可能就是要找1亿次，这种速度肯定会让人崩溃的。

那就需要进行查找优化，那么最简单的查找优化，就是二分查找。

顺序查找中我们不要求被查找的序列是有顺序的，无论你怎么排序，都得一个一个的找。但这种乱序中，肯定无法提升查找速度。那把被查找序列排个序，就有可以提升的空间了。二分查找就是在有序列表中，进行查找的方法。

二分查找是一种不断缩小搜索范围的思路。首先我们先找到所有数据的中点，然后和查找目标做比较，如果目标大于中点，我们就再来比较序列的右半边。再取右半边序列的中点，然后再用同样的方式比较。直到某一次取的中点等于目标值，那就完成了查找。

举个例子说明一下。

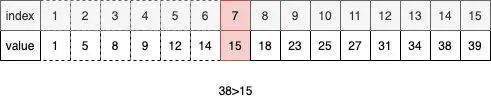
这是一个已经排好序的列表，我们想要查找38这个值。

1. 取序列的中点：序列中是有15个数字，那么我们可以定义中点为 结果的整数部分，中点索引为7，对应的数据为15。

   

2. 比较目标和中点：我们的目标是38，中点为15，则38大于15。所以我们下一次只看中点右边的序列。

   

3. 取右半边的中点：因为上一步我们只保留了序列的右半边，所以起始索引也就发生了变化。右半边的中点为 的整数部分，中点的索引为11，值为27。

   

4. 比较右半边中点和目标值：再比较一下新的中点和目标值，38还是大于27，所以继续保留右半边的序列。

   

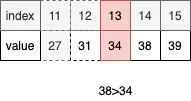
5. 再取右半边的中点，比较中点和目标的大小。中点的索引为13，值为34。再和目标值38比较，我们还是要取右边部分的序列。

   

6. 重复上面的步骤，取序列中点，比较中点和目标值。这次的中点索引为14，值为38。做一下比较刚好中点值和目标值相等。于是我们找到了最终目标值的位置，查找结束。

   

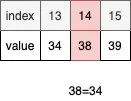
我们看一下这个例子中，二分查找法总共进行了4次比较，完成了最终的查找。而如果是顺序查找，则需要14次。这么看来还是节省了不少时间的。如果比较系统的来看这两个算法的查找复杂度，顺序查找是 ，二分查找是 。

简单的实现

# 顺序查找def search_sequence(l, search_v):

 for i in range(len(l)): if l[i] == search_v: return i return None  # 二分查找 def search_binary(l, search_v): low = 0 high = len(l) def search_b_recursion(low,high,l,search_v): if low == high: return "Not in list" mid = low+(high-low)//2 if l[mid] == search_v: return mid else:
 if l[mid] < search_v: low = mid + 1 else: high = mid - 1
 return search_b_recursion(low,high,l,search_v)
 return search_b_recursion(low,high,l,search_v)

END

   图片：网络（侵删）