算法系列二分查找的“变形记”

Posted 2021-04-09 百家分享汇

    你好！我是不务正业的店小二。今天是周日，很高兴我们再次相遇；眨眼间距离上次分享已经过去半年，不由感叹光阴似箭，岁月如梭。今天我和你分享二分查找算法注意事项及其常见的几种“变形”实现。

二分查找的高效及其局限性

    无处不在的二分查找，经常回到家妈妈都说她买了一件衣服，猜猜多少钱。她或许给你一个区间范围，让你猜。她说贵了你就往小猜，便宜了就往大猜。这就是简单的二分查找算法。

    二分查找算法是基于有序的数据集合，其思想有点像分而治之。在不需要额外消耗内存空间的情况下，其时间复杂度可以说非常快，只需要O(logn)。至于是怎么个计算过程，有兴趣的朋友可以先去学习下，改天我再额外拿出来给大家分享。

    递归可不递归都能实现二分查找算法，不递归的话那就是用while循环即可实现，先抛砖引玉我们的案例就是采用while循环实现，有兴趣的朋友可以自己用递归的方式试试，或许你会踩坑。递归使用不当会带来重复计算，会带来堆栈溢出的情况，递归的深度。

    我们来聊聊二分查找的局限性。首先，二分查找依赖的是顺序表结构，即数组。链表能否作为二分查找的数据结构呢？显然不能，因为二分查找算法要按照下标随机访问元素。链表的随机访问时间复杂度是O(n)，而数组只需要O(1)。其次，二分查找针对的是有序的数据。这点好理解，数组必须是有序的，否则怎么能不断缩小查找范围。但是如果频繁插入、删除操作的数组是不适合进行二分查找的。再次，通常情况数据量太小也不适合使用二分查找。比如一个小于20左右的数组采用二分查找和顺序遍历两者的性能优势并不显著。当然，如果对于字符串数组如果长度超过300以上，则使用二分查找可减少比对次数，以此减少性能的损耗。最后，数据量太大也不适合二分查找。主要原因是数组的结构是要连续的内存空间，如果一个数组是1GB、2GB。此时内存剩余有1GB或2GB，但是内存空间是零散，则无法连续存放如此之大的数据。二分查找也就无用武之地了。

    示例代码

/** * 普通二分查找，找到即退出 * * @param arr 数组 * @param n 数组长度 * @param value 待查值 * @return */ public static int binarySearch_Nornal(int[] arr, int n, int value) {     int low = 0;     int high = n - 1;     while (low <= high) {         int mid = low + ((high - low) >> 1);         if (arr[mid] > value) {             high = mid - 1;         } else if (arr[mid] < value) {             low = mid + 1;         } else if (arr[mid] == value) {             return mid;         }     }     return -1; }

变形一：查找第一个值等于给定值的元素

    我们要查找到上图的target指向的元素8，用二分查找算法该如何实现呢？如果用上面的实例代码，执行后你会发现输出的下标是7。尽管a[7]的值也是8，但是并不是我们所想要的第一个等于8的元素，应该是要a[5]才对。还是老样子，直接看实例代码。

public static int binarySearch_equalFirstValue(int[] arr, int n, int value) {   int low = 0;   int high = n - 1;   while (low <= high) {       int mid = low + ((high - low) >> 1);       if (arr[mid] > value) {           high = mid - 1;       } else if (arr[mid] < value) {           low = mid + 1;       } else {           if ((mid == 0) || (arr[mid - 1] != value))               return mid;           else               high = mid - 1;       }   }   return -1;}

我们看三个条件语句，大于、小于、等于。我们一起来看看11行。如果mid等于0，那就是这个元素就是数组的第一个元素，那它肯定就是结果值；如果mid不等于0，但a[mid】的前一个元素a[mid -1]不等于目标元素value，那也说明a[mid]就是我们要找的第一个值等于给定值的元素；否则，我们要找的元素就在[low,mid-1]区间。

 变形二：查找最后一个值等于给定值的元素

    这一次我们反过来，查找的是最后一个值等于给定值的元素，我们假定给定值还是8。那我们又该如何实现呢？如果你也跟着我一样敲了上面的实例代码，而且你也掌握了，那这个问题解决起来就会游刃有余。

public static int binarySearch_equalLasterValue(int[] arr, int n, int value) { int low = 0; int high = n - 1; while (low <= high) { int mid = low + ((high - low) >> 1); if (arr[mid] > value) { high = mid - 1; } else if (arr[mid] < value) { low = mid + 1; } else { if ((mid == n - 1) || (arr[mid + 1] != value)) return mid; else low = mid + 1; } } return -1;}

还是关注第11行的变化，以及14行。如果没有满足11行，则我们执行的14行，其实就是在往高的区间走[mid+1,high]。

变形三：查找第一个大于等于给定值的元素

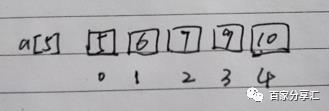
    现在我们再来看第三种变形情况。如上图所示数组，我们要查询第一个大于或等于8的元素，那就是9，坐标是a[3]。我们要如何实现呢？请和我一起看实例代码。

public static int binarySearch_GreaterThanOrEqualToValue(int[] arr, int n, int value) { int low = 0; int high = n - 1; while (low <= high) { int mid = low + ((high - low) >> 1); if (arr[mid] >= value) { if ((mid == 0) || (arr[mid - 1] < value)) return mid; else high = mid - 1; } else { low = mid + 1; } } return -1;}

    如果arr[mid]小于要查找的值value，那么该值所在区间就是[mid+1,high]，即更新low = mid +1。对于arr[mid]大于等于给定值value的情况，我们则先要看看a[mid]是不是就是我们要的结果；又或者如果arr[mid]的前一个元素是否小于给定值value，如果是则结果也是我们想要的；否则在区间[low,mid-1]查找。

    我们来看最后一种变体。

变形四：查找最后一个小于等于给定值的元素

    

    我们要查找小于等于7的元素，从图上很直观的看到要查找的就是6。根据前面的代码，我们稍作修改就能达到目的。

public static int binarySearch_LessThanOrEqualToValue(int[] arr, int n, int value) { int low = 0; int high = n - 1; while (low <= high) { int mid = low + ((high - low) >> 1); if (arr[mid] > value) { high = mid - 1; } else { if ((mid == n - 1) || (arr[mid + 1] > value)) return mid; else low = mid + 1; } }
 return -1;}

附加

    上文的实例中，第5行我们通常的写法更多的是mid=(low+high)/2。这里使用移位处理，一是避免low+high因两数值过大相加会导致溢出，二是计算机移位的处理相比除法运算要快很多。

总结

    本文篇幅比较长，主要是简单的介绍了二分查找算法的优势以及局限性，主要是无需额外的内存空间消耗，以及查找效率高，局限性在于适合用在有序的，且数据量适中数组中。随后给你分享了二分查找算法的4种变形情况，也包含了实例代码。希望你能动手敲一敲！

思考和讨论

    1、文中说到的二分查找算法的时间复杂度是O(logn)，这是怎么计算来的呢？

    2、如果数组是有序循环数组，那怎么实现查找给定值呢？

欢迎留言与我分享和指正！也欢迎你把这篇文章分享给你的朋友或同事，一起交流。

感谢您的阅读，我们下节再见！