介绍一下二叉树期权定价原理

Posted 2021-04-09 市川新田三丁目

本文中的案例及大部分内容来自于佛吉尼亚大学Darden商学院教授Robert M. Conroy

的文章《BINOMIAL OPTION PRICING》。

在各种期权定价理论中，二叉树期权定价模型称得上是既简单又有效。其他的定价模型如BLACK-SCHOLES模型等都需要晦涩难懂的计算，而二叉树期权定价模型的计算过程就容易得多。

二叉树模型的理论基础是假设在金融市场上没有任何套利空间，也就是任何无风险的资产带来的都是无风险的回报率，一分钱也不花却想获得正回报的可能性是不存在的。

二叉树期权定价模型

假设我们持仓1股的某只股票，单位股价为100美元，一个月过后，股价有两种走法：上涨的情况下涨到110，或下跌的情况下跌到90，没有其他的可能性。

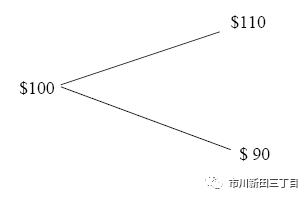
假设以该股票为标的物的看涨期权的行权价@100美元，期限为1个月。1个月后期权到期日当天，如果股价升至110美元，那么看涨期权的期权费将等于10美元；如果股价跌至90美元，那么期权费将归于0。该看涨期权一个月后的损益情况见下图：

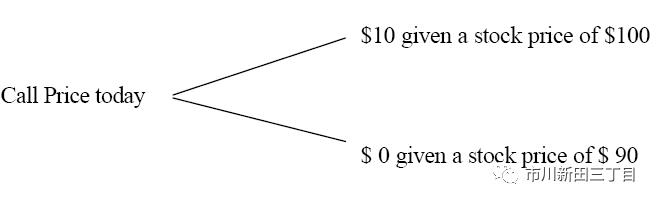
问题来了：今天，这个看涨期权的期权费应该值多少钱？

假设我们今天做一笔组合交易，

1）买入0.5股该股票，股价为100，股票投资0.5*100=50美元

2）同时卖出以该股票为标的物的看涨期权，行权价@100，标的股票的数量为1股，期权的到期期限为1个月。

由于卖出看涨期权可以赚取期权费，因此这笔投资的初始金额=

                50美元-看涨期权当前的期权费

1个月后期权到期，投资组合的损益状况有两种：

1）股价升至110美元，此时0.5股的股价=0.5*110=55美元，但是卖出看涨期权将带来10美元的损失（因看涨期权的买家届时会因为有利可图而要求行权，而110的市场价与100的行权价之间的10美元差价就是期权买家的利润，而期权的卖家由于必须从市场上按照110的价格买进一股股票并按照100的价格交割给期权的买家而实质性的遭受了10美元的损失），投资组合的总收益=55-10=45美元；

2）股价跌至90美元，持仓的0.5股此时价值=0.5*90=45美元，但是空仓的看涨期权此时的价值归于0，投资组合的总收益=45-0=45美元。

投资组合的损益状况如下：

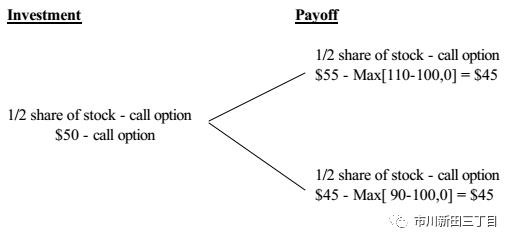
通过以上的分析可知，买入50%仓位的某股票+卖出100%仓位的看涨期权的组合交易就形成了一个无风险的投资仓位，不管1个月后股价如何表现，这笔组合交易最后的价值都是45美元。

假设该交易没有任何套利空间，那么投资者赚的就是无风险收益。因此，50美元-看涨期权期权费的初始投资金额就应该与1个月后获得的45美元的现值是等价的，而折现用的是这1个月的无风险利率。

根据以上推理，我们得出以下等式关系：

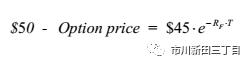
略作调整，

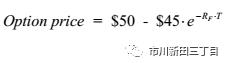
其中，R_F为无风险利率，T为以年为单位的到期期限。假设当前的年化无风险利率为6%，期权的到期期限为1个月，那么T=0.8333，代入公式计算得出，看涨期权当前的期权费为5.22美元。

以上的推理过程有一个前提假设，即必须先形成当前的投资与未来的期权组合回报之间的无风险对冲等式关系，而这个无风险对冲赚取的是无风险利率。在实践中，有两种交易策略会用到二叉树定价模型，一种是无风险对冲模式，另一种是风险中性模式。这两种做法的定价结果是一样的，下面分别进行演示。

无风险对冲模式

在上面的例子中，对冲比率，即每单位的看涨期权所相对应的股票数量，是事先给定的。下面我们来研究一下如何确定对冲比率，期权的期限还是一个月，见下图：

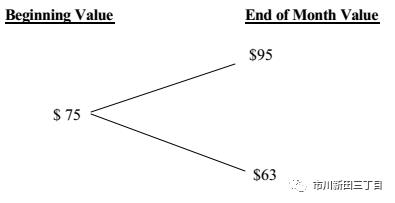
在这个例子中，当前的股价为75美元，一个月后，股价要么是95，要么是63，假设看涨期权的行权价@65，一个月后，看涨期权的损益情况见下图：

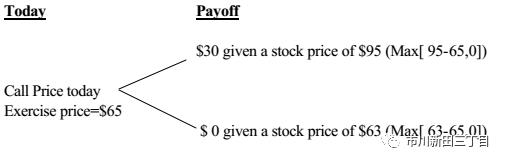
也就是一个月后，

1）如果股价涨到95，那么看涨期权的收益为95-65=30

2）如果股价跌到63，那么看涨期权的收益为63-65=-2，由于期权的价值不可能为负值，最后取值0

如果假设持仓的股票数量为H，那么前面提到的买入股票+卖出标的股票数量为1股的看张期权的组合交易的初始总投资金额=H*75美元-行权数量为1股的看涨期权的期权费，

1）如果一个月后股价为95，那么投资组合的价值为H*95-30，

2）如果一个月后股价为63，那么投资组合的价值为H*63-0，

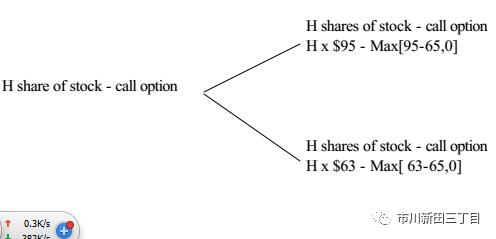
假设没有套利空间，那么这两种情境下投资组合的价值应该相等，即

H*95-30=H*65-0，而H=（30-0）/（95-65）=0.9375

由于已知H=0.9375，那么在一个月后股价为63的情况下，交易组合的价值为0.9375*63-0=59.0625；一个月后股价为95美元的情况下，组合交易的价值为0.9375*95-30=59.0625美元。就这样通过买入0.9375股的股票+卖出行权股票数量为1股的看张期权，就形成了一个无风险对冲交易，不管一个月后股价在什么水平，组合交易的价值均为59.0625美元。

因此，初始总投资金额=0.9375*75-C，C为看涨期权的期权费，假设没有任何套利空间，0.9375*75-C就应该等于将于一个月后收到的59.0625用无风险利率贴现到今天的现值。

还是假设年化无风险利率为6%，期权的到期期限为一个月，即T=1/12=0.8333，那么今天看涨期权的期权费就等于11.54美元，计算过程如下：

前面谈的是在期权有效期之内股票价格只有一次变动的情况下二叉树模型的应用，如果在期权有效期之内股票价格有多个变动的可能性，应如何利用二叉树模型为期权定价？

假设在一个月内股价变动的次数不是一次，而是每两周变动一次，那么通过下图可以看出，一个月的期权有效期被分成了前后两个阶段，在一个月后，股价有三种变动的可能性，本例中，初始股价假设为100：

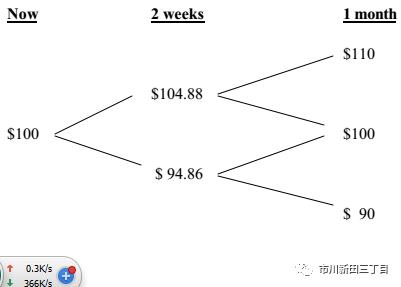
问题还是一样：将于一个月后到期的行权价@100的看涨期权今天的期权费应该是多少？

其实，这个问题并不比前面的问题难多少，解题的关键是从经历了多个阶段后股价最终的多个变化结果向前回溯，一直细分到最简单的单阶段两种演变结果的初始状态。下面开始！

先看看股价在第一个两星期的阶段过后有可能达到104.88的这种情况，从这开始，在经过第二个两星期的阶段后股价要么升至110，要么跌至100。我的问题是：假设当前的股价就是104.88，未来两个星期后到期的看涨期权的报价应该是多少？与前面的推理过程一样，第一步还是假设我们要买入H股股票，同时卖出行权数量为1股的两星期后到期的看涨期权，这个H就相当于无风险对冲交易的对冲比率。组合交易的损益情况见下图：

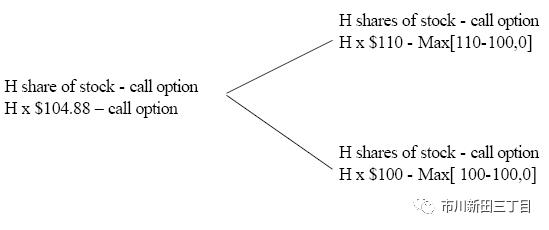
同理，

1）如果一个月后股价为110，那么投资组合的价值为H*110-10，

2）如果一个月后股价为100，那么投资组合的价值为H*100-0，

即H*110-10=H*100-0，求H=（10-0）/（110-100）=1。

这样在股价为104.88的情况下，不管两星期后股价如何变化，今天买入H股股票+卖出相当于1股的看涨期权这样一个组合交易的价值届时都会等于100*1-0=100或110*1-10=100这样一个结果。假设无风险利率为6%，由于一年有12个月，每个月有4个星期，那么到期期限2星期等于2/（12*4）=0.04167，在当前股价为104.88美元的情况下，当前的期权费应等于5.13美元，计算过程如下：

另一种情况是，在第一个两星期过后股价为94.86，在随后的两星期过后，股价要么是100，要么是90。不管哪种情况，行权价为100的看涨期权届时的价值均将归零，期权的买方因无利可图而不可能按照100的行权价来交割。掉过头来讲，在第一个两星期过后股价为94.86的情况下，看涨期权的价格也等于0。

这样我们就可以倒推到第一个两星期的阶段了，还是假设组合交易是买入H股股票+卖出相当于1股的看涨期权，其损益形态见下：

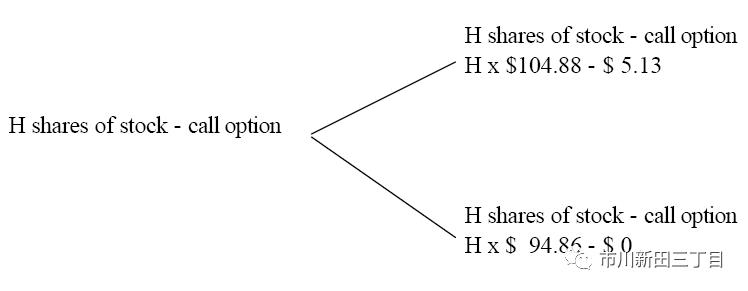
还是假设没有套利空间，由于前面已经算出来看涨期权的期权费为5.13，那么等式关系为：

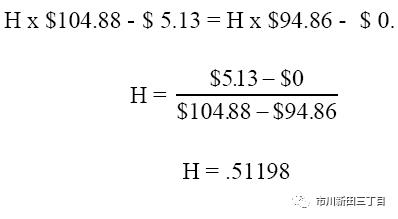
这样就算出来，在最初阶段组合交易的构成为：买入0.51198股的股票+卖出行权数量为1股的看涨期权。不管第一个两星期过后股价如何变化，届时组合交易的价值为0.51198*94.86-0=48.566或104.88*0.51198-5.13=48.566。

更具以上条件，可得出初始日看涨期权的价格为2.753美元：

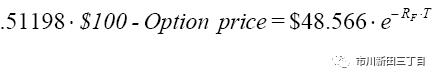
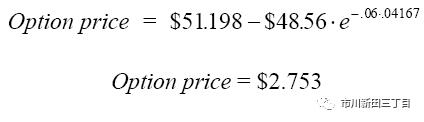
以上是无风险对冲模式的情况下，二叉树模型在期权定价中的应用。下面是风险中性模式的情况下，二叉树模型在期权定价中的应用。

风险中性模式

无风险对冲模式的情况中根本没有涉及到股价上涨的概率（被定义为P_{u）及股价下跌的概率}（被定义为P_d）这两个概念，由于股价不是上涨就是下跌，因此股价涨跌的概率加在一起P_u+P_d=1。

假设股价为75，看涨期权到期日在一个月后，一个月后股价有两种变化的可能性——涨到95或跌到63，推理过程如下：

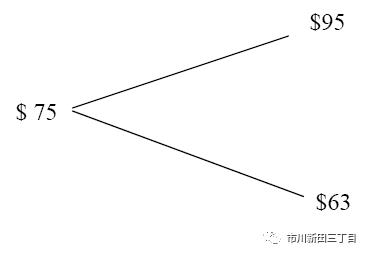
在风险中性模式下，当前的股价等于未来的股票价格按照无风险利率贴现到今天的现值。用等式关系来表示就是，

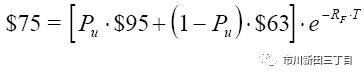
其中，R_F是无风险利率，假设为6%；而期权的到期期限T为一个月，相当于1/12=0.08333年，求股价上涨的概率P_u？

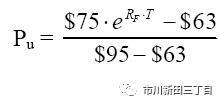
经计算，P_u=0.38675，也就是股价在一个月后涨至95的风险中性概率为38.675%，反之，股价在一个月后跌至63美元的概率等于1-0.38675=0.61325，即61.325%。

假设一个月后股价升至95，行权价@65的看涨期权带来的回报是95-65=30美元，如果届时股价跌至63，那么看涨期权的价值将归于0。按照风险中性模式来衡量，看涨期权有38.675%的可能性带来30美元的回报，有61.325%的可能性回报为0。因此在风险中性模式下，看涨期权的初始价应为11.54，计算过程如下：

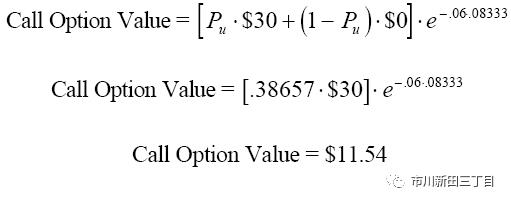
该结果与我们在无风险对冲模式下的计算结果相同。

用二叉树期权定价模型来预测未来的股价演变结果

我们将股价上涨的结果设定为u，股价下跌的结果为d

     

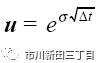
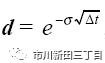
公式中期权的波动率为σ，△_t为股价波动之间的时间间隔。假设当前股价为45，波动率σ为0.20，股价波动之间的时间间隔为1个月，即△_t=1/12=0.08333，那么

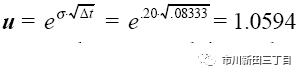
而

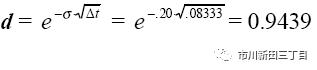
股价的变动情况如下：

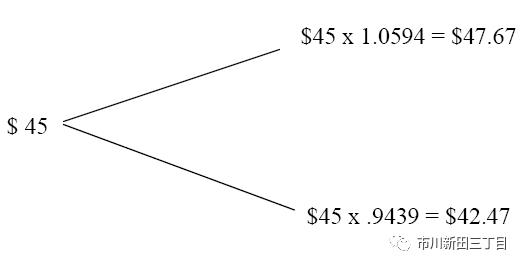
假设一个月后的结果保持不变，但是股价的变动周期调整为每两周一次，即△_t=1/（2*12）=0.04167，那么

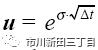
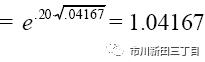
而

股价在整个月内的全部变动过程显示如下：

结论：

通过调整波动率和期限会得出不同的期权费计算结果。一般来讲BLACK-SCHOLES模型受到的重视程度更高，虽然这一现象很奇怪，但是大多数复杂的期权定价用的都是二叉树期权定价模型或其衍生出来的某些形式，二叉树模型得到广泛应用的原因就是其相对于BLACK-SCHOLES模型的灵活性。