svm原理之svm分类超平面
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了svm原理之svm分类超平面相关的知识,希望对你有一定的参考价值。
参考技术A 如图所示:什么叫线性函数呢?在一维空间里就是一个点,在二维空间里就是一条直线,三维空间里就是一个平面,可以如此想象下去,如果不关注空间的维数,这种线性函数还有一个统一的名称——超平面(Hyper Plane)!
实际上,一个线性函数是一个实值函数(即函数的值是连续的实数),而分类问题(例如这里的二元分类问题——回答一个样本属于还是不属于一个类别的问题)需要离散的输出值,例如用1表示某个样本属于类别 ,而用0表示不属于(不属于 也就意味着属于 ),这时候只需要简单的在实值函数的基础上附加一个阈值即可,通过分类函数执行时得到的值大于还是小于这个阈值来确定类别归属。例如有一个线性函数:
可以取阈值为0,这样当有一个样本 需要判别的时候,我们就看 的值。若 ,就判别为类别 ,若 ,则判别为类别 (等于的时候就拒绝判断)。此时也等价于给函数 附加一个符号函数 ,即
是真正的判别函数。
关于 这个表达式要注意三点:
实际上很容易看出来,中间那条分界线并不是唯一的,我们把它稍微旋转一下,只要不把两类数据分错,仍然可以达到上面说的效果,稍微平移一下,也可以。此时就牵涉到一个问题,对同一个问题存在多个分类函数的时候,哪一个函数更好呢?显然必须要先找一个指标来量化“好”的程度,通常使用的都是叫做“分类间隔”的指标。
下期介绍分类间隔,以及与它相关的数学知识。
SVM原理
- SVM的原理是什么?
有别于感知机,SVM在特征空间中寻找间隔最大化的分离超平面的线性分类器 - SVM为什么采用间隔最大化?
超平面可以有无穷多个,但是几何间隔最大的分离超平面是唯一的,这样的分类结果也是鲁棒的,对未知实例的泛化能力最强。 - 什么是支持向量?
对于硬间隔,支持向量就是间隔边界上的样本点
对于软间隔,支持向量就是间隔边界、间隔带内、分离超平面误分类一侧的样本点
在确定分类超平面时只有支持向量起作用,因此SVM由很少的“重要的“训练样本确定 - 为什么要将SVM的原始问题转化为对偶问题?
更容易求解(引入拉格朗日乘子,将约束优化转化为无约束优化问题)
引入核函数 (?(x)?(x)?(x)?(x)),推广到非线性分类 - 为什么要scale the inputs?(对数据进行归一化处理)
SVM对特征规模非常敏感,如果不对特征进行规范化,会导致生成的间隔带依赖于scale大的那个特征,即生成不合适的svm - 为什么SVM对缺失数据敏感?
不同于决策树,SVM没有处理缺失值的策略,它希望样本在特征空间中线性可分,所以特征空间的好坏对SVM的性能很重要 - 什么是核函数?
当样本在原始空间线性不可分时,可以将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。这个映射函数我们记为?(x)?(x)
在原始问题的对偶问题中需要求解?(x)?(y)?(x)?(y),直接计算比较困难,因此找一个核函数k(x,y)=?(x)?(y)k(x,y)=?(x)?(y),即在特征空间的内积等于它们在原始样本空间中进行核函数kk计算 - 常用的核函数有哪些,如何选择?
- RBF核/高斯核 : k(xi,xj)=exp(?||xi?xj||22σ2)k(xi,xj)=exp(?||xi?xj||22σ2),其中σσ为高斯核的带宽
- 多项式核: k(xi,xj)=(xTixj)dk(xi,xj)=(xiTxj)d,当d=1时退化为线性核
- 拉普拉斯核:k(xi,xj)=exp(?||xi?xj||2σ)k(xi,xj)=exp(?||xi?xj||2σ)
- Sigmoid核:k(xi,xj)=tanh(βxTixj+θ)k(xi,xj)=tanh(βxiTxj+θ)
- 字符串核
选择方法:经验+实验
(吴恩达)
如果Feature的数量很大,跟样本数量差不多,LR or Linear Kernel SVM
如果Feature的数量比较小,样本数量一般,不大不小,Gaussian Kernel SVM
如果Feature的数量比较小,而样本数量很多,手工添加Feature+LR or Linear Kernel SVM
- 如果一个SVM用RBF导致过拟合了,应该如何调整σσ和C的值?
RBF的外推能力随着σσ的增加而减小,相当于映射到一个低维的子空间,如果σσ很小,则可以将任意的数据线性可分,但是会产生过拟合问题,因此要增大σσ和减小CC - 为什么说SVM是结构风险最小化模型?
SVM在目标函数中有一项12||w||212||w||2,它自带正则 - SVM如何处理多分类问题?
one vs one
one vs 多,bias 较高 - SVM和LR的比较
- 样本点对模型的作用不同,SVM仅支持向量(少量样本点)而LR是全部样本点
- 损失函数不同,SVM hinge LR log
- 输出不同。 LR可以有概率值,而SVM没有
- 过拟合能力不同。 SVM 自带正则,LR要添加正则项
- 处理分类问题能力不同。 SVM 二分类,需要 one vs one or one vs all 。 LR可以直接进行多分类
- 计算复杂度。 海量数据中SVM效率较低
- 数据要求。 SVM需要先对样本进行标准化
- 能力范围。 SVM 可以用于回归
- KKT条件
- 支撑平面:和支持向量相交的平面;分割平面:支撑平面中间的平面(最优分类平面)
- SVM不是定义损失,而是定义支持向量之间的距离为目标函数
- 正则化参数对支持向量数的影响:
正则化参数越大,说明惩罚越多,则支持向量数越少 - 感知机 (判别模型)
目标函数:f(x)=sign(ωx+b)f(x)=sign(ωx+b)
损失函数:L(ω,b)=?∑xi∈Myi(ωxi+b)L(ω,b)
解决方法:随机梯度下降,每一次随机选取一个误分类点使其梯度下降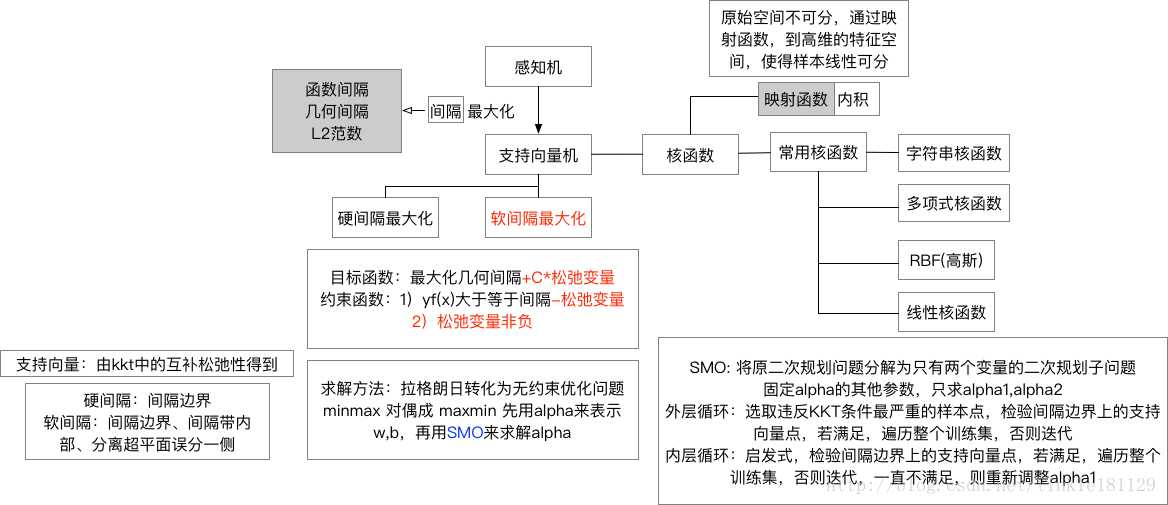
-
以上是关于svm原理之svm分类超平面的主要内容,如果未能解决你的问题,请参考以下文章