二叉树和二叉搜索树

Posted 2021-04-09 努力的yhn

二叉树和二叉搜索树——二叉树

---

二叉树

---

二叉树的定义

• 二叉树是有限个元素的集合（可以为空）。当二叉树非空时，其中一个元素称为根，余下的元素被划分为两棵二叉树，分别称为左子树和右子树。

---

二叉树的特性

• 一棵二叉树有n个元素，n>0，则它有n-1条边

• 一棵二叉树的高度为h，h>=0，它最少有h个元素，最多有2^h - 1个元素

• 一棵二叉树有n个元素，n>0，它的最大高度不会超过n

  ---

二叉树的描述

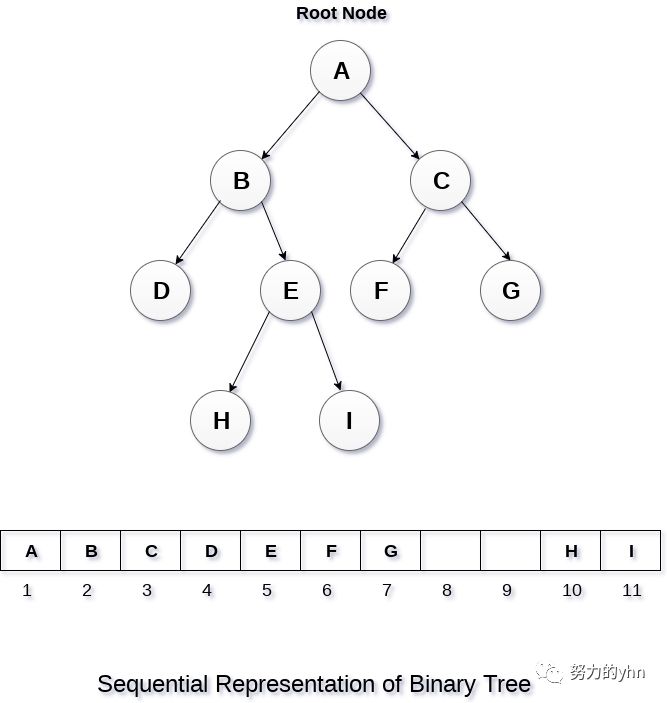
数组描述

这是存储树元素的最简单的内存分配方法，但它是一种低效的技术，因为它需要大量空间来存储树元素。

如下图所示，该二叉树存放于数组中，按照从上向下，从左到右的顺序存储在数组中。只有在缺少的元素较少时，这样的做法才是有用的。用数组存储二叉树不太常用，此处就不写关于顺序存储的二叉树了。

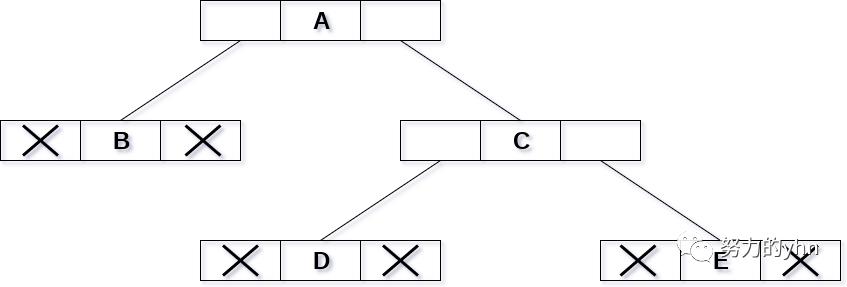
链表描述

在这种表示中，二叉树以链表的形式存储在内存中，其中节点的数量存储在非连续的内存位置，并通过像树一样继承父-子关系而链接在一起。每个节点包含三个部分:指向左节点的指针、数据元素和指向右节点的指针。每棵二叉树都有一个指向二叉树根节点的根指针。在一个空的二叉树中，根指针将指向NULL。

二叉树的数据结构

typedef int ElemType;
typedef struct TreeNode {
 struct TreeNode* left;//指向左孩子的指针
 struct TreeNode* right;//指向右孩子的指针
    ElemType data;//存储数据
}TreeNode;

二叉树的遍历

在二叉树的遍历中，用的较多的思想为递归思想，关于递归后续可能写一些关于递归思想的记录。

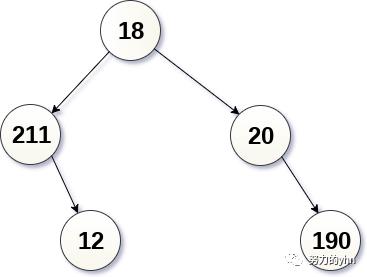
前序遍历（根→左→右）

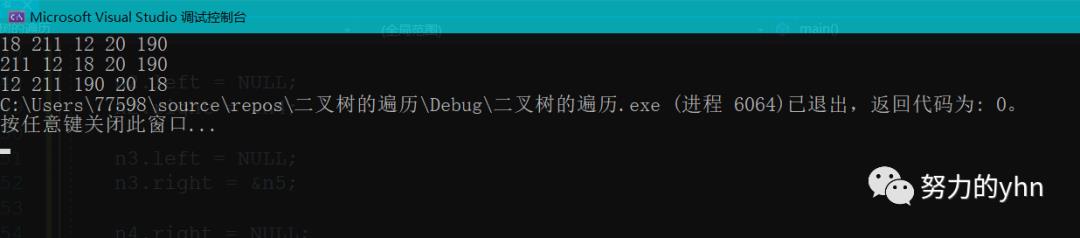
首先遍历根，然后分别遍历左子树和右子树。此过程将递归地应用于树的每个子树。根据此规则，上述二叉树的遍历结果为18, 211, 12, 20, 190

void preOrder(TreeNode *head_node) {
 if (head_node != NULL)
{
  printf("%d ", head_node->data);//打印根节点
  preOrder(head_node->left);//遍历左子树
  preOrder(head_node->right);//遍历右子树
}
}

中序遍历

首先遍历左侧子树，然后分别遍历根和右侧子树。此过程将递归地应用于树的每个子树。根据此规则，上述二叉树的遍历结果为211, 12, 18, 20, 190

void inOrder(TreeNode* head_node) {
 if (head_node != NULL)
{
  inOrder(head_node->left);//遍历左子树
  printf("%d ", head_node->data);//打印根节点
  inOrder(head_node->right);//遍历右子树
}
}

后序遍历

遍历左侧子树，然后分别遍历右侧子树和根。此过程将递归地应用于树的每个子树。根据此规则，上述二叉树的遍历结果为12, 211,190, 20, 18

    void postOrder(TreeNode* head_node) {
 if (head_node != NULL)
{
  postOrder(head_node->left);//遍历左子树
  postOrder(head_node->right);//遍历右子树
  printf("%d ", head_node->data);//打印根节点
}
}

全部测试代码

#include<stdio.h>
#include<stdlib.h>
typedef int ElemType;
typedef struct TreeNode {
 struct TreeNode* left, * right;
 ElemType data;
}TreeNode;

void preOrder(TreeNode *head_node) {
 if (head_node != NULL)
{
  printf("%d ", head_node->data);
  preOrder(head_node->left);
  preOrder(head_node->right);
}
}
void inOrder(TreeNode* head_node) {
 if (head_node != NULL)
{
  inOrder(head_node->left);
  printf("%d ", head_node->data);
  inOrder(head_node->right);
}
}

void postOrder(TreeNode* head_node) {
 if (head_node != NULL)
{
  postOrder(head_node->left);
  postOrder(head_node->right);
  printf("%d ", head_node->data);
}

}


int main() {
 TreeNode n1, n2, n3, n4, n5;
 n1.data = 18;
 n2.data = 211;
 n3.data = 20;
 n4.data = 12;
 n5.data = 190;

 n1.left = &n2;
 n1.right = &n3;

 n2.left = NULL;
 n2.right = &n4;

 n3.left = NULL;
 n3.right = &n5;

 n4.right = NULL;
 n4.left = NULL;

 n5.left = NULL;
 n5.right = NULL;

 preOrder(&n1);
 printf("
");
 inOrder(&n1);
 printf("
");
 postOrder(&n1);
 return 0;
}

输出结果

---

二叉搜索树

---

• 二叉搜索树可以定义为二叉树的一类，其中节点按特定的顺序排列。这也叫做有序二叉树。

• 在二叉搜索树中，左子树中所有节点的值都小于根节点的值。

• 类似地，右边子树中所有节点的值都大于或等于根的值。

• 此规则将递归地应用于根的所有左右子树。如下所示就是一个二叉搜索树。作为对BST（binary search tree）的约束，我们可以看到根节点30在其左子树中不包含任何大于或等于30的值，在其右子树中也不包含任何小于30的值。

二叉搜索树的优点

1. 在二叉搜索树中搜索变得非常有效，因为我们在每一步都得到了一个提示哪个子树包含所需的元素。

2. 相对于数组和链表，二叉搜索树被认为是一种高效的数据结构。在搜索过程中，每一步删除半个子树。在二叉搜索树中搜索一个元素需要o(log2n)时间。在最坏的情况下，搜索一个元素的时间是0(n)。

3. 与数组和链表中的插入和删除操作相比，它还加快了插入和删除操作的速度。

创建一个二叉树示例

43, 10, 79, 90, 12, 54, 11, 9, 50

43作为根节点，小于43的向左走，大于43的向右走，有空位即可插入，无空位继续向下探索，其整个过程如下所示：