每周算法平衡二叉树

Posted 2021-04-09 西南交通大学ACM协会

今天要给大家分享的平衡二叉树，建立在二叉排序树的基础上，目的是使二叉排序树的平均查找长度更小，即让各结点的深度尽可能小，因此，树中每个结点的两棵子树的深度不要偏差太大。

平衡因子的概念：结点的平衡因子 = 结点的左子树深度 — 结点的右子树深度。若平衡因子的取值为-1、0或1时，该节点是平衡的，否则是不平衡的。

 2.平衡化的实现

整个实现过程是通过在一棵平衡二叉树中依次插入元素(按照二叉排序树的方式)，若出现不平衡，则要根据新插入的结点与最低不平衡结点的位置关系进行相应的调整。分为LL型、RR型、LR型和RL型4种类型，各调整方法如下(下面用A表示最低不平衡结点)：

（1）LL型调整：

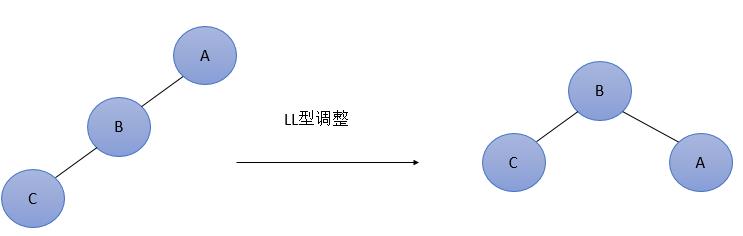
图1  最简单的LL型调整

由于在A的左孩子(L)的左子树(L)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由1增至2。图1是LL型的最简单形式。显然，按照大小关系，结点B应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，A结点就好像是绕结点B顺时针旋转一样。

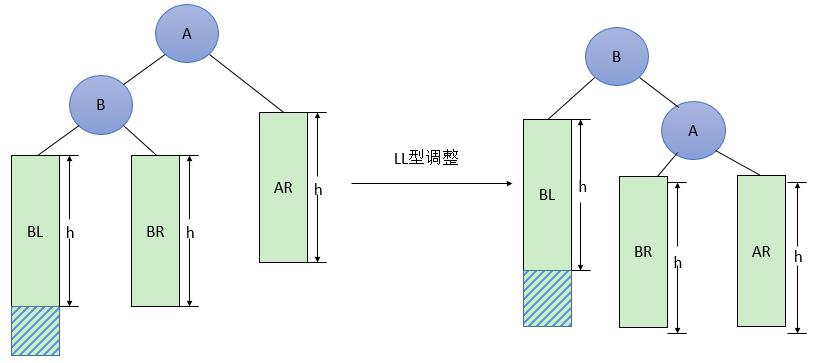
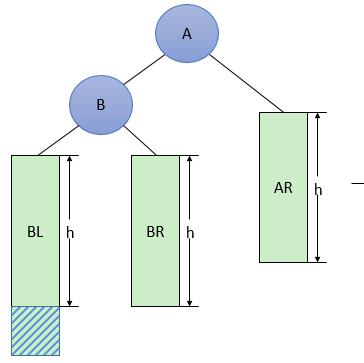
图2  一般形式的LL型调整

LL型调整的一般形式如图2所示，表示在A的左孩子B的左子树BL(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下：

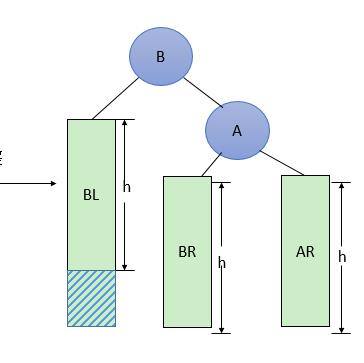
①将A的左孩子B提升为新的根结点；

②将原来的根结点A降为B的右孩子；

③各子树按大小关系连接(BL和AR不变，BR调整为A的左子树)。

（2）RR型调整：

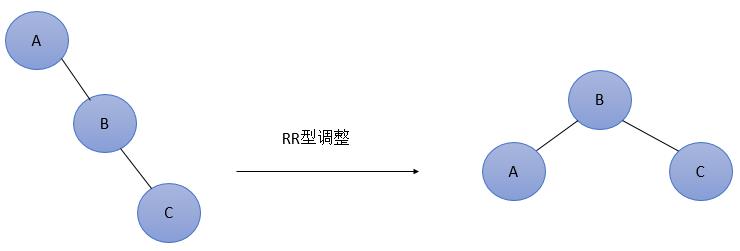
图3  最简单的RR型调整

由于在A的右孩子(R)的右子树(R)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由-1变为-2。图3是RR型的最简单形式。显然，按照大小关系，结点B应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，A结点就好像是绕结点B逆时针旋转一样。

2

1

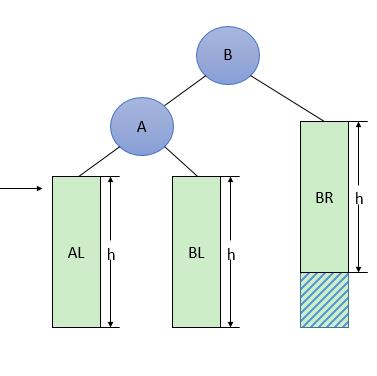
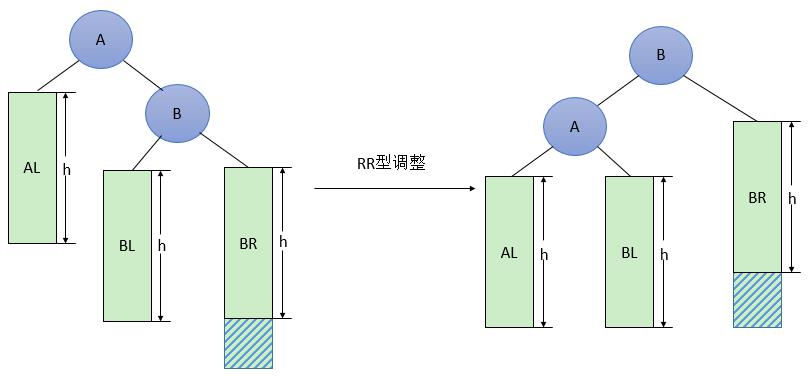
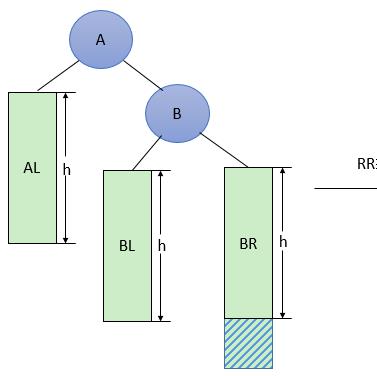
RR型调整的一般形式如下图4所示，表示在A的右孩子B的右子树BR(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下：

①将A的右孩子B提升为新的根结点；

②将原来的根结点A降为B的左孩子；

③各子树按大小关系连接(AL和BR不变，BL调整为A的右子树)。

（3）LR型调整：

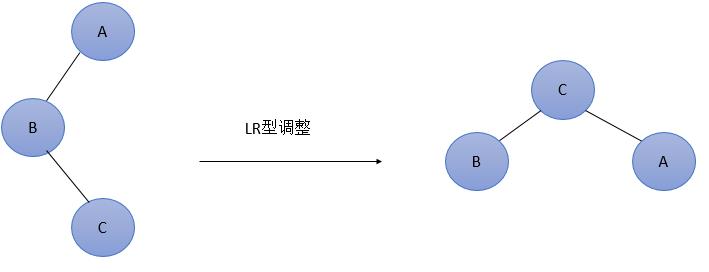
图5  最简单的LR型调整

由于在A的左孩子(L)的右子树(R)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由1变为2。图5是LR型的最简单形式。显然，按照大小关系，结点C应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡。

 1 

 2 

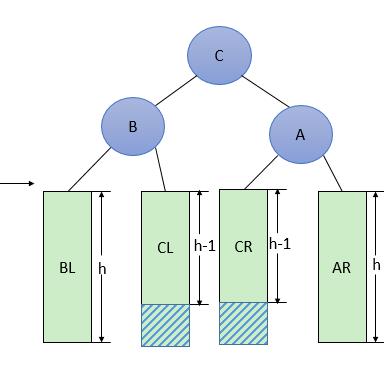
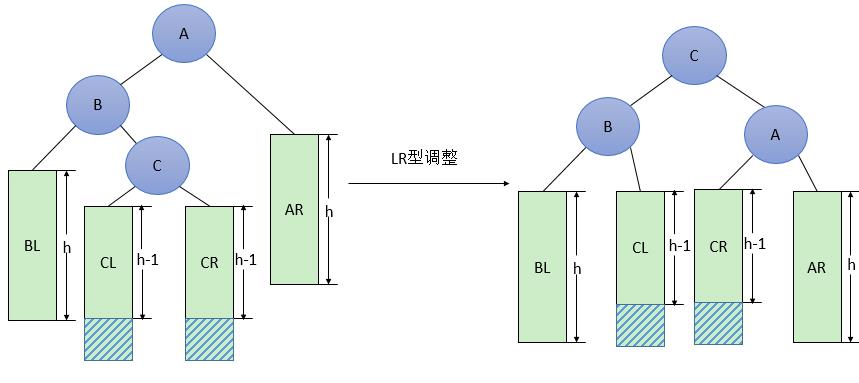
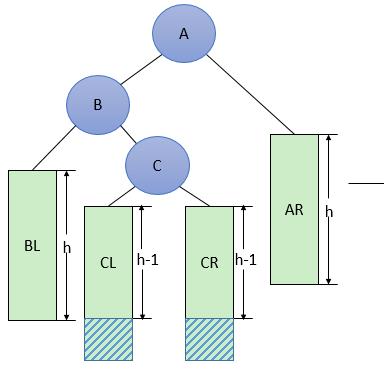
 3  一般形式的LR型调整

LR型调整的一般形式如下图6所示，表示在A的左孩子B的右子树(根结点为C，不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。这种情况调整如下：

①将C的右孩子B提升为新的根结点；

②将原来的根结点A降为C的右孩子；

③各子树按大小关系连接(BL和AR不变，CL和CR分别调整为B的右子树和A的左子树)。

（4）RL型调整：

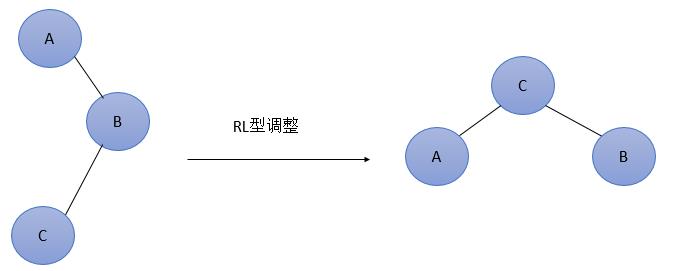
图7  最简单的RL型调整

——

由于在A的右孩子(R)的左子树(L)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由-1变为-2。图7是RL型的最简单形式。显然，按照大小关系，结点C应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡。

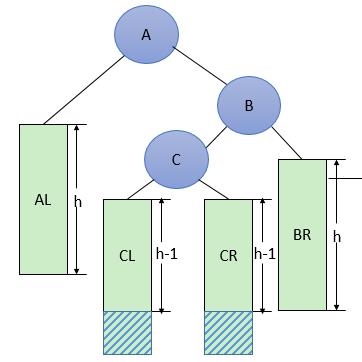
 1 

 2 

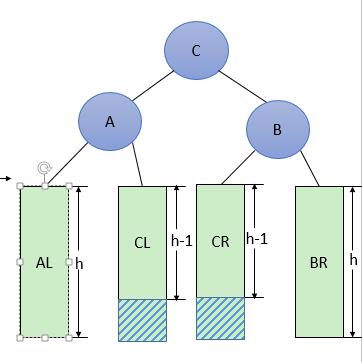
图8  一般形式的RL型调整

---------------

RL型调整的一般形式如图8所示，表示在A的右孩子B的左子树(根结点为C，不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。这种情况调整如下：

①将C的右孩子B提升为新的根结点；

②将原来的根结点A降为C的左孩子；

③各子树按大小关系连接(AL和BR不变，CL和CR分别调整为A的右子树和B的左子树)。

那么 今天就先分享到这里啦~

各位 下次见~

参考链接：

https://blog.csdn.net/qq_24336773/article/details/81712866