面试官让我手写一个平衡二叉树，我当时就笑了

Posted 2021-04-09 愚公要移山

平衡二叉树对于初学者一直是一个比较复杂的知识点，因为其里面涉及到了大量的旋转操作。把大量的同学都给转晕了。这篇文章最主要的特点就是通过动画的形式演示。确保大家都能看懂。最后是手写一个平衡二叉树。

一、概念

平衡二叉树是外国的两个大爷发明的。一开始发明的是二叉查找树。后来觉得不给力演化成了平衡二叉树。那什么是二叉查找树呢？我们给出一张图来看看：

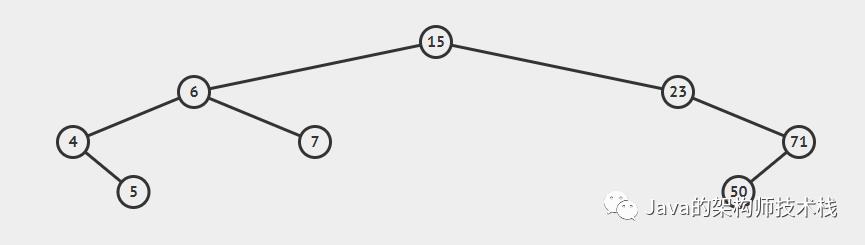
看到这张图我们就会发现如下的特征。从每个节点出发，左边的节点一定小于右边的。但是你会发现这可以高低不平，看起来很不美观。于是慢慢的演化成了平衡二叉树。（当然不是因为美观演化的）。也就是说平衡二叉树的前提就是一颗二叉查找树

平衡二叉树定义(AVL)：

（1）它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，

（2）它的左子树和右子树都是一颗平衡二叉树。

也就是说以上两条规则，只要破坏了一个就不是平衡二叉树了。比如说下面这张图。

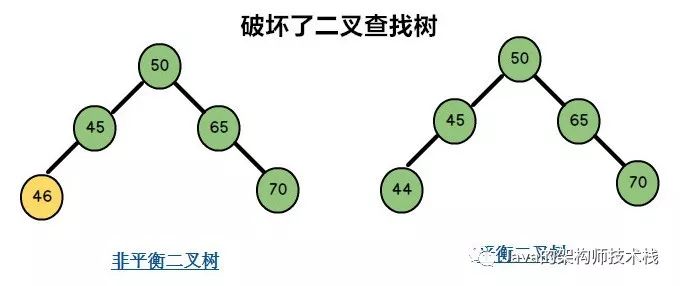
上面这张图就是破坏了二叉查找树这一条规则。当然了还有一条规则。也就是他的高度只差不能超过1.

现在相信我们已经明白了什么是平衡二叉树。下面我们就来看看平衡二叉树的增删改查操作是怎么样的。

二、平衡二叉树的插入操作

我们先从最简单的入手，一步一步来。

1、右旋

首先我们插入几个数字，50,45,44。通过动画我们来演示一遍

（1）插入50根节点不会出现任何操作

（2）插入45，往左边插入即可

（3）插入44，破坏了平衡，于是右旋。

2、左旋

我们插入几个数字，50,60,70。通过动画我们来演示一遍

（1）插入50根节点不会出现旋转

（2）插入60，往右边插入即可

（3）插入70，破坏了平衡，于是左旋。

3、先右旋再左旋

我们依次插入50,60,55.通过动画我们演示一遍

（1）插入55,根节点，不会出现旋转

（2）插入60，往右边插入

（3）插入55，破坏了平衡，于是先把55和60右旋，然后整体左旋。

4、先左旋后右旋

我们依次插入50,40,45.通过动画我们演示一遍。

（1）插入55,根节点，不会出现旋转

（2）插入40，往左边插入

（3）插入45，破坏了平衡，于是先把45和40左旋，然后整体右旋。

现在我们基本上已经把插入的几种情况罗列出来了。现在我们画一张图，来一个总结。

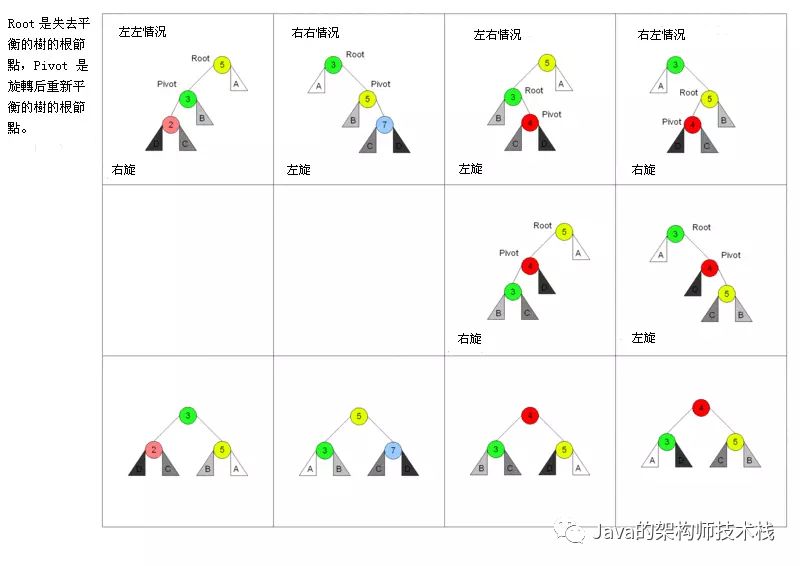
上图对于每一种情况，从上往下看就好了。对于平衡二叉树的删除操作，其实也是同样的道理，找到相应的元素之后，对其进行删除，删除之后如果破坏了平衡，只需要按照上面的这几种情况进行调整即可。下面我们来分析一下平衡二叉树的查找操作。

三、平衡二叉树的查找

平衡二叉树的查找很简单，只需要按照二叉查找树的顺序执行就好。我们使用一张动画演示一下：

现在平衡二叉树的操作相信你已经能够理解。下面我们就来关注最后一个问题，那就是如何手写一颗平衡二叉树呢？

四、手写一颗平衡二叉树

平衡二叉树的代码操作，难点在于旋转。只要把旋转弄清楚基本上整个树就能完成了，根据上面旋转的特点我们从零开始定义一颗。

第一步：定义节点

 1 public class AVLNode {
 2    public int data;//保存节点数据
 3    public int depth;//保存节点深度
 4    public int balance;//是否平衡
 5    public AVLNode parent;//指向父节点
 6    public AVLNode left;//指向左子树
 7    public AVLNode right;//指向右子树
 8
 9    public AVLNode(int data){
10        this.data = data;
11        depth = 1;
12        balance = 0;
13        left = null;
14        right = null;
15    }
16 }

第二步：插入数据

 1public void insert(AVLNode root, int data){
 2   //如果说插入的数据小于根节点，往左边递归插入
 3   if (data < root.data){
 4       if (root.left != null){
 5            insert(root.left, data);
 6       }else {
 7            root.left = new AVLNode(data);
 8            root.left.parent = root;
 9       }
10   }
11   //如果说插入的数据小于根节点，往左边递归插入
12   else {
13        if (root.right != null){
14            insert(root.right, data);
15        }else {
16            root.right = new AVLNode(data);
17            root.right.parent = root;
18       }
19  }
20  //插入之后，计算平衡银子
21   root.balance = calcBalance(root);
22  // 左子树高，应该右旋
23  if (root.balance >= 2){
24      // 右孙高，先左旋
25      if (root.left.balance == -1){
26          left_rotate(root.left);
27      }
28      right_rotate(root);
29  }
30  // 右子树高，左旋
31  if (root.balance <= -2){
32      // 左孙高，先右旋
33      if (root.right.balance == 1){
34          right_rotate(root.right);
35      }
36      left_rotate(root);
37  }
38  //调整之后，重新计算平衡因子和树的深度
39  root.balance = calcBalance(root);
40  root.depth = calcDepth(root);
41}

第三步：左旋和右旋的调整

1、右旋

 1    // 右旋
 2    private void right_rotate(AVLNode p){
 3        // 一次旋转涉及到的结点包括祖父，父亲，右儿子
 4        AVLNode pParent = p.parent;
 5        AVLNode pLeftSon = p.left;
 6        AVLNode pRightGrandSon = pLeftSon.right;
 7        // 左子变父
 8        pLeftSon.parent = pParent;
 9        if (pParent != null){
10            if (p == pParent.left){
11                pParent.left = pLeftSon;
12            }else if (p == pParent.right){
13                pParent.right = pLeftSon;
14            }
15        }
16        pLeftSon.right = p;
17        p.parent = pLeftSon;
18        // 右孙变左孙
19        p.left = pRightGrandSon;
20        if (pRightGrandSon != null){
21            pRightGrandSon.parent = p;
22        }
23        p.depth = calcDepth(p);
24        p.balance = calcBalance(p);
25        pLeftSon.depth = calcDepth(pLeftSon);
26        pLeftSon.balance = calcBalance(pLeftSon);
27    }

2、左旋

 1    private void left_rotate(AVLNode p){
 2        // 一次选择涉及到的结点包括祖父，父亲，左儿子
 3        AVLNode pParent = p.parent;
 4        AVLNode pRightSon = p.right;
 5        AVLNode pLeftGrandSon = pRightSon.left;
 6        // 右子变父
 7        pRightSon.parent = pParent;
 8        if (pParent != null){
 9            if (p == pParent.right){
10                pParent.right = pRightSon;
11            }else if (p == pParent.left){
12                pParent.left = pRightSon;
13            }
14        }
15        pRightSon.left = p;
16        p.parent = pRightSon;
17        // 左孙变右孙
18        p.right = pLeftGrandSon;
19        if (pLeftGrandSon != null){
20            pLeftGrandSon.parent = p;
21        }
22        p.depth = calcDepth(p);
23        p.balance = calcBalance(p);
24        pRightSon.depth = calcDepth(pRightSon);
25        pRightSon.balance = calcBalance(pRightSon);
26    }

第四步：计算平衡和深度

1、计算平衡

 1    public int calcBalance(AVLNode p){
 2        int left_depth;
 3        int right_depth;
 4        //左子树深度
 5        if (p.left != null){
 6            left_depth = p.left.depth;
 7        }else {
 8            left_depth = 0;
 9        }
10        //右子树深度
11        if (p.right != null){
12            right_depth = p.right.depth;
13        }else {
14            right_depth = 0;
15        }
16        return left_depth - right_depth;
17    }

2、计算深度

 1    public int calcDepth(AVLNode p){
 2        int depth = 0;
 3        if (p.left != null){
 4            depth = p.left.depth;
 5        }
 6        if (p.right != null && depth < p.right.depth){
 7            depth = p.right.depth;
 8        }
 9        depth++;
10        return depth;
11    }

看起来代码有些多，其实梳理一下就不多了。

（1）首先定义一个节点，里面有get和set方法，构造函数等等做准备工作

（2）直接写业务流程，比如说这里的insert操作，里面涉及到的旋转操作先用方法代替

（3）对主业务流程的操作，缺哪一个方法，写哪一个方法即可