二叉树知识点

Posted 2021-04-09 编程365

一、二叉树定义

二叉树是每个节点最多有两个子树的树结构，即二叉树中不存在度大于二的节点。并且，二叉树的子树有左右之分，其次序不能颠倒。

二、二叉树的性质

• 在二叉树的第i层上最多有2^(i-1)个结点

• 深度为k的二叉树最多有2^(i)-1个结点

• 对任意一个二叉树，若度为2的结点数为n2，叶子结点数为n0，则满足n0=n2+1

• 具有n个结点的完全二叉树的深度为 [log2 n]+1，[]表示下取整

三、三种遍历方式

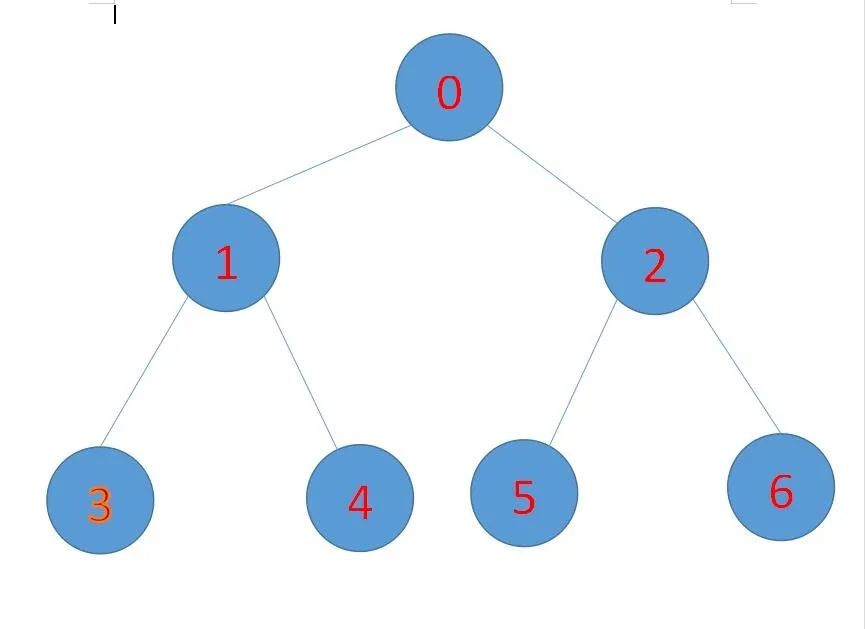
(1)先序遍历：先访问根节点，然后遍历左子树，最后遍历右子树；

在上图的二叉树中，结果为0 1 3 4 2 5 6

(2)中序遍历：先访问左子树，然后根节点，最后遍历右子树；

在上图的二叉树中，结果为3 1 4 0 5 2 6

(3)后序遍历：先遍历左子树，然后遍历右子树，最后访问根节点；

在上图的二叉树中，结果为 3 4 1 5 6 2 0

四、满二叉树和完全二叉树

1、满二叉树

一颗深度为k且有2^k-1个结点的二叉树称为满二叉树。

2、完全二叉树

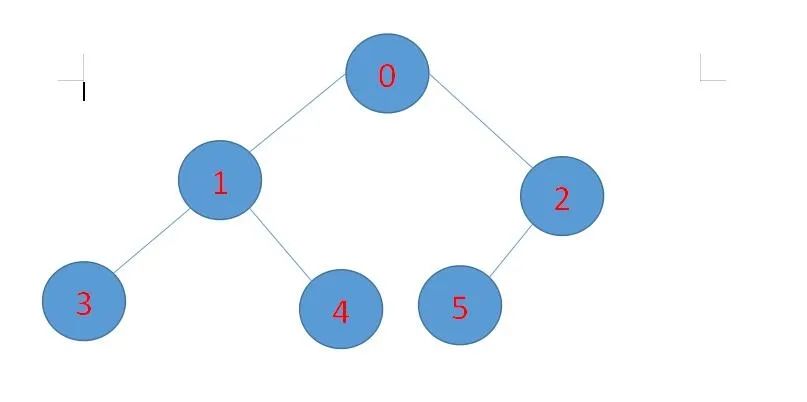
定义：深度为k的，有n个结点的二叉树，当且仅当每一个结点都与深度为k的满二叉树编号从1到n的结点一一对应时，称为完全二叉树。

特点：叶子节点只能出现在最后两层，且最下层的叶子节点集中在数的左部。

3、关系

显然，一颗满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

四、二叉查找树

1、定义：二叉查找树又被称为二叉搜索树。设x为二叉查找树中的一个结点，x结点包含关键字key，结点x的key值计为key[x]。如果y是x的左子树中的一个结点，则key[y]<=key[x]；如果y是x的右子树的一个结点，则key[y]>=key[x]。

2、性质

（1）若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。

（2）任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。

（3）任意结点的左、右子树也分别为二叉查找树。

（4）没有键值相等的结点。

---

---

扫码关注 编程365

我们一起用心编程

好看的人都点了在看