数据结构基础之平衡二叉树详解

Posted 2021-04-09 程序猿小哈

有趣有内涵的文章第一时间送达！

数据结构基础之平衡二叉树详解

前言

本文默认阅读人员已了解二叉树的相关概念,若不了解,可以点击二叉树查看二叉树的详解.

二叉搜索树

BST(Binary Search Tree)目的是为了提高查找的性能,使其查找在平均和最坏的情况下都是logn级别,接近二分查找.

其特点是：

1. 若它的左子树不空,则左子树上所有结点的值均小于它的根节点的值
2. 若它的右子树上所有结点的值均大于它的根节点的值
3. 它的左、右子树也分别为二叉搜索树

如图为二叉搜索树:

平衡二叉树

定义

平衡二叉树也称为AVL树,在二叉搜索树的基础上,平衡二叉树还需要满足如下条件:

• 左右两个子树的高度差( 平衡因子)的绝对值不超过1
• 左右两个子树都是一棵平衡二叉树

平衡因子（平衡度）:节点的左子树的高度减去右子树的高度(反之同理). 由此可知平衡二叉树是每个结点的平衡因子都为 1、－1、0 的二叉排序树,或者说每个结点的左右子树的高度最多差1的二叉排序树.所以平衡二叉树一定是二叉搜索树. 平衡二叉树的目的是为了减少二叉查找树层次,提高查找速度,常用实现方法有AVL、红黑树、替罪羊树、Treap、伸展树等.

Q:现在我们已经抓到了平衡二叉树的定义,那么来看看下图的两颗树拿个是平衡二叉树呢？

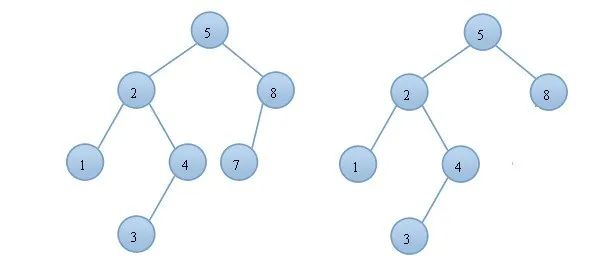
答案是左边,因为右边的树平衡因子是2.

这时候我想有的小伙伴就会问了,二叉搜索树在查找上就能用了,为什么还需要做一个平衡二叉树呢？平衡二叉树有什么好处吗？

为什么要使用平衡二叉树

我们知道，对于一般的二叉搜索树（Binary Search Tree）,其期望高度（即为一棵平衡树时）为log2n，其各操作的时间复杂度（O(log2n)）同时也由此而决定。但是，在某些极端的情况下（如在插入的序列是有序的时），二叉搜索树将退化成近似链或链，此时，其操作的时间复杂度将退化成线性的，即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况，但是在进行了多次的操作之后，由于在删除时，我们总是选择将待删除节点的后继代替它本身，这样就会造成总是右边的节点数目减少，以至于树向左偏沉。这同时也会造成树的平衡性受到破坏，提高它的操作的时间复杂度。例如：我们按顺序将一组数据1,2,3,4,5,6分别插入到一颗空二叉查找树和AVL树中，插入的结果如下图：

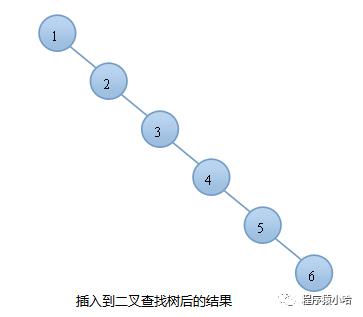
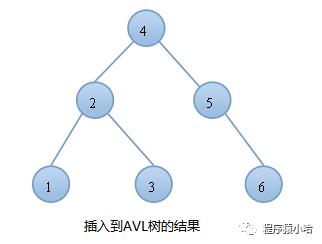
由上图可知，同样的结点，由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下，会导致二叉树的高度是O(N)，而AVL树就不会出现这种情况，树的高度始终是O(lgN).高度越小，对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因

这时候小伙伴又要提问了,那么AVL树这种结构要怎么样插入呢？这就是我们下面要说的自旋

自旋

树的自旋单旋转和双旋转. 我们先来说说单旋转的第一种情况--->右旋

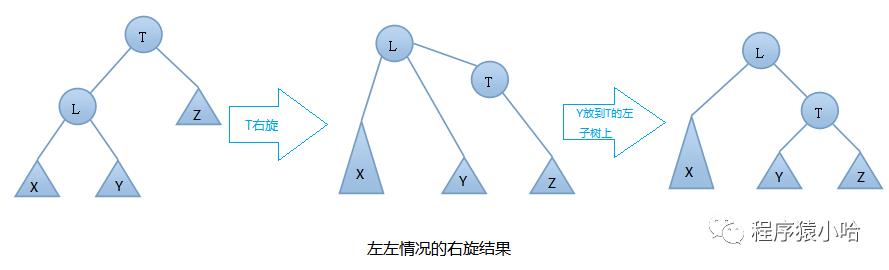
由上图可知：在插入之前树是一颗AVL树，而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏，我们要对其进行旋转。由上图可知我们是在结点T的左结点的左子树上做了插入元素的操作，我们称这种情况为左左情况，我们应该进行右旋转(只需旋转一次，故是单旋转)。具体旋转步骤是：

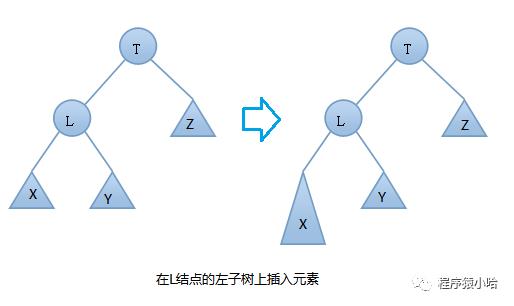
T向右旋转成为L的右结点，同时，Y放到T的左孩子上。这样即可得到一颗新的AVL树，旋转过程图如下：

相信聪明的小伙们看完右旋以后就可以举一反三知道左旋是如何达成了.那么看下下图然后思考一下左旋要怎么做

如果想不出来,可以私信左旋,或者联系作者获取答案哦.

接下来为什么再说说双自旋:

双旋转的第一种情况-->左右(先左后右)旋

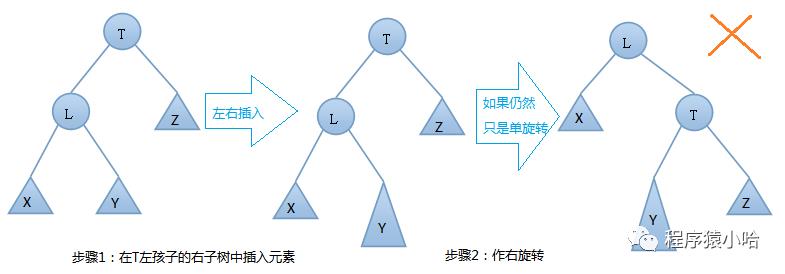
上图可知，我们在T结点的左结点的右子树上插入一个元素时，会使得根为T的树的左右子树高度差的绝对值不再 < 1,如果只是进行简单的右旋，得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转.

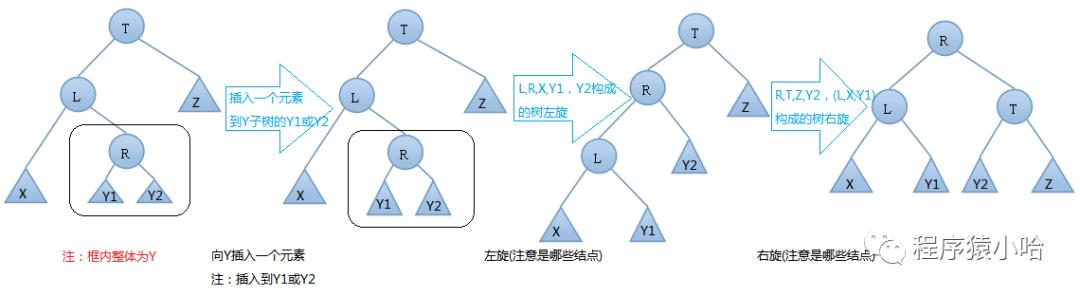
双旋转的第二种情况-->右左(先右后左)旋

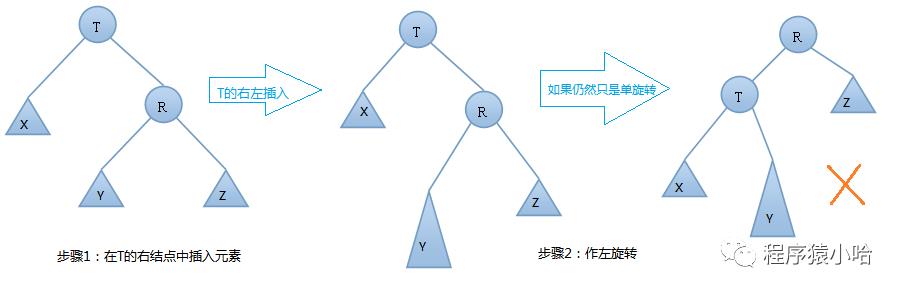
同样,聪明的小伙伴们可以思考一下,这样的情况下怎么旋转呢,如果想不出来,可以私信右左旋,或者联系作者获取答案哦.

可以联系作者获取C语言实现的平衡二叉树代码

总结

本文我们学习了平衡二叉树的一些基础知识,为后续学习红黑树打下了坚实的基础.明日为更新红黑树和八皇后问题详解,敬请期待.

猜你喜欢

关注订阅号程序猿小哈,联系作者,加入学习交流群和小伙伴们一起学习进步

你点的每个“在看”，我都认真当成了喜欢