牛逼!一文横扫二叉树的所有遍历方法
Posted 五分钟学算法
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了牛逼!一文横扫二叉树的所有遍历方法相关的知识,希望对你有一定的参考价值。
点击关注上方“五分钟学算法”,
设为“置顶或星标”,第一时间送达干货。
转自景禹
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
关于二叉树遍历的定义中有两个关键词:次序和访问。
二叉树的遍历次序不同于线性结构,线性结构最多也就是分为顺序、循环、双向等简单的遍历方式。
树的结点之间不存在唯一的前驱和后继这样的关系,在访问一个结点后,下一个被访问的结点面临着不同的选择。(这就像我们的人生路上一次次的抉择,考研还是工作!当然我们的选择不是像二叉树的选择,要么左,要么右,但我们既然选择了,一定要努力证明自己选择的正确性!)
单链表
若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。
我们可以简记为:中 → 左 → 右。我们先看一下动画演示,然后再来分析具体的实现方式:
class Solution {
ArrayList<Integer> list = new ArrayList<>();
//第一要素:明确你这个函数想要干什么
//函数功能:进行先序遍历二叉树
public List<Integer> preorderTraversal(TreeNode root) {
//第二要素:寻找递归结束条件
if(root == null)
return;
//第三要素:找出函数的等价关系式
list.add(root.val);//中
if(root.left != null)//左
preorderTraversal(root.left);
if(root.right != null)//右
preorderTraversal(root.right);
return list;
}
}
递归的执行过程中产生的递归树画起来不方便,而且存在大量冗余,景禹就不给大家演示了,而且在面试的时候,建议在给面试官给出递归的解法之后,能够再使用迭代进行解答。
上面的视频是二叉树的前序遍历的动画演示,你可以结合动画来看下面的迭代实现,需要注意的是,迭代实现中我们是先将根结点的右子节点入栈,然后在将左子节点入栈,这是因为栈的后进先出特性才如此处理的:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
LinkedList<TreeNode> stack = new LinkedList<>();
LinkedList<Integer> res = new LinkedList<>();
if (root == null) {
return res;
}
stack.add(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pollLast();
res.add(node.val);
if (node.right != null) {
stack.add(node.right);
}
if (node.left != null) {
stack.add(node.left);
}
}
return res;
}
}
02.
中序遍历
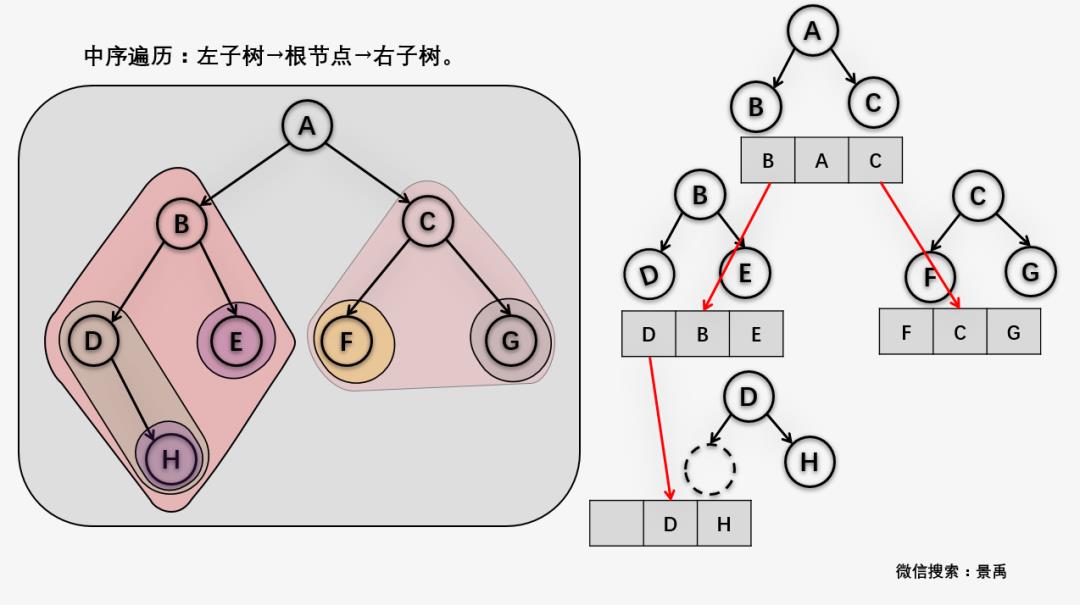
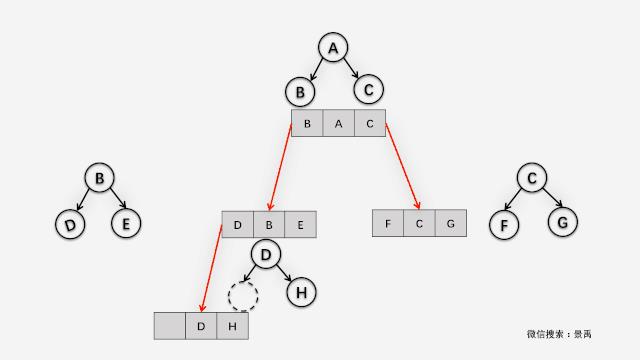
若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),先中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。
class Solution {
ArrayList<Integer> list = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
if(root == null)
return list;
if(root.left != null) //左
inorderTraversal(root.left);
list.add(root.val); //中
if(root.right != null) //右
inorderTraversal(root.right);
return list;
}
}
是不是觉着递归炒鸡简单呢?确实简单,不需要我们思考具体的执行过程,不过我们是学东西,再看一下迭代的实现。
public class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List <Integer> res = new ArrayList<>();
Stack <TreeNode> stack = new Stack<>();
TreeNode curr = root;
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.pop();
res.add(curr.val);
curr = curr.right;
}
return res;
}
}03.
后序遍历
若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点
我们可以简记为:左 → 右 → 中。先来看一下遍历的动画演示有一个直观的感受:
二叉树后序遍历的递归实现相当简单,只需要将前序遍历中res.add(root.val)移动到两个if语句之后即可。
class Solution {
ArrayList<Integer> list = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if(root == null)
return list;
if(root.left != null)//左
postorderTraversal(root.left);
if(root.right != null)//右
postorderTraversal(root.right);
list.add(root.val);中
return list;
}
}
我们着重分析一下后序遍历的迭代和取巧的实现方式,首先来看一下迭代的实现方式的动画演示(该视频包含迭代和取巧的两种方法的动画演示):
对照着上面的动画来看代码就轻松很多了,代码整体与中序遍历很相似,但需要注意其中两个点。第一,stack.peek()只是取出栈顶元素,要和stack.pop()弹出栈顶元素区分开来;第二,变量last用于保存当前栈顶所弹出的元素,判断 curr.right == last 是为了避免重复访问同一个元素而陷入死循环当中。
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
TreeNode last = null;
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.peek();
if (curr.right == null || curr.right == last) {
res.add(curr.val);
stack.pop();
last = curr;
curr = null;
} else {
curr = curr.right;
}
}
return res;
}
}class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<TreeNode> stack = new LinkedList<>();
LinkedList<Integer> res = new LinkedList<>();
if (root == null) {
return res;
}
stack.add(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pollLast();
res.addFirst(node.val);//每次在链表的头部插入元素
if (node.left != null) { //注意与前序对比着看
stack.add(node.left);
}
if (node.right != null) {
stack.add(node.right);
}
}
return res;
}
}层序遍历
若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
层序遍历是最简单的一种遍历方式,在考试和面试中很少涉及,但我们也不放过那5%的可能。万一遇到了呢?
由于每篇图文只能放三个视频,迫不得已我将后序遍历的两种方法的动画合并到了一个视频中,层序遍历就不给大家动画演示了,不过后续都是上传到景禹的视频号当中。
我们直接看一下代码,层序遍历中我们首先定义了一个保存遍历结果的数组res,然后定义了一个用于保存每一层结点的队列,队列满足先进先出的特性,我们在入队的时候一定是先左子节点,再右子节点(这样才符合从左到右的顺序对结点逐个访问),整个过程包裹在一个while循环之中,直到队列为空。
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
// 创建二维数组接收每层的结点
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
// 创建队列依次存放每层的结点
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
// 创建临时数组来存放每一层的结点
List<Integer> tmp = new ArrayList<>();
int len = q.size();
for (int i = 0; i < len; i++) {
// 定义 node 接收出队结点,然后加入数组 tmp 中
TreeNode node = q.poll();
tmp.add(node.val);
// 如果有左孩子,先将左孩子入队
if (node.left != null) {
q.add(node.left);
} //如果有右孩子,再将右孩子入队
if (node.right != null) {
q.add(node.right);
}
}
// 将tmp,也就是当前一层的节点对应的数组放入二维数组res中
res.add(tmp);
}
return res;
}
}
除了上面使用队列进行迭代的处理方法之外,我们依旧可以使用递归的方式进行解决,注意递归函数helper增加了一个记录当前处理节点的层数:
class Solution {
List<List<Integer>> res = new ArrayList<List<Integer>>();
public void helper(TreeNode node, int level) {
// 从当前的level层开始,创建一个当前层的数组并放入二维数组res中
if (res.size() == level)
res.add(new ArrayList<Integer>());
// 将当前层的节点添加到对应的level数组中
res.get(level).add(node.val);
// 处理下一层的孩子结点
if (node.left != null)
helper(node.left, level + 1);
if (node.right != null)
helper(node.right, level + 1);
}
public List<List<Integer>> levelOrder(TreeNode root) {
if (root == null) return res;
helper(root, 0);
return res;
}
}总结
二叉树的遍历包含四中遍历方法:前序遍历(中 → 左 → 右)、中序遍历(左 → 中 → 右)、后序遍历(左 → 右 → 中)和层序遍历。对于每一种遍历方式都可以使用递归的方式进行实现,其中前中后序还可以借助栈进行迭代实现,而层序遍历可以借助队列进行迭代实现。最后提醒大家,看完后记得去刷一下 LeetCode 【144. 94. 145. 102.】四道题目进行巩固一下!!!
推荐阅读:
以上是关于牛逼!一文横扫二叉树的所有遍历方法的主要内容,如果未能解决你的问题,请参考以下文章