树与二叉树

Posted 2021-04-09 前端应届生

1. 有一颗树的括号表示为A(B, C(E, F(G)), D)，回答下面的问题：

• 指出树的根结点？
• 指出棵树的所有叶子结点？
• 结点C的度是多少？
• 这棵树的度为多少？
• 这棵树的高度是多少？
• 结点C的孩子结点是哪？
• 结点C的双亲结点是谁？

答案：

这棵树的根结点为A
这棵树的叶子结点为B丶E丶G丶D // 叶子结点：一棵树当中没有子结点（即度为0）的结点称为叶子结点，简称“叶子”。叶子是指出度为0的结点，又称为终端结点。
结点C的度为2 // 结点度：结点拥有子结点的数量
这棵树的度是3 // 二叉树的度：是指树中各结点度的最大值
这棵树的高度为4 // 深度是从根节点到它的叶节点，高度是从叶节点数到它的根节点
节点C的孩子结点是E丶F
结点C的双亲结点是A 

2. 若一棵度为4的树中度为2丶3丶4的结点个数分别为3丶2丶2，则该树的叶子结点的个数是多少？

答案：

在树中，结点有几个分叉，度就是几。
树中结点数 = 总分叉树 + 1。（这里的分叉树就是所有结点的度之和）

❝

那么设叶子数为X，则此树的总分叉树为 2 * 3 + 3 * 2 + 4 * 2 = 20；树中结点数 = 总分叉树 + 1 = 20 + 1 = 21； 3 + 2 + 2 + X = 21，解得X = 14，即该树的叶子结点的个数为14。

❞

3. 为了实现以下各种功能，其中X结点表示该结点的位置，给出树的最适合的存储结构：

• 求X和Y结点的最近祖先结点
• 求X结点的所有子孙
• 求根结点到X结点的路径
• 求X结点的所有右边结点的路径
• 判断X结点是否是叶子结点
• 求X结点的所有孩子

答案：

双亲存储结构
孩子链存储结构
孩子兄弟存储结构
孩子存储结构
孩子链存储结构
孩子链存储结构  

4. 设二叉树BT的一种存储结构如表7.1所示。其中，BT为树根结点指针，Lichild丶rchild分别为结点的左丶右孩子指针域，在这里使用结点编号作为指针域值，0表示指针域值为空；data为结点的数据域。请完成下列问题：

• 画出二叉树BT的树形表示
• 写出按先序丶中序和后续遍历二叉树BT所得到的结点序列
• 画出二叉树BT的后续线索树（不带头结点）

答案：

• BT的逻辑结构

• 先序序列（根左右）： abcedfhgij
  中序序列（左根右）： acbhfdjiga   
  后序序列（左右根）： echfjigdba
  

• 先画出遍历序列，后根据遍历序列例如ABC，看A的右子树是否为空，如果为空，则指向B，再看B，如果B的左子树为空，则指向A，以此类推，均符合这个规律。

5. 含有60个叶子结点的二叉树的最小高度是多少？

答案

❝

叶子结点：一棵树中当中没有子结点（即度为0）的结点，称为叶子结点。叶子结点是指度为0的结点，又称为终端结点。

❞

❝

深度为h的二叉树最多有2^h - 1个节点

❞

❝

n0: 指度(分叉)为0的结点 n1：指度（分叉）为1的结点 n2：指度（分叉）为2的结点

❞

❝

二叉树中的叶子节点个数等于度为2的节点个数+1:  n0 = n2 + 1 证明链接

❞

答案：

在该二叉树中，n0 = 60，

n = n0 + n1 + n2 = n0 + n1 + (n0 -1) = 60 + n1 + (60 - 1) = 119 + n1;

当n1= 0且为完全二叉树时高度最小，

此时高度h = [log2^(n + 1)] = log(2)^120 = 7。所以含有60个叶子结点的二叉树最小高度是7

6. 已知一棵完全二叉树的第6层（设根结点为第1层）有8个叶子结点，则该完全二叉树的结点个数最多是多少？最少是多少？

❝

满二叉树和完全二叉树的区别：满二叉树：每层都达到最大数，称为满二叉树。完全二叉树：设二叉树的高度为h层，其他各层(1~h-1)的结点数都达到最大个数，第h层从右向左连续缺若干个结点。

❞

❝

满二叉树也是完全二叉树。

❞

答案：

完全二叉树的叶子结点只能在最下面两层，所以结点最多的情况是第6层为倒数第2层，即1~6层构成一棵满二叉树，其结点总数为2^6-1=63。
其中第6层有2^5=32个结点，含8个叶子结点，则另外有32-8=24个非叶子结点，它们中每个结点有两个孩子结点（均为第7层的叶子结点），计为48个叶子结点。
这样最多的结点个数 = 63 + 48 = 111。


结点最少的情况是第6层为最小层，即1~5层构成一棵满二叉树，其结点总数为2^5 - 1 = 31，再加上第6层的结点，总计31 + 8 = 39。
这样最少的结点个数为39。

7. 已知一棵满二叉树的结点个数为20~40之间，此二叉树的叶子结点有多少个？

答案：

满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

一棵高度为h的满二叉树的结点个数为2(h) -1，有20<=2(h)-1<=40。
则h=5，满二叉树中叶子结点均集中在最底层，
所以叶子结点个数=2*（5-1） = 16个

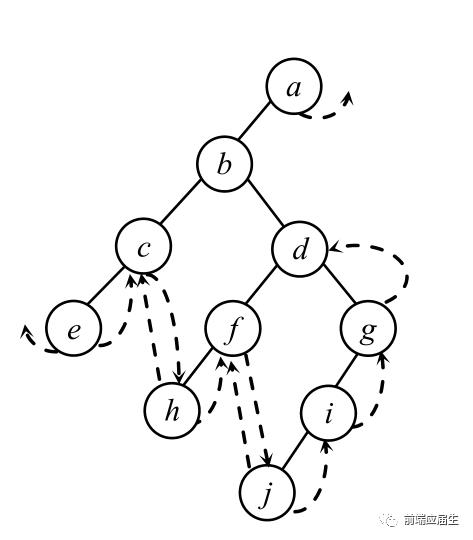
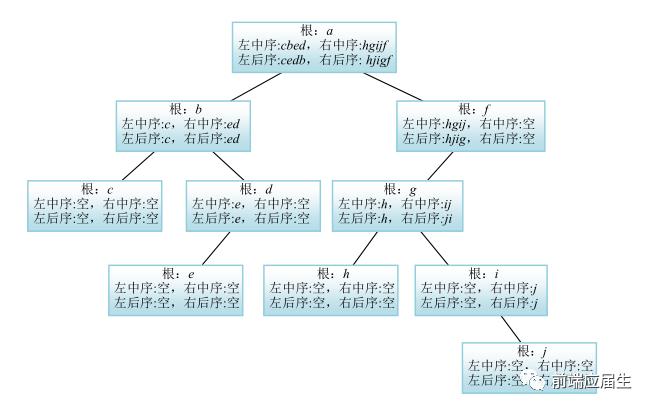
8. 已知一棵二叉树的中序序列为cbedahgijf，后序序列为cedbhjigfa，给出该二叉树树形表示。

答案：

9. 给定5个字符a~f，它们的权值集合W = {2, 3, 4, 7, 8, 9}，试构造关于W的一棵哈夫曼树，求其带权路径长度WPL和各个字符的哈夫曼树编码。

❝

哈尔曼树是带权路径长度最短的树，权值较大的结点离根较近。

❞

❝

哈夫曼树的构造方法：首先统计出每种字符出现的频率（也可以是概率）// 权值。第一步：找出字符中最小的两个，小的在左边，大的在右边，组成二叉树。在频率表中删除此次找到的两个数，并加入此次最小两个数的频率和。 点击了解详解

❞

❝

每个叶子到根的距离乘以叶子权值结果之和

❞

❝

添加0和1，规则左0 右1。

❞

❝

哈尔曼树和编码都不唯一的 只有WPL才是唯一的

❞

答案：

其带权路径长度WPL = (9 + 7 + 8) * 2 + 4 * 3 + (2 + 3) * 4 = 80。

各个字符的哈夫曼树编码：a: 0000  b: 00001 c: 001  d: 10 e: 11  f:01

10. 假设二叉树中每个结点的值为单个字符，设计一个算法将一棵以二叉链方式存储的二叉树b转换成对应的顺序存储结构a。

答案：

❝

顺序存储结构：该结构是把逻辑上的相邻的结点存储在物理位置上相邻的存储单元中，结点之间的逻辑关系由存储单元的邻接关系来体现。

❞

❝

void: 函数没有返回值 那么应声明为void类型。

❞

设二叉树的顺序存储结构类型为SqBTree，先将顺序存储结构a中所有元素置为'#'(表示空结点)。
将b转换成a的递归模型如下
f(b, a, i) = a[i] = '#;   当b = NULL
f(b, a, i) = 由b结点data域值建立a[i]元素；   其他情况
             f(b -> lchild, a, 2 * i);
             f(b -> rchild, a, 2 * i + 1);
 调用方式为：f(b, a, 1)(a的下标从1开始)。


 void Ctree(BTNode *b, SqBtree a, int) 
 {
     if(b != NULL) // 非空结点
     {
         a[i] = b -> data;
         Ctree(b -> lchild, a, 2 * i);
         Ctree(b -> rchild, a, 2 * i + 1);
     }     
     else // 空节点
     {
         a[i] = '#'; 
     }
 }

11. 假设二叉树中每个结点值为单个字符，采用顺序存储结构存储。设计一个算法，求二叉树t中的叶子结点个数。

答案：

用i遍历所有的结点，当i大于等于MaxSize，返回0。
当t[i]是空结点时返回0；
当t[i]是非空结点时，若它为叶子结点，num增1；
否则递归调用num1 = LeftNode(t, 2 * t)求出左子树的叶子结点个数num1，
再递归调用num2 = LeftNode(t, 2*i + 1)求出右子树的叶子结点个数num2，
置num += num1 + num2。最后返回num。


int LeftNode(SqBTree t, int i)
{
    int num1,
        num2,
        num = 0;
    if(i < MaxSize)
    {
        if(t[i] != '#') // 非空结点
        {
            if(t[2 * i] == '#' && t[2 * i + 1] == '#') // 叶子结点
            {
                num ++;
            }
            else 
            {
                num1 = LeftNode(t, 2 * i);
                num2 = LeftNode(t, 2 * i + 1);
                num += num1 + num2;
            }
            return num;
        }
        else 
        {
            retrun 0;
        }
    }    
    else 
    {
        return 0;
    }
}

12. 假设二叉树中每个结点值为单个字符，采用二叉树链存储结构存储。设计一个算法计算给定二叉树b中的所有单分支结点个数。

答案：

计算一棵二叉树的所有单分支结点个数的递归模型f(b)如下：
f(b) = 0   若b = NULL;
f(b) = f(b -> lchild) + f(b -> rchild) + 1;  若b结点为单分支
f(b) = f(b -> lchild) + f(b -> rchild)  其他情况


int SSonNodes(BTNode *b)
{
    int num1, 
        num2 , 
        n;
    if(b == NULL) // 空结点
    {
        return 0;
    }    
    else if((b -> lchild == NULL && b -> rchild != NULL) || (b -> lchild != NULL && b -> rchild == NULL)) // 为单个分支结点
    {
      n = 1;
    }
    else 
    {
      n = 0;
    }

    // 递归
    num1 = SSonNodes(b -> lchild); // 递归求左子树单分支结点数
    num2 = SSonNodes(b -> rchild);  // 递归求右子树单分支结点数
    return (num1 + num2 + n);
}

13. 假设二叉树中每个结点值为单个字符，采用二叉树存储结构存储。设计一个算法求二叉树b中最小值的结点值。

答案：

设f(b, min)是在二叉树b中寻找最小结点值min，其递归模型如下
f(b, min) = 不做任何事件  // 若b = NULL
f(b, min) = 当b -> data < min时置min = b -> data; // 其他情况
            f(b -> lchild, min);f(b -> rchild, min);
 

 void FindMinNode(BTNode *b, char min)// void的作用：1.当函数不需要返回值时，必须使用void限定  2. 当函数不允许接受参数时，必须使用void限定
 {
     if(b -> data < min) // 当前结点值比最小值小则置换
     {
         min = b -> data;
     }
     // 递归
     FindMinNode(b -> lchild, min); // 在左子树中找最小结点值
     FindMinNode(b -> rchild, min); // 在右子树中找最小结点值
 }
 void MinNode(BTNode *b) // 输出最小结点值
 {
     if(b != NULL) // 非空结点
     {
         char min = b -> data; // char是容纳单字符的一种基本数据类型
         FindMinNode(b, min);
         printf("Min = %c
", min);
     }
 }

14. 假设二叉树每个结点值为单个字符，采用二叉树存储结构存储。设计一个算法将二叉树b1复制到二叉链b2中。

答案：

当b1为空时，置b2为空树。
当b1不为空时，建立b2结点（b2为根结点），置b2 -> data = b1 -> data；
递归调用Copy(b1 -> lchild, b2 -> lchild)，由b1的左子树建立b2的左子树；
递归调用Copy(b1 -> rchild, b2 -> rchild)，由b1的右子树建立b2的右子树。
对应的算法如下：


void Copy(BTNode *b1, BTNode *&b2)
{
    if(b1 == NULL)
    {
        b2 = NULL;
    }
    else 
    {
        b2 = (BTNode *)malloc(sizeof(BTNode)); // malloc：动态分配   BTNode *：强制转换为   sizeof(BTNode)：为了获取BTNode类型占据空间的大小
        b2 -> data = b1 -> data;

        // 递归   
        Copy(b1 -> lchild, b -> lchild);
        Copy(b1 -> rchild, b -> rhcild);
    }
}

15. 假设二叉树中每个结点值为单个字符，采用二叉链存储结构存储。设计一个算法，求二叉树b中第K层上叶子结点个数。

答案：

采用先序遍历方法，当B为空时返回0。置num为0。
若b不为空，当前结点的层次为K，并且b为叶子结点，则num增1，递归，
递归调用num1 = LevelkCount(b -> child, k, h+1)求出左子树中第K层的结点个数num1，
递归调用num2=LevelKCount(b -> rchild, k, h + 1)求出右子树中第K层的结点个数num2，
置num += num1 + num2，最后返回num。
对应的算法如下


int LevelkCount(BTNode *b, int k, int h)
{
    int num1, 
        num2, 
        num = 0;
    if(b != NULL) // 非空结点
    {
        if(h == k && b -> lchild == NULL && b -> rchild == NULL) // 叶子结点
        {
            num ++;
        }

        // 递归   
        num1 = LevelkCount(b -> lchild, k, h + 1);
        num = LevelkCOunt(b -> rchild, k, h + 1);
        num += num1 + num2;
        return num;
    }
    return 0;
}
int Levelkleft(BTNode *b, int k)
{
    return  LevelkCount(b, k, 1);
}

16. 假设二叉树中每个结点值为单个字符，采用二叉树结构存储。设计一个算法，判断值为X的结点与值为Y的结点是否互为兄弟，假设这样的结点值是唯一的。

答案：

采用先序遍历，当b为空时直接返回false，
否则，若当前结点b是双分支结点，且有互为兄弟的结点x丶y，则返回true；
否则，递归调用flag=Brother(b->lchild, x, y)，求出x丶y在左子树是否互为兄弟，若flag为true，则返回true；
否则递归调用Brother(b->rchild, x, y)，求出x丶y在右子树中是否互为兄弟，并返回其结果。
对应的算法如下：
 

 bool Brother(BTNode *b, char x, char y)
 {
     bool flag;
     if(b == NULL)
     {
         return false;
     }
     else 
     {
         if(b -> lchild != NULL && b -> rchild != NULL) // 左兄弟结点和
         {
             if((b -> lchild -> data === x && b -> rchild -> data == y))
             {
                 return true;
             }

             // 递归
             flag = Brother(b -> lchild, x, y);
             if(flag == true)
             {
                 return true;
             }
             else 
             {
                 return Brother(b -> rchild, x, y);
             }
         }
     }
 }

17.假设二叉树中每个结点值为单个字符，采用二叉链存储结构存储。设计一个算法，采用先序遍历方法求二叉树b中值为x的结点的子孙，假设值为x的结点是唯一的。

答案：

设计Output(p)算法输出以p为根结点的所有结点。
首先在二叉树b中查找值为X的结点，当前b结点是这样的结点，调用Output(b->lchild)输出其左子树中所有结点，调用Output(b->rchild)输出其右子树中所有结点，并返回；
否则，递归调用Child(b->lchild, x)在左子树中查找值为X的结点，递归调用Child(b->rchild, x)在右子树中查找值为X的结点。对应的算法如下 
 

 void Output(BTNode *p) 
 {
     if(p != NULL)
     {
         printf("%c", p -> data);
         Output(p -> lchild);
         Output(p -> rchild);
     }
 }
 viod Child(BTNode *b, char x)
 {
     if(b != NULL)
     {
         // 找到为X的结点
         if(b -> data == x)
         {
             if(b -> lchild != NULL)
             {
                 Output(b -> lchild);
             }
             if(b -> rchild != NULL)
             {
                 Output(b -> rchild);
             }
             return;
         }

         // 找不到为X的结点 则继续递归
         Child(b -> lchild, x);
         Child(b -> rchild, x);
     }
 }

18.假设二叉树采用二叉树存储，设计一个算法把二叉树b的左丶右子树进行交换。要求不破坏原二叉树。并用相关数据进行测试。

答案：

交换二叉树的左丶右子树递归模型如下：
 f(b, t) = t = NULL  若b = NULL
 f(b, t) = 复制根结点b产生结点t； 其他情况
           f(b -> lchild, t1); f(b -> rchild, t2);
           t -> lchild = t2;  t ->  rchild = t1
 对应的算法如下（算法返回左丶右子树交换后的二叉树）
 

 #include "btree.cpp" // 二叉树基本运算算法
 BTNode *Swap(BTNode *b)
 {
     BTNode *t,
            *t1,
            *t2;
     if(b == NULL)
     {
         t = NULL;
     }       
     else
     {
         t = (BTNode *)malloc(sizeof(BTNode));
         t -> data = b -> data; // 复制产生根结点t
         t1 = Swap(b -> lchild);
         t2 = Swap(b -> rchild);
         t -> lchild = t2;
         t -> rchild = t1;
     }
     return t;
 }
 // 或者设计成如下算法（算法产生左丶右子树交换后的二叉树b1）
 vold Swap1(BTNode *b, BTNode *&b1)
 {
     if(b == NULL)
     {
         b1 = NULL;
     }
     else 
     {
         b1 = (BTNode *)malloc(sizeof(BTNode));
         b1 -> data = b -> data;
         Swap1(b -> lchild, b1 -> rchild);
         Swap1(b -> rchild, b1 -> lchild);
     }
 }

 // 设计如下主函数
 int main()
 {
     BTNode *b,
            *b1;
     CreateBTree(b, "A(B(D(G)), C(E, F))");
     printf("交换前的二叉树：");DispBTree(b);printf("
");
     b1 = Swap(b);
     printf("交换后的二叉树：");DispBTree(b1);printf("
");
     DestroyBTree(b);
     DestroyBTree(b1);
     return 1;        
 }
 程序执行结果如下：
 交换前的二叉树：A(B(D(,G)), C(E, F));
 交换后的二叉树：A(C(F, E), B(, D, (G)))

19.假设二叉树采用二叉链式存储结构，设计一个算法判断一棵二叉树b的左丶右子树是否同构。

答案：

❝

给定两颗二叉树T1和T2，如果T1可以通过若干次左右孩子互换变成T2，则我们称为两颗二叉树是同构的。

❞

 判断二叉树b1丶b2是否同构的递归模型如下： 
 f(b1, b2) = true  b1= b2 = NULL
 f(b1, b2) = false  若b1丶b2中有一个为空，另一个不为空
 f(b1, b2) = f(b1 -> lchild, b2 -> lchild) & f(b1 -> rchild, b2 -> rchild)    
 对应的算法如下
   
 bool Symm(BTNode *b1, BTNode * b2) // 判断二叉树b1和b2是否同构
 {
     if(b1 == NULL && b2 == NULL)
     {
         return true;
     }
     else if(b1 == NULL || b2 == NULL)
     {
         return false;
     }
     else {
         return (Symm(b1 -> lchild, b2 -> lchild) & Symm(b1 -> rchild, b2 -> rchild));
     }
 }
 bool Symmtree(BTNode *b) // 判断二叉树的左丶右子树是否同构
 {
     if(b == NULL)
     {
         return true;
     }
     else {
         retrun Symm(b -> lchild, b -> rchild);
     }
 }

20.假设二叉树以二叉树存储，设计一个算法，判断一棵二叉树B是否为完全二叉树。

答案：

根据完全二叉树的定义，对完全二叉树按照从上到下丶从左到右的次序遍历（层次遍历）应该满足：
某结点没有左孩子，则一定无右孩子
若某结点缺左或右孩子（一旦出现这种情况，置bj = false），则其所有后继一定无孩子。
若不满足上述如何一种，均不为完全二叉树（cm = true表示是完全二叉树，cm = false表示不是完全二叉树）。
对应的算法如下：
    
  bool CompBtree(BTNode *b)
  {
      BTNode *Qu(MaxSize), // 定义一个队列，用于层次遍历 
              *p; 
      int front = 0, // 环形队列的对头指针
          rear = 0;  // 环形队列的队尾指针 
      bool cm = true; // cm为真表示二叉树完全二叉树
      bool bj = true; // bj为真表示到目前为止所有结点均有左右孩子
      if(b = NULL) // 空树当成特殊的完全二叉树
      {
          return true;
      }           
      rear ++;
      Qu[rear] = b; // 根结点进队
      while(front != rear) // 队列不空
      {
          front = (fornt + 1) % MaxSize;
          p = Qu[front]; // 出队结点p
          if(p -> lchild == NULL) // p结点没有左孩子
          { 
              bj = false; // 出现结点P缺失左孩子的情况
              if(p -> rchild != NULL) // 没有左孩子但有右孩子，违反（1）
              {
                  cm = false;
              }
          }
          else // p结点有左孩子
          {
              if(!bj) // bj为假而结点p还有左孩子，违反（2）
              {
                  cm = false;
              }
              rear = (rear + 1) % MaxSize;
              Qu[rear] = p -> lchild; // 左孩子进队
              if(p -> rchild == NULL)
              {
                  bj = false; // 出现结点P缺失右孩子的情况
              }
              else 
              {
                  rear = (rear + 1) % MaXSize;
                  Qu[rear] = p -> rchild; // 将p结点的右孩子进队
              }
          }
      }
      return cm;
  }

如果你看完觉得这篇文章不错，帮我两件小事

• 加我备注 【加群】 拉你进超级前端交流群，和各大厂的同学一起交流学习，共同进步。