强！深度优先遍历求二叉树的直径

Posted 2021-04-09 算法的秘密

今天这道题，本质上也是二叉树的深度优先遍历。建议你配合本专辑其他文章一起食用，风味更佳。

1 问题描述

给定一个二叉树，请计算它的直径。所谓直径，就是路径距离最长的两个叶子节点的路径上的节点个数。

例子1

如下二叉树：

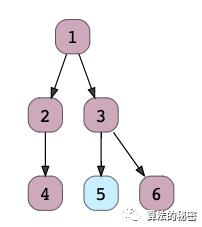
输出：5

代表直径的路径是  [4, 2, 1, 3, 6]

例子2

如下二叉树：

输出：7

代表直径的路径是  [10, 8, 5, 3, 6, 9, 11]

2 问题分析

复杂的问题往往可以用简单的思维解决。

这个问题仍然可以从暴力搜索的角度来解决。找到所有两两叶子节点之间的路径，比较这些路径，找出最长的即可。

问题是，如何穷尽所有路径？

观察上面的两个图可以发现，我们可以将所有路径，按照它们的顶点所在节点进行分类。

以某个节点为顶点的所有路径中，我们也不用逐个路径去检查。因为只有最长的路径是我们需要的，所以我们可以找出该节点左右子树的高度，再加上1（代表该节点）就是以该节点为顶点的所有路径中最长的那个。

如果你看了，会发现，这两个问题看似不相同，但是思维方式却是完全一样。都是从暴力求解的思维出发，然后将所有候选结果按照树的节点进行分类，再用深度优先遍历每一个节点，逐步算出结果。

3 代码实现

class TreeNode:
  def __init__(self, val, left=None, right=None):
    self.val = val
    self.left = left
    self.right = right


class TreeDiameter:

  def __init__(self):
    self.treeDiameter = 0

  def find_diameter(self, root):
    self.calculate_height(root)
    return self.treeDiameter

  def calculate_height(self, currentNode):
    if currentNode is None:
      return 0

    leftTreeHeight = self.calculate_height(currentNode.left)
    rightTreeHeight = self.calculate_height(currentNode.right)

    # 以当前节点为顶点的路径中，最长的就是
    # 左右子树的高度加1
    diameter = leftTreeHeight + rightTreeHeight + 1

    # 更新全局最长的直径
    self.treeDiameter = max(self.treeDiameter, diameter)

    # 计算以当前节点为根的子树的高度
    return max(leftTreeHeight, rightTreeHeight) + 1

推荐阅读：