二叉树入门学习

Posted 2021-04-09 2019在这里

二叉树入门学习

最近数据结构课学习到了二叉树，就给大家介绍两种二叉树吧！

二叉排序树二叉排序树具有以下性质

若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
它的左右子树也分别为二叉排序树。

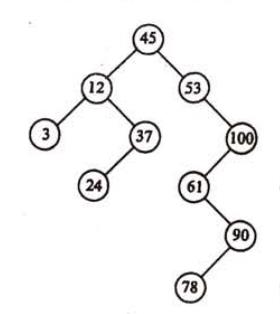
就像这张图里面画的，根节点45的左边所有节点的值都是小于45的，右边所有节点的值都是大于45的，把其他节点看作根节点也是一样的。

那么我们如何建立一个这样的二叉树呢？下面上代码。

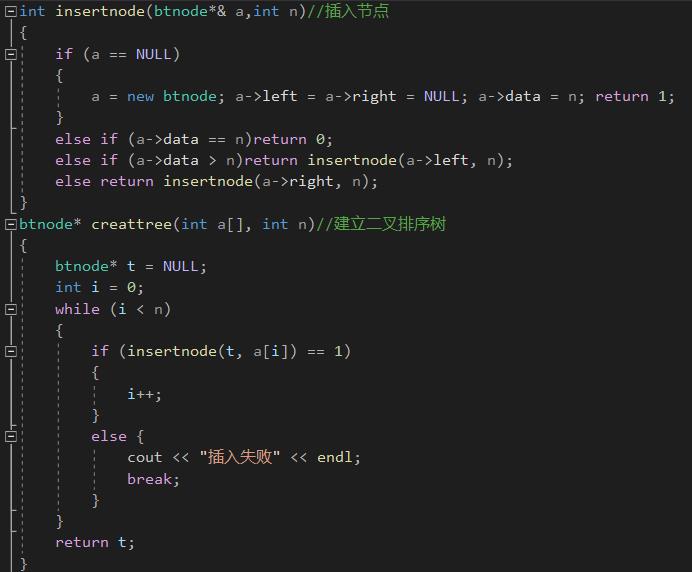
假如我们把数据都存储到一个数组里面，然后遍历这个数组来获取数据。

数组的第一个数据就是二叉排序树的根节点，其余数据与二叉树里面的数据一个个比较直到遇到叶子节点，然后如果这个数据比叶子节点大则加入到它的右边，小则左边。

优点:这样一种树的结构方便我们对数据进行查找，但是也有局限性，举个例子。

假如我们的数据是这样的：int a[5]={1,2,3,4,5};

那么二叉排序树就是这样的：

这样的二叉排序树是没有意义的。(实际上它变成了一条链表)

 

我们可以用平衡二叉树来解决这样的问题。

平衡二叉树（Balanced Binary Tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

 

如果使用二叉平衡树，上图就会变成：

不同的算法会有不同的结果，但是它们都会保持左右子树高度差不超过1；

由于代码比较长也比较复杂，这里就不展示了，感兴趣的同学可以去查找资料。

- END -

                                                       图 | 李子健

                                                       文 | 李子健

                                              排版 | 夏晶 李子健

                                                       审核 | 夏晶

                                 关键词回复

                     课表 | 校历 | 早自习 | 晚自习

              脱单 | 宿舍报修 | 在读证明 | 宿舍服务