二叉树之前序中序后序和层次遍历图文教程

Posted 2021-04-09 IT特靠谱

平凡也就两个字: 懒和惰;
成功也就两个字: 苦和勤;
优秀也就两个字: 你和我。
跟着我从0学习JAVA、spring全家桶和linux运维等知识，带你从懵懂少年走向人生巅峰，迎娶白富美！
每一篇文章都是心得总结，跟我学习你就是大牛！

二叉树之前序、中序、后序和层次遍历【图文教程】

1 简介

      二叉树（binary tree）是指树中节点长度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树——百度百科。

     在java中有很多数据结构是基于二叉树的，比如TreeSet和TreeMap是二叉树结构，HashMap的红黑树结构是一种自平衡的二叉树结构。下面将讲述二叉树遍历的三种方式：前序遍历、中序遍历和后序遍历。

2 四种遍历方式

      首先我们有如下一颗二叉树：

（1）前序遍历：根结点 —> 左子树 —> 右子树（先遍历根节点，然后左右）。这棵树的前序遍历为：ABDEGHCF

（2）中序遍历：左子树—> 根结点 —> 右子树（在中间遍历根节点）。这棵树的中序遍历为：DBGEHACF

（3）后序遍历：左子树 —> 右子树 —> 根结点（最后遍历根节点）。这棵树的后序遍历为：DGHEBFCA

（4）层次遍历：按层次遍历。这棵树的层次遍历为：ABCDEFGH

      总结： 所谓的前序、中序、后续，就是对根节点而言的，左右的遍历顺序不变，前序就是根节点最先遍历，然后左右；中序就是把根节点放在中间遍历；后序则是把根节点放在最后遍历。反过来，我们知道了遍历方式和遍历顺序后，我们就可以推算出二叉树的结构！

3 推算二叉树结构

    需求：已知二叉树前序遍历为：ABDEGHCF，中序遍历为：DBGEHACF，求二叉树结构?

    分析：首先我们由前序遍历可知根节点为A。已知根节点为A，由中序遍历可知左子树为DBGEH,右子树为CF。确定这两点后就很容易推算出原来的二叉树的样子了。我们看到右子树节点为CF，中序遍历也是CF，那么就可以推断出现在的二叉树右边是这个样子：

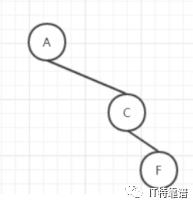
      为什么F不是左子树呢，因为如果F在左边，中序遍历的顺序就变成FC了。由前序遍历AB可以知，A的左子树肯定是B，那么现在的树就是这样的：

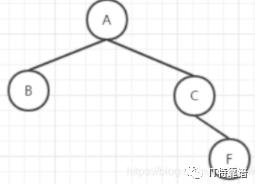
      再由中序遍历DB可知，D为B的左子树。

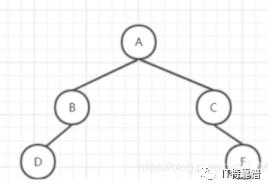
      现在只剩下EGH没确定了。首先我们要确定的是D肯定没有子树，如果有，中序遍历就不会是DB了。由前序遍历可知E节点只能是B的右子树了

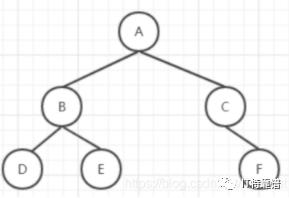
      最后由中序遍历GEH可知完整的二叉树为：

       如果以上教程对您有帮助，为了不迷路或需要技术支持，请关注一下吧~