数据结构之树(二叉树)的探索
Posted 码农迪迪
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构之树(二叉树)的探索相关的知识,希望对你有一定的参考价值。
点击蓝字
默默关注
树的定义:
树(Tree)是n(n≥0)个结点的有限集,它或为空树(n = 0);或为非空树,对于非空树T:
(1)有且仅有一个称之为根的结点;
(2)除根结点以外的其余结点可分为m(m>0)个互不相交的有限集T1, T2, …, Tm, 其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)
图示:
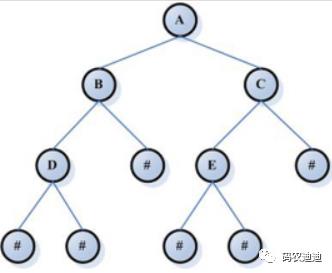
基本术语表
根 |
即根结点(没有前驱) |
叶子 |
即终端结点(没有后继) |
森林 |
m颗不相交的树集合 |
有序树 |
结点各子树从左至右有序,不能互换 |
无序树 |
结点各子树可互换位置 |
双亲 |
即上层的那个结点(直接前驱) |
孩子 |
即下层结点的子树的根(直接后继) |
兄弟 |
同一双亲下的同层结点(孩子之间互称兄弟) |
堂兄弟 |
即双亲位于同一层的结点(但并非同一双亲) |
祖先 |
即从根到该结点所经分支的所有结点 |
子孙 |
即该结点下层子树中的任一结点 |
结点 |
即树的数据元素 |
结点的度 |
结点挂接的子树数 |
结点的层次 |
从根到该结点的层数(根结点算第一层) |
终端结点 |
即度为0的结点,即叶子 |
分支节点 |
即度不为0的结点(也称为内部结点) |
树的度 |
所有结点度中的最大值 |
树的深度(高度) |
指所有结点中最大的层数 |
二叉树(Binary Tree)是n(n≥0)个结点所构成的集合,它或为空树(n = 0);或为非空树,对于非空树T:
(1)有且仅有一个称之为根的结点;
(2)除根结点以外的其余结点分为两个互不相交的子集T1和T2,分别称为T的左子树和右子树,且T1和T2本身又都是二叉树。
二叉树基本特点:
•结点的度小于等于2
•有序树(子树有序,不能颠倒)
二叉树的性质:
性质1: 在二叉树的第i层上至多有2^(i-1)个结点
性质2: 深度为k的二叉树至多有2^k-1个结点
性质3: 对于任何一棵二叉树,若2度的结点数有n2个,则叶子数n0必定为n2+1(即n0=n2+1)
证:边的个数B等于结点数n-1(树的性质),也会等于度为2的点n2乘以2加上度为一的点n1乘以1,即B=n-1且 B=n2*2+n1*1 且 n=n2+n1+n0即可证。
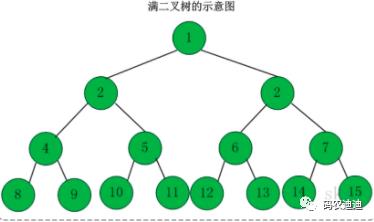
满二叉树:
一棵深度为k 且有2k -1个结点的二叉树。(特点每层都“充满”了结点)
完全二叉树:
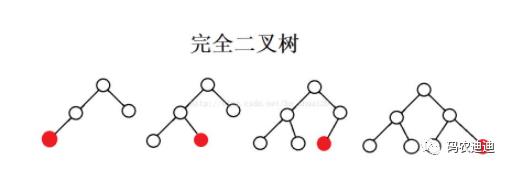
性质4:具有n个结点的完全二叉树的深度必为[log2n]+1
证:2^(k−1)−1<n≤2^k−1或2^(k−1)≤n<2^k,推出k−1≤log2 n<k,因为k是整数,所以k=[log2 n]+1
性质5:对完全二叉树,若从上至下,从左至右编号,则编号为i的结点,其左孩子编号必为2i,其右孩子编号必为2i+1,其双亲的编号必为i/2。
例题:
设一棵完全二叉树具有1000个结点,则它有多少个叶子结点
法1:先求全部叶子数。n0=489(末层)+11(k-1层)=500个;
法2:先求2度结点数。n2=255(k-2层)+244(k-1层)=499个;
这两种方法的缺点:都要先计算树的深度 k=[log2 n]+1 =10;
法3:无需求树深k,便可快捷求出完全二叉树的叶子数:n0= n/2 // 取大于n/2的最小整数值 可由二叉树性质5轻松证明!(编号为i的结点,其孩子编号必为2i和2i+1)证:已知最后一个结点编号为n,则其双亲(n/2或(n-1)/2)肯定是最后一个非叶子结点。其编号之后的全部结点都是叶子了!故,n0=n-n/2或n-(n-1)/2=n/2
二叉树的链表储存表示
typedef struct BiTNode{int data;//左右子树struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;
树的遍历分为三种:前序遍历,中序遍历,后序遍历。
以前序遍历为例
(1)先遍历树根
(2)然后前序遍历左子树
(3)最后前序遍历右子树
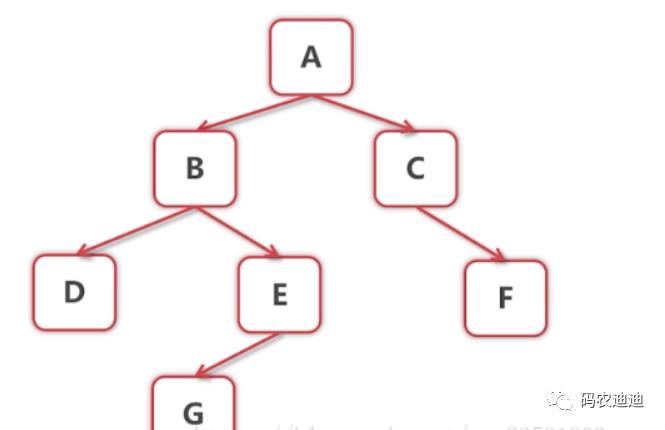
遍历流程:
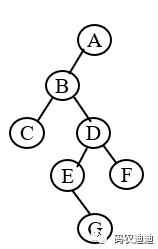
【1】首先遍历树根,输出A
【2】对A的左子树进行前序遍历,怎么前序遍历?对于B这个左子树而言,首先遍历根节点,输出B
【3】然后遍历子树B的左子树,得到D这个子树,对D进行前序遍历,首先遍历树根节点,输出D
【4】然后遍历D的左子树,不存在。那就遍历D的右子树,不存在。此时B的左子树D遍历完成
【5】遍历B的右子树E,则前序遍历E,首先遍历树根结点,输出E
【6】遍历E的左子树,得到子树G,对于子树G,前序遍历G,得到树根节点G,输出G,此时G遍历完成
【7】此时A的左子树遍历完成,现在开始遍历A的右子树C,前序遍历C,得到树根结点,输出C
【8】遍历C的左子树,不存在,则遍历其右子树,得到子树F,前序遍历F,得到树根结点F,输出F
于是结果为 :ABDEGCF
前序遍历
int PreOrderTraverse(BiTree T){if(T==NULL) return OK; //空二叉树else{cout<<T->data; //访问根结点PreOrderTraverse(T->lchild); //递归遍历左子树PreOrderTraverse(T->rchild); //递归遍历右子树}}
同理可得中序遍历
int InOrderTraverse(BiTree T){if(T==NULL) return OK; //空二叉树else{InOrderTraverse(T->lchild); //递归遍历左子树cout<<T->data; //访问根结点InOrderTraverse(T->rchild); //递归遍历右子树}}
后序遍历
int PostOrderTraverse(BiTree T){if(T==NULL) return OK; //空二叉树else{PostOrderTraverse(T->lchild); //递归遍历左子树PostOrderTraverse(T->rchild); //递归遍历右子树cout<<T->data; //访问根结点}}
二叉树的建立(由先序遍历结果建立)
A B C ##D E#G##F###
void CreateBiTree(BiTree &T){cin>>ch;//递归结束,建空树if (ch=='#') T=NULL;else{//生成根结点T=new BiTNode; T->data=ch;//递归创建左子树CreateBiTree(T->lchild);//递归创建右子树CreateBiTree(T->rchild);}}
计算二叉树结点总数
思路:如果是空树,则结点个数为0;
否则,结点个数为左子树的结点个数+右子树的结点个数再+1。
int NodeCount(BiTree T){if(T == NULL ) return 0;else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;}
计算叶子结点个数
思路:如果是空树,则叶子结点个数为0;
否则,为左子树的叶子结点个数+右子树的叶子结点个数。
int LeadCount(BiTree T){//如果是空树返回0if(T==NULL) return 0;//如果是叶子结点返回1if (T->lchild == NULL && T->rchild == NULL)return 1; //如果是叶子结点返回1else return LeafCount(T->lchild) + LeafCount(T->rchild);}
计算二叉树的深度
思路:如果是空树,则深度为0;
否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1。
int depthCount(BiTree *T){if (T==NULL) return 0;//返回较大者加1else return max(depthCount(T->lchild),depthCount(T->rchild))+1;}
由中序遍历与后序遍历确定前序遍历
#include<cstdio>#include<iostream>#include<cstring>using namespace std;//in为中序排列 after为后序排列void beford(string in,string after){if (in.size()>0){//后序排列的第一个为根char ch=after[after.size()-1];//找根输出cout<<ch;//在中序排列中找到位置 递归调用左子树与右子树int k=in.find(ch);//substr第一个参数为截取的起始位,第二个参数为长度beford(in.substr(0,k),after.substr(0,k));beford(in.substr(k+1),after.substr(k,in.size()-k-1));}}int main(){string inord,aftord;cin>>inord;cin>>aftord;//读入beford(inord,aftord);cout<<endl;return 0;}
由前序遍历与中序遍历求后序遍历
#include<iostream>#include<string>using namespace std;string str1,str2;//先中序 后前序void maketree(string s,string t){//长度为零直接返回if(!(int)t.size()) return;//前序排列的第一个为根char ch=t[0];//在中序遍历中找到根int k=s.find(ch);maketree(s.substr(0,k),t.substr(1,k));//递归左子树maketree(s.substr(k+1),t.substr(k+1));//递归右子树//最后输出根cout<<ch;}int main(){cin>>str1>>str2;maketree(str1,str2);return 0;}

以上是关于数据结构之树(二叉树)的探索的主要内容,如果未能解决你的问题,请参考以下文章