力扣每日一题打卡 - 构建二叉树专题

Posted 2021-04-09 工程师Ruojhen

这道题是今天（2020-09-25）力扣官方的每日一题， 之前我写了题解，总结了 《构建二叉树专题》^{[1]（可以阅读原文查看）}。有一些朋友说我的复杂度有点高，实际上我只是为了新手容易理解才那么写的， 今天稍微修改一下放给大家看。

此题目和105. 从前序与中序遍历序列构造二叉树^[2] 完全一致，如果你会其中一个，那么另外一个也一定会。

我们以题目给出的测试用例来讲解：

后序遍历是左右根，因此postorder最后一个元素一定整个树的根。由于题目说明了没有重复元素，因此我们可以通过val去inorder找到根在inorder中的索引i。而由于中序遍历是左根右，我们容易找到i左边的都是左子树，i右边都是右子树。

我使用红色表示根，蓝色表示左子树，绿色表示右子树。

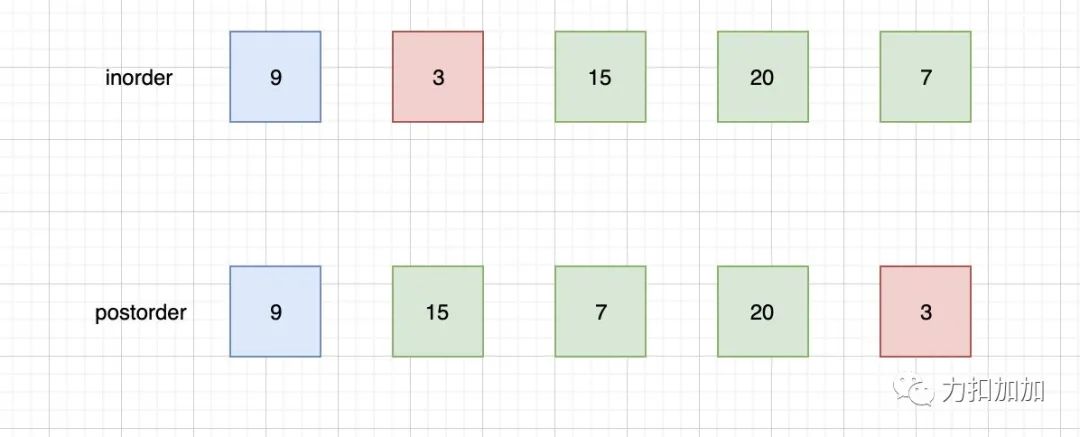
根据此时的信息，我们能构造的树是这样的：

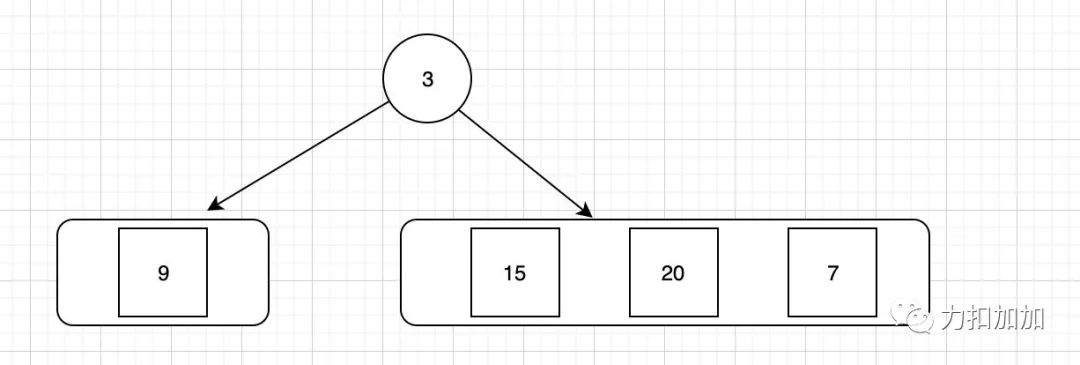
其中右子树由于个数大于1，我们无法确定，我们继续执行上述逻辑。我们postorder继续向前移动一位，这个时候我们得到了第二个根节点”20“，实际上就是右子树的根节点。

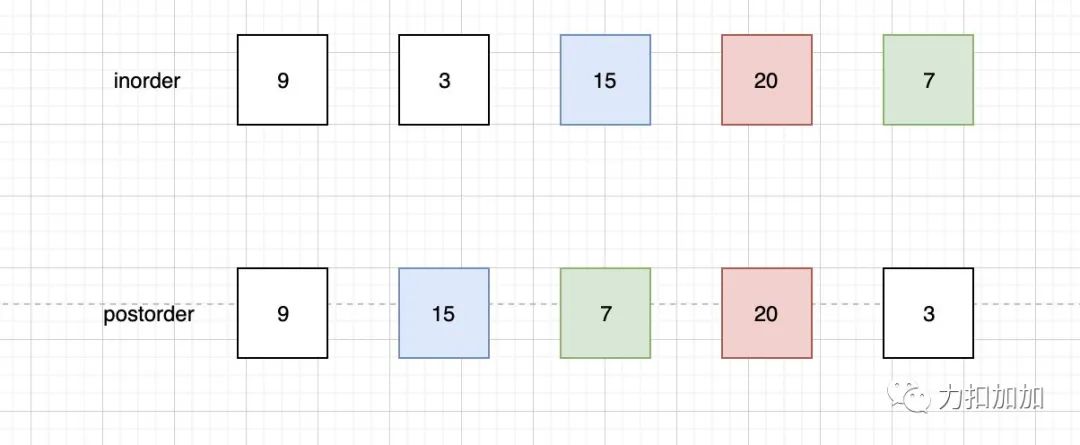
根据此时的信息，我们能构造的树是这样的：

我们不断执行上述逻辑即可。

代码：

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        # 实际上inorder 和 postorder一定是同时为空的，因此你无论判断哪个都行
        if not inorder:
            return None
        root = TreeNode(postorder[-1])
        i = inorder.index(root.val)
        root.left = self.buildTree(inorder[:i], postorder[:i])
        root.right = self.buildTree(inorder[i+1:], postorder[i:-1])

        return root

简单起见，递归的时候每次我都开辟了新的数组，这个其实是没有必要的，我们可以通过四个变量来记录inorder和postorder的起始位置即可， 具体见下方代码区。

代码

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        def dfs(inorder, in_start, in_end, postorder, post_start, post_end):
            if in_start > in_end: return None
            if in_start == in_end: return TreeNode(inorder[in_start])
            if post_start == post_end: return TreeNode(inorder[in_start])
            root = TreeNode(postorder[post_end])
            i = inorder.index(root.val)
            root.left = dfs(inorder, in_start, i - 1, postorder, post_start, post_start + i - 1 - in_start)
            root.right = dfs(inorder, i + 1, in_end, postorder, post_start + i - 1 - in_start + 1, post_end - 1)
            return root
        n = len(inorder)
        return dfs(inorder, 0, n - 1, postorder, 0, n - 1)

「复杂度分析」

• 时间复杂度：由于每次递归我们的inorder和postorder的总数都会减1，因此我们要递归N次，故时间复杂度为  ，其中N为节点个数。
• 空间复杂度：我们使用了递归，也就是借助了额外的栈空间来完成， 由于栈的深度为N，因此总的空间复杂度为  ，其中N为节点个数。

Reference

[1] 

构建二叉树专题: https://lucifer.ren/blog/2020/02/08/%E6%9E%84%E9%80%A0%E4%BA%8C%E5%8F%89%E6%A0%91%E4%B8%93%E9%A2%98/

[2] 

105. 从前序与中序遍历序列构造二叉树: https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/si-lu-qing-xi-dai-ma-jian-ji-he-105ti-si-lu-yi-z-2/

推荐阅读

1、

2、

3、

4、

5、

如果觉得文章不错，帮忙点个在看呗