下次再让你讲平衡二叉树，可别说不会了

Posted 2021-04-09 波波Tea

我前面写过一篇文章，是关于二叉查找树的结点插入的，详情请戳这里 ，并且在最后我揭露了这种插入算法的弊端，就是会导致树不平衡，而树越不平衡，查找操作的时间复杂度就越高，这显然是一种坏的插入算法。

今天我要讲的知识，就是来解决这个问题的。

平衡二叉树基本概念

平衡二叉树，也是一种二叉查找树，但它是平衡的，即左子树与右子树的高度差最多等于1。

平衡二叉树也叫AVL树，取自发明平衡二叉树算法的人的人名。

平衡因子BF：左子树深度减去右子树深度的值。平衡二叉树所有结点的平衡因子只能是-1,0,1。

最小不平衡子树：假设新插入了一个结点A，然后导致树不平衡了，距离结点A最近且BF绝对值大于1的那个结点为B，以B结点为根的树称为最小不平衡子树

平衡二叉树实现原理

在构建二叉查找树过程中，每插入一个结点，先检查是否破坏了树的平衡。若是，则找出最小不平衡子树，在保持二叉查找树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之达到新的平衡。

旋转分两种：左旋和右旋。右旋会减小BF，左旋增加BF。

上面的说辞比较抽象，下面就来具体一点的。为了更好地讲解原理，我们以依次插入结点3,2,1,4,5,6,7,10,9,8为例。

第一步

首先插入3和2是没问题的。

第二步

当插入1时，发现结点3的BF变成了2，因此需要右旋，如下图所示。

     

第三步

插入4没问题。

第四步

当插入5时，结点3的BF变成了-2，因此左旋。

第五步

当插入结点6时，结点2的BF变成了-2，将根结点左旋。但3有点多余，将它设置为结点2的右孩子。

大家有没有担心这种情况：结点4的左子树，不单单是一个结点，而是一颗高度大于1的子树？其实不会的，它只能是一个结点。大家可以用笔在纸上画一下，平衡二叉树不会出现这样的情况。

第六步

当插入结点7时，结点5的BF变成-2，左旋。

第七步

插入10没问题。

第八步

当插入9时，7的BF为-2，理论上左旋就行了，但会不满足二叉查找树的特性。

导致这种情况的原因是：结点7和它的孩子结点10，两者的BF符号不一致。既然不一致，先将结点9和结点10组成的子树右旋，然后再以结点7为根结点进行左旋。

第九步

当插入结点8时，结点6的BF为-2，而结点9的BF为1，为了保证符号统一，因此以结点9为根结点进行右旋，注意，结点8本来是结点7的右孩子，但是右旋之后，因为7<8<9，所以只能将结点8当成结点9的左孩子。

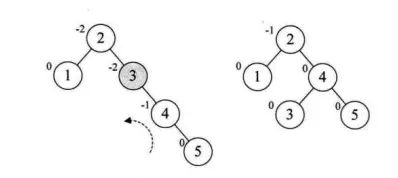
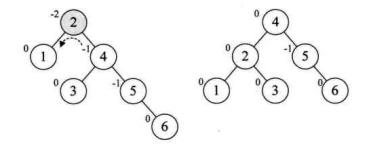
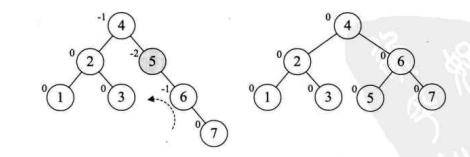
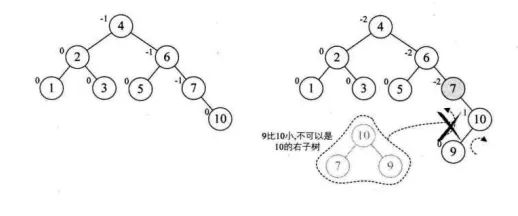
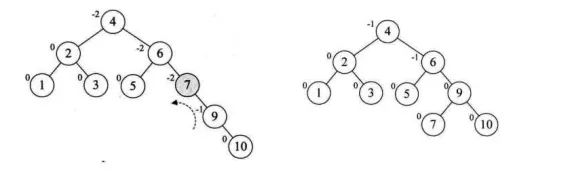
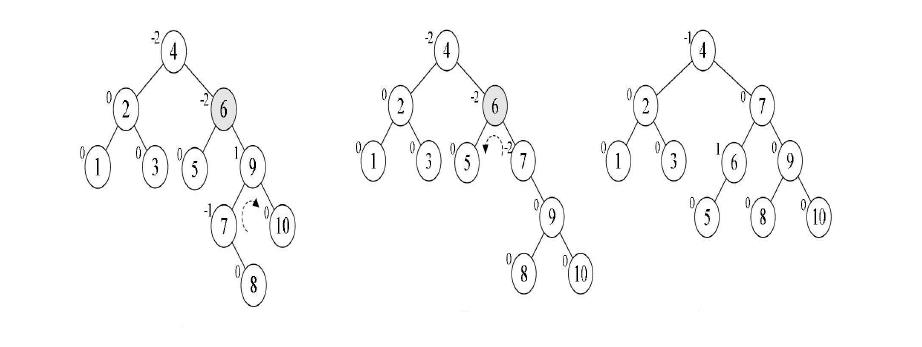
平衡二叉树代码实现

平衡二叉树实现原理中的九个步骤，是代码实现的铺垫 ，建议大家将九个步骤都看懂，然后再看代码，这九个步骤几乎涵盖了所有可能的情况。

完整代码我已经上传到我的码云git仓库上了，如果就需要的话请访问我的码云git仓库获取，附上地址：https://gitee.com/bobo_tea/datastructure/tree/master/src/main/datastructure/com/bobo/group/tree/avl。或者点击公众号底部菜单->资源汇总->仓库汇总。或者联系我。

我的平衡二叉树实现分四个类：

Ancestor：祖先类

AVLInsert：平衡二叉树结点插入核心实现

AVLMain：main方法所在类，包含示例程序

AVLNode：avl树结点类

AVLNode

import com.bobo.group.tree.draw.Drawable;

public class AVLNode implements Drawable {
    private int val;
    private AVLNode left;
    private AVLNode right;

    public AVLNode(int val) {
        this.val = val;
    }

    public AVLNode(int val, AVLNode left, AVLNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }

    //省略getter/setter方法

    @Override
    public String getValue() {
        return String.valueOf(this.val);
    }

    @Override
    public Drawable getLeftNode() {
        return this.left;
    }

    @Override
    public Drawable getRightNode() {
        return this.right;
    }
}

Ancestor

/**
 * 结点的祖先信息
 */
public class Ancestor {
    private AVLNode ancestor;
    private boolean isLeft;

    public Ancestor(AVLNode ancestor) {
        this.ancestor = ancestor;
    }

    public Ancestor(AVLNode ancestor, boolean isLeft) {
        this.ancestor = ancestor;
        this.isLeft = isLeft;
    }
    // 省略getter/setter方法
}

AVLInsert

import com.bobo.group.common.CommonUtil;
import com.bobo.group.tree.draw.DrawTree;
import java.util.ArrayList;
import java.util.List;

public class AVLInsert {
    //记录插入的每个结点
    private List<AVLNode> avlNodes = new ArrayList<>();
    //画二叉树对象
    private DrawTree drawTree = new DrawTree();
    //可变的根结点，因为根结点也会旋转
    private AVLNode variableRoot;
    //生成图片时计数
    private int drawCounter=1;
    //树偏移量数组，画图用
    //private int[] offset_x_arr = new int[]{60,30,25,20,20,20,10,10};
    private int[] offset_x_arr = new int[]{120,80,30,30,20,20,10,10};

    /**
     * 每插入一个结点，就画一次图
     * @param key
     */
    private void drawStep(int key){
        drawTree.drawEntrance(variableRoot, CommonUtil.getResourceRoot()+"tree/avl/avlinsert_"+drawCounter+"_"+key+".png",false,offset_x_arr);
        drawCounter++;
    }

    /**
     * 平衡二叉树插入结点核心算法
     * @param avlNode 当前结点
     * @param key 要插入的关键字
     * @param ancestorChain 祖先信息链
     */
    private void insert(AVLNode avlNode,int key,List<Ancestor> ancestorChain){
        if(key < avlNode.getVal()){
            //新增一个祖先信息
            ancestorChain.add(new Ancestor(avlNode,true));
            //左孩子为null，则执行插入
            if(avlNode.getLeft() == null){
                AVLNode keyNode = new AVLNode(key);
                avlNodes.add(keyNode);
                avlNode.setLeft(keyNode);
                //平衡算法
                calculateBFAndRotate(ancestorChain);
                //平衡后，画图
                drawStep(key);
                return;
            }else{
                //递归搜索
                insert(avlNode.getLeft(),key,ancestorChain);
            }
        }

        if(key > avlNode.getVal()){
            //新增一个祖先信息
            ancestorChain.add(new Ancestor(avlNode,false));
            //右孩子为null，则执行插入
            if(avlNode.getRight() == null){
                AVLNode keyNode = new AVLNode(key);
                avlNodes.add(keyNode);
                avlNode.setRight(keyNode);
                //平衡算法
                calculateBFAndRotate(ancestorChain);
                //平衡后，画图
                drawStep(key);
                return;
            }else{
                //递归搜索
                insert(avlNode.getRight(),key,ancestorChain);
            }
        }

    }

    /**
     * 计算平衡因子，如果有必要的话，还要旋转
     * @param ancestorChain 祖先链
     */
    private void calculateBFAndRotate(List<Ancestor> ancestorChain){
        //ancestorChain持有的都是新插入的那个导致树不平衡的结点的祖先
        // 祖先的顺序是：index为0时，为距离最远的祖先，index为size-1时，为距离最近的祖先
        //所以，如果我们要找出最小不平衡子树，则需要从最近的祖先开始判断
        for (int i = ancestorChain.size()-1;i >= 0;i--){
            //当前祖先
            AVLNode ancestorNode = ancestorChain.get(i).getAncestor();
            boolean leftOfAncestor = ancestorChain.get(i).isLeft();

            //分别计算当前祖先的左右子树深度
            int leftDepth = searchDepth(ancestorNode.getLeft(),1);
            int rightDepth = searchDepth(ancestorNode.getRight(),1);
            //计算当前祖先的平衡因子
            int bf = leftDepth-rightDepth;
            //如果bf绝对值大于1，则表示树不平衡，需要进行相应的处理；否则，不做任何事情
            if(Math.abs(bf) > 1){
                //先判断当前祖先的子节点 与 当前祖先 的BF符号是否一致
                AVLNode child = leftOfAncestor?ancestorNode.getLeft():ancestorNode.getRight();
                int childLeftDepth = searchDepth(child.getLeft(),1);
                int childRightDepth = searchDepth(child.getRight(),1);
                int childBf = childLeftDepth-childRightDepth;

                //符号不一致，以子结点为根结点进行旋转
                if(childBf > 0 && bf < 0){
                    //右旋，旋转一个单位即可，应该没有特殊情况
                    rightRotate(ancestorNode,child,leftOfAncestor);
                }else if(childBf < 0 && bf > 0){
                    //左旋
                    leftRotate(ancestorNode,child,leftOfAncestor);
                }
                //符号统一之后，再旋转当前结点
                if(bf > 0){
                    // 右旋
                    if(i == 0){
                        //根结点的旋转特殊处理
                        AVLNode rootLeftRight = ancestorNode.getLeft().getRight();
                        AVLNode rootLeft = ancestorNode.getLeft();
                        rootLeft.setRight(ancestorNode);
                        ancestorNode.setLeft(rootLeftRight);
                        //更新可变根结点
                        variableRoot = rootLeft;
                    }else{
                        //非根结点处理，将当前祖先的父节点，当前祖先，当前祖先与其父节点的关系传给rightRotate方法
                        rightRotate(ancestorChain.get(i-1).getAncestor(),ancestorNode,ancestorChain.get(i-1).isLeft());
                    }

                }else if(bf < 0){
                    // 左旋
                    if(i == 0){
                        //根结点的旋转特殊处理
                        AVLNode rootRightLeft = ancestorNode.getRight().getLeft();
                        AVLNode rootRight = ancestorNode.getRight();
                        rootRight.setLeft(ancestorNode);
                        ancestorNode.setRight(rootRightLeft);
                        //更新可变根结点
                        variableRoot = rootRight;
                    }else{
                        //非根结点处理，将当前祖先的父节点，当前祖先，当前祖先与其父节点的关系传给rightRotate方法
                        leftRotate(ancestorChain.get(i-1).getAncestor(),ancestorNode,ancestorChain.get(i-1).isLeft());
                    }

                }

            }
        }
    }

    //左旋时，防止右节点的左孩子不为空
    private void leftRotate(AVLNode parent,AVLNode node,boolean isLeft){
        //由于是左旋，为了避免不满足二叉查找树特性，所以要先判断node的右孩子的左孩子是否为null
        AVLNode nodeRightLeft = node.getRight().getLeft();
        if(isLeft){
            parent.setLeft(node.getRight());
            parent.getLeft().setLeft(node);
            node.setRight(nodeRightLeft);
        }else{
            parent.setRight(node.getRight());
            parent.getRight().setLeft(node);
            node.setRight(nodeRightLeft);
        }
    }

    //右旋时，防止左节点的右孩子不为空
    private void rightRotate(AVLNode parent,AVLNode node,boolean isLeft){
        //由于是右旋，为了避免不满足二叉查找树特性，所以要先判断node的左孩子的右孩子是否为null
        AVLNode nodeLeftRight = node.getLeft().getRight();
        if(isLeft){
            parent.setLeft(node.getLeft());
            parent.getLeft().setRight(node);
            node.setLeft(nodeLeftRight);
        }else{
            parent.setRight(node.getLeft());
            parent.getRight().setRight(node);
            node.setLeft(nodeLeftRight);
        }

    }

    //查找树的深度
    private int searchDepth(AVLNode avlNode, int depth){
        if(avlNode == null){
            return 0;
        }
        if(avlNode.getLeft() == null && avlNode.getRight() == null){
            return depth;
        }else if(avlNode.getLeft() == null){
            return searchDepth(avlNode.getRight(),depth+1);
        }else if(avlNode.getRight() == null){
            return searchDepth(avlNode.getLeft(),depth+1);
        }else{
            int a = searchDepth(avlNode.getLeft(),depth+1);
            int b = searchDepth(avlNode.getRight(),depth+1);
            return a>b?a:b;
        }
    }


    /**
     * 平衡二叉树结点插入入口
     * @param root 根结点
     * @param keys 要插入的关键字数组
     */
    public void insertEntrance(AVLNode root,int[] keys){

        if(null == root){
            root = new AVLNode(keys[0]);
            variableRoot = root;
            this.avlNodes.add(root);
            for (int i = 1; i < keys.length; i++) {
                List<Ancestor> parentPoints = new ArrayList<>();
                insert(variableRoot,keys[i],parentPoints);
            }
        }else{
            variableRoot = root;
            for (int i = 0; i < keys.length; i++) {
                List<Ancestor> parentPoints = new ArrayList<>();
                insert(variableRoot,keys[i],parentPoints);
            }
        }
    }

}

AVLMain

public class AVLMain {
    public static void main(String[] args) {
        AVLInsert avlInsert = new AVLInsert();
        avlInsert.insertEntrance(null,new int[]{3,2,1,4,5,6,7,10,9,8});
    }
}

运行main方法，我将每一步的结果生成了图片，供大家参考，暂时我还没测出bug来，应该没啥问题。

平衡二叉树应该还挺重要的，它的算法有一定难度，不过掌握了思想之后，代码写起来就很快了。

今天就讲到这里了，明天的文章将开启新的知识。不过还是树。