数据结构二叉树

Posted 2021-04-09 分享电脑学习

二叉树遍历的概念

二叉树遍历是指按照一定次序访问二叉树中所有结点，并且每个结点仅被访问一次的过程。

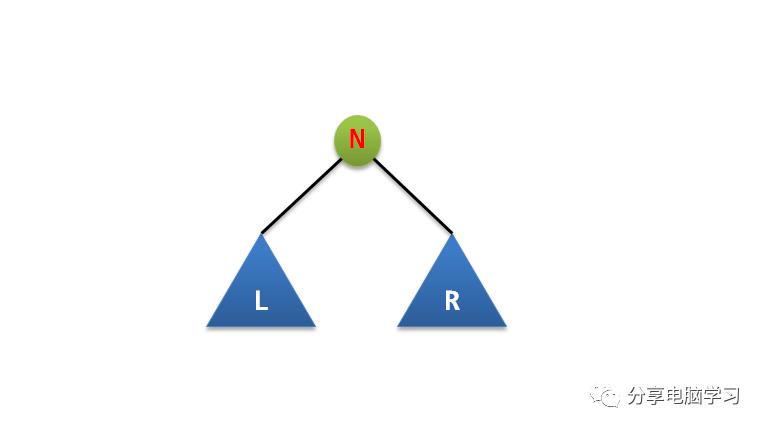
设N为根结点，L、R分别为左、右子树，这6种遍历方法是NLR、LNR、LRN、NRL、RNL、RLN），若再规定先遍历左子树，后遍历右子树，则对于非空二叉树，可得到如下3种递归的遍历方法（即NLR、LNR和LRN）。

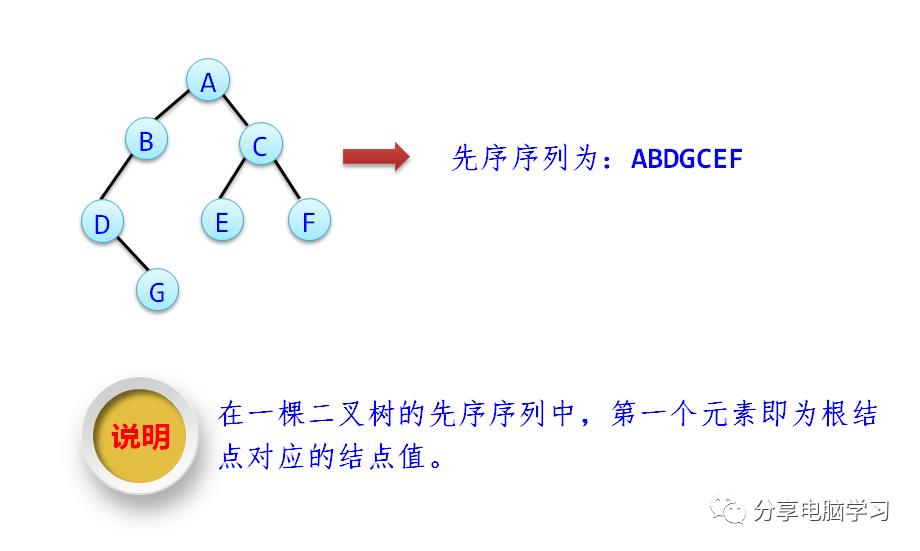
1）先序遍历

① 访问根结点。

② 先序遍历左子树。

③ 先序遍历右子树。

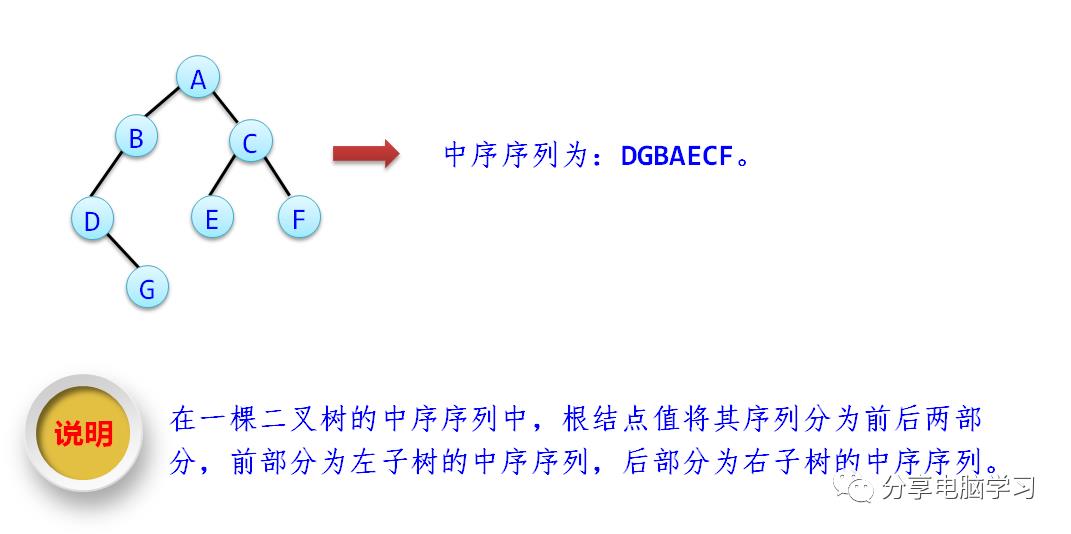
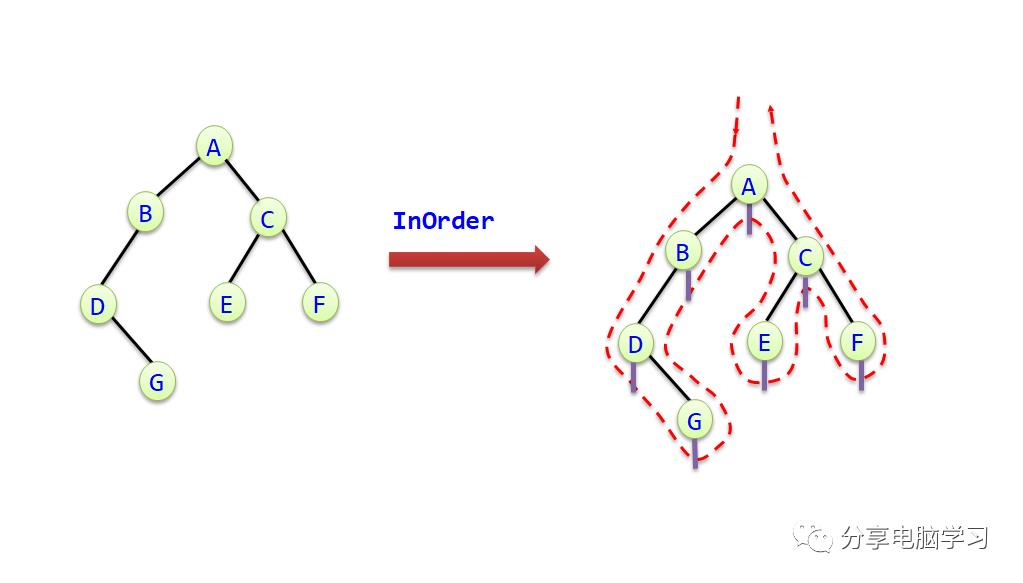
2）中序遍历

① 中序遍历左子树。

② 访问根结点。

③ 中序遍历右子树。

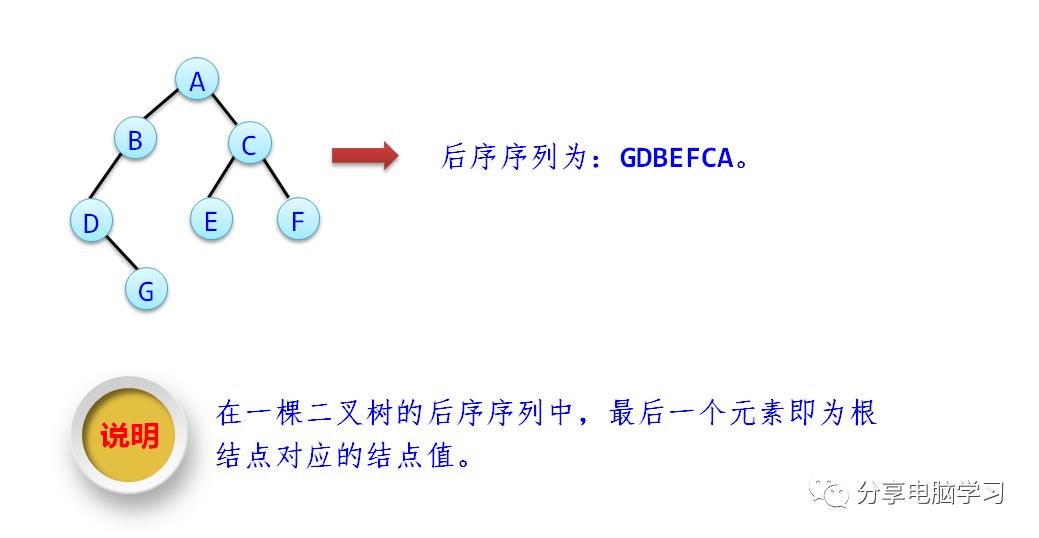
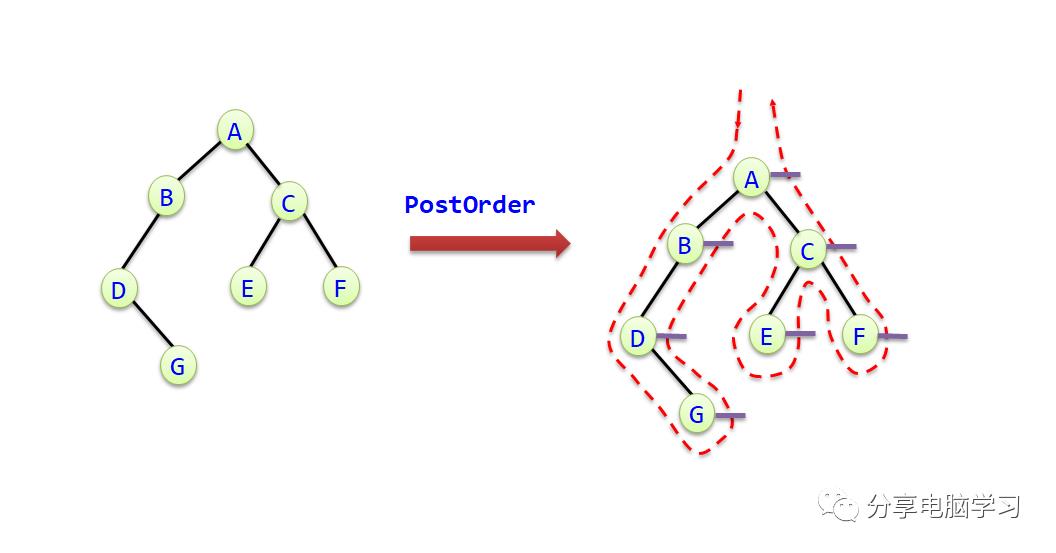
3）后序遍历

① 后序遍历左子树。

② 后序遍历右子树。

③ 访问根结点。

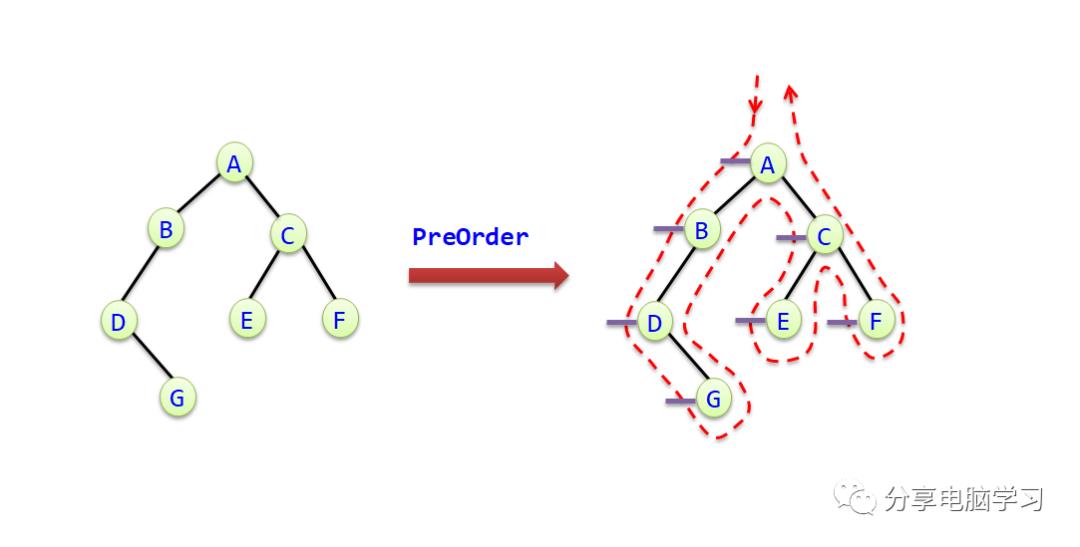
先序、中序和后序遍历递归算法

1）先序遍历的递归算法

2）中序遍历的递归算法

3）后序遍历的递归算法

递归遍历算法的应用

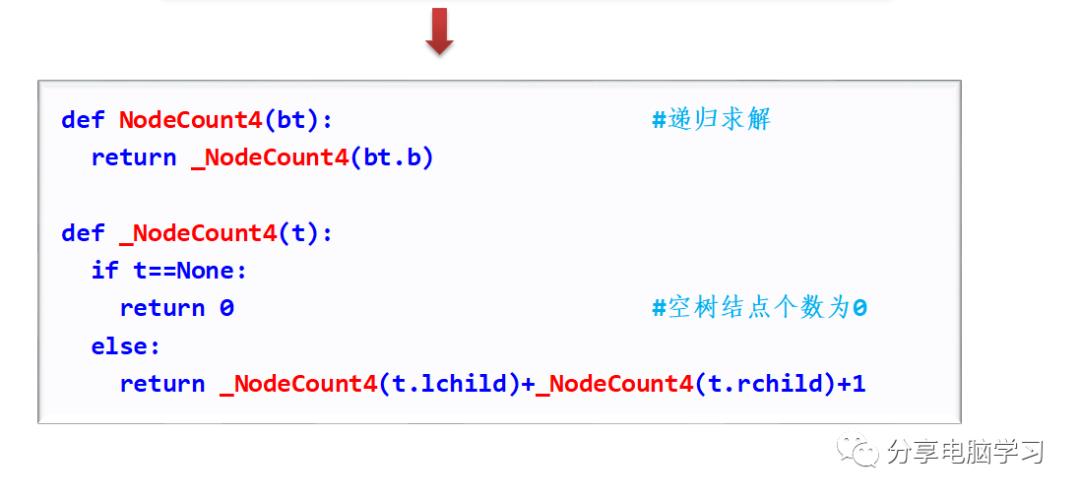
假设二叉树采用二叉链存储结构存储，设计一个算法求一棵给定二叉树中的结点个数。

解：求一棵二叉树中的结点个数是以遍历算法为基础的，任何一种遍历算法都可以出一棵二叉树中的结点个数。

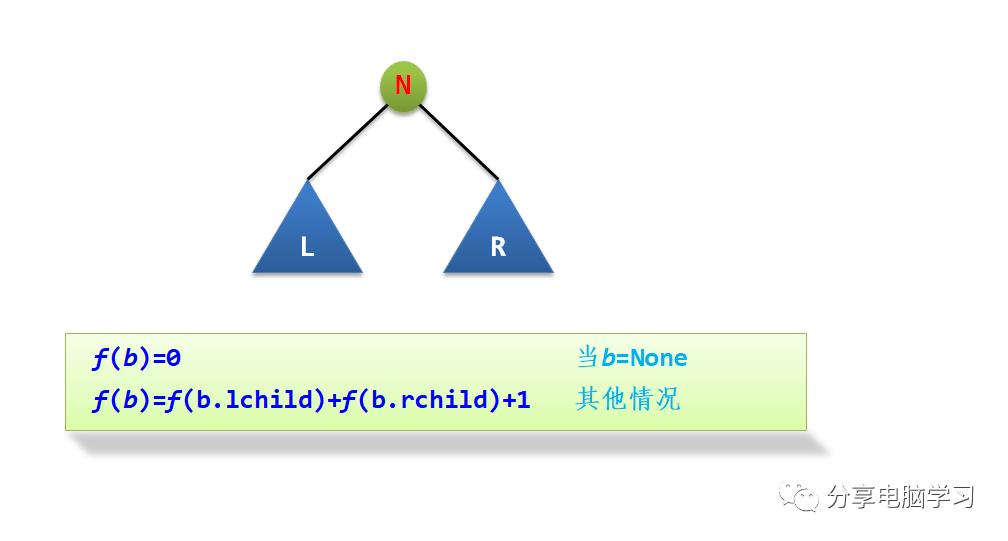
也可以从递归算法设计的角度来求解。设f(b)求二叉树b中所有结点个数，它是“大问题”，f(b.lchild)和f(b.rchild)分别求左、右子树的结点个数。

假设二叉树采用二叉链存储结构存储，设计一个算法按从左到右输出一棵二叉树中所有叶子结点值。

    解：由于先序、中序和后序递归遍历算法都是按从左到右的顺序访问叶子结点的，所以本题可以基于这三种递归遍历算法求解。

也可以直接采用递归算法设计方法求解。

设f(b)的功能是从左到右输出以b为根结点的二叉树的所有叶子结点值，为“大问题”，显然f(b.lchild)和f(b.rchild)是两个“小问题”。

当b不是叶子结点时，先调用f(b.lchild)再调用f(b.rchild)。

对应的递归模型f(b)如下：

从上述两例看出，基于递归遍历思路和直接采用递归算法设计方法完全相同。实际上，当求解问题较复杂时，直接采用递归算法设计方法更加简单方便。

仅从递归遍历角度看，上述两例基于3种递归遍历思路中任意一种都是可行的，但有些情况并非如此。

一般地，二叉树由根、左右子树3部分构成，但可以看成两类，即根和子树。

如果需要先处理根再处理子树，可以采用先序遍历思路。

如果需要先处理子树，再处理根，可以采用后序遍历思路。

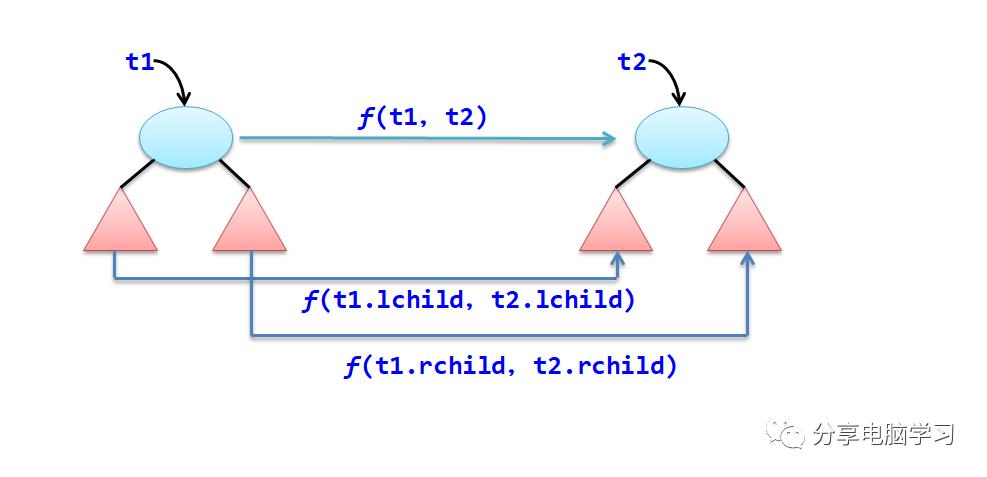
假设二叉树采用二叉链存储结构存储，设计一个算法将二叉树bt1复制到二叉树bt2。

解：采用直接递归算法设计方法。设f(t1，t2)是由二叉链t1复制产生t2，这是“大问题”。

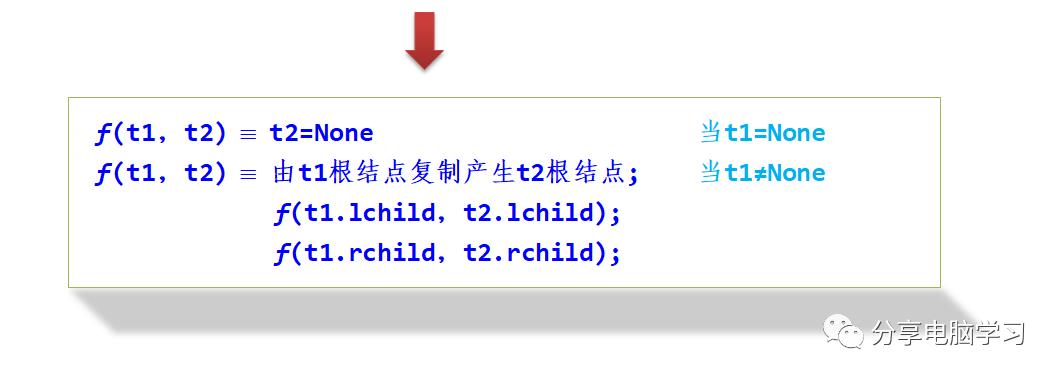
也可以采用基于后序遍历思路

假设一棵二叉树采用二叉链存储结构，且所有结点值均不相同，设计一个算法求二叉树中指定结点值的结点所在的层次（根结点的层次计为1）

解:

二叉树中每个结点都有一个相对于根结点的层次，根结点的层次为1，那么如何指定这种情况呢？

可以采用递归算法参数赋初值的方法，即设f(b，x，h)为“大问题”，增加第3个参数h表示第一个参数b指向结点的层次，在初始调用时b指向根结点，h对应的实参为1，从而指定了根结点的层次为1的情况。

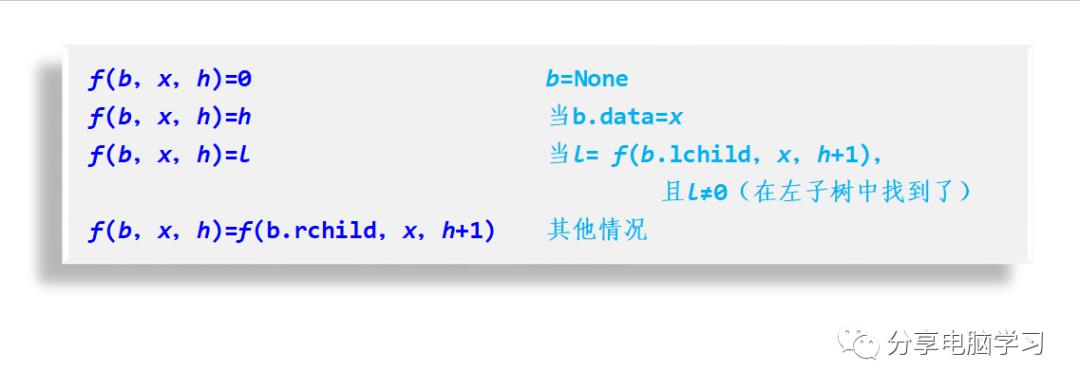
递归算法参数赋初值问题

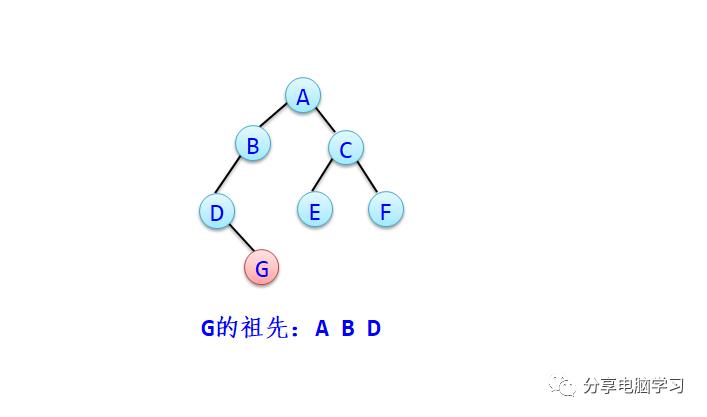
假设二叉树采用二叉链存储结构，且所有结点值均不相同，设计一个算法输出值为x的结点的所有祖先。

解法1

根据二叉树中祖先的定义可知，若一个结点的左孩子或右孩子值为x时，则该结点是x结点的祖先结点；若一个结点的左孩子或右孩子为x结点的祖先结点时，则该结点也为x结点的祖先结点。

设f(t，x)表示t结点是否为x结点的祖先结点。

解法2

二叉树中x结点的祖先恰好是根结点到x结点的路径上除了x结点外的所有结点，用全局变量res列表表示。

采用先序遍历的思路，采用一个path列表存放路径，当找到x结点时，将path中x结点（最后添加的结点）删除，再将path复制的ans中。

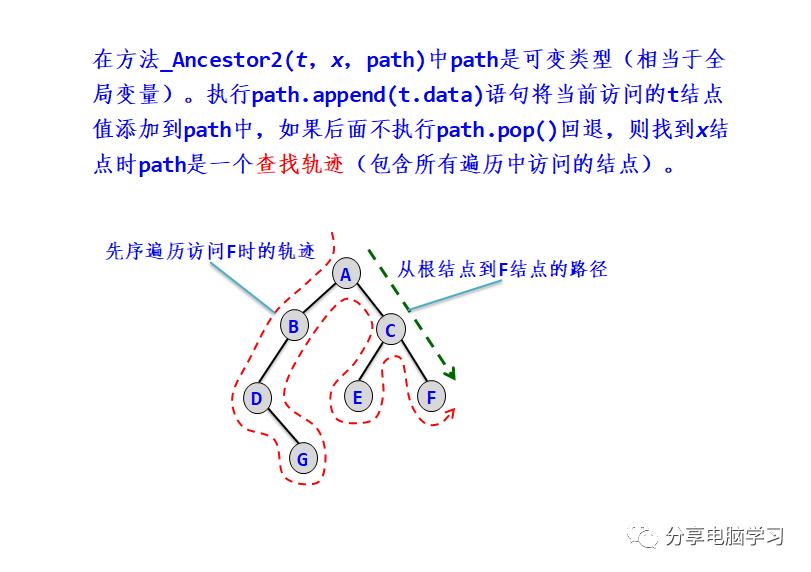
改进算法2：

改为用path[0..d]存放根到x结点的路径