生活中的数学——葡萄酒与二叉树

Posted 2021-04-09 白水的数学小天地

在上一期内容中，笔者为大家介绍了葡萄酒投资的基本原理，并引入了布朗运动模型（即维纳过程）作为葡萄酒期权的定价依据。在这一期内容中，笔者就带领大家看看，当“葡萄酒”遇到“二叉树”，二者又会擦出什么样的火花呢？

在这篇文章中，“葡萄酒”并非用来饮用的葡萄酒商品，而是用于投资的葡萄酒期权；“二叉树”也并非真正的树，而是用于确定期权产品价格的定价模型。二叉树模型是未定权益定价最简单、也是最直接的方法。

在二叉树模型问世之前，就已经有人对期权类产品的定价问题产生一些想法了。1973年，布莱克和舒尔斯(Black and Scholes)针对连续时间下期权收益情况的变动，提出了Black-Scholes期权定价模型。这个模型认为，只有期权价格的现值会影响期权未来价格的预测值，而期权未来价格的预测与期权过去的价格无关。

Black-Scholes期权定价模型要求基础资产不支付红利，并且其价格严格服从几何布朗运动的变化规律，因此基础资产的价格可以用下面这个微分方程表示：

其中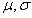为常数，为期权的价值，表示一个标准布朗运动。

假设期权的期限为T，用f(t,S_t)表示期权在时刻t的价格，根据Ito引理，我们可以得到f(t,S_t)的二阶偏导方程为：

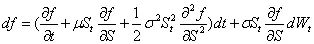
根据公式，得到Black-Scholes微分方程：

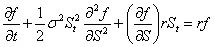    其中r为常数

Black-Scholes模型充分说明我们可以不考虑期权的价格变化过程以及期权的历史价值，而只用期权的当前价值预测其未来价格的变化趋势，并可以对欧式期权进行精确的定价。但美中不足的是，Black-Scholes期权定价模型考虑的变量过于复杂，合约期限、期权现值、利率水平都是影响期权未来价格的重要因素。在操作上，Black-Scholes模型需要考虑的变量太多，预测误差也会随变量的增加而增大。因此，二叉树模型问世了。

1979年，罗斯、考科斯和马克·鲁宾斯坦提出了一种简单的对离散时间的期权的定价方法，被称为Cox-Ross-Rubinstein二项式期权定价模型(CRR模型)。他们的作品被发表在《金融经济学杂志》上，并逐渐得到经济学界的认可。二项式期权定价模型和Black-Scholes期权定价模型，是两种相互补充的方法。

二项式期权定价模型建立在一个基本假设基础上，即在给定的时间间隔内，期权的价格运动有两个可能的方向：上涨或者下跌。这一假设把一个给定的时间段分为更小的时间单位，因此在面对多个复杂变量联合影响的期权产品时，二叉树模型显然更加合适。

CRR二叉树模型中期权价格上涨与下降的比例不随时间的变化而变化，可以用下图的过程表示。

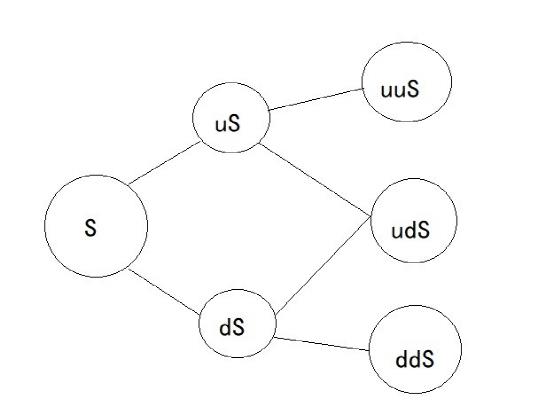
图中表示了一个两期二叉树的定价过程：当期权价格上升时，期权价格由S变为uS；而当期权价格下降时，价格变为dS。因此在i时刻点期权模型的定价为：

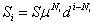
N_i是0时刻到i时刻股价上升的步数，是一个随机数，如此定义N_i表明在N时刻期权价格有N+1种状态而并非2^N种。在这种假设下，期权到期的支付与其价格变动路径无关，它仅仅依赖于期权价格上升和下降的步数，而不依赖于期权价格上升或下降的路径。

罗斯，考克斯和鲁宾斯坦根据二叉树模型定价的变化规律，推导出了期权的一般定价公式，即：

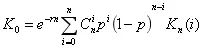
其中，K₀为期权定价的期望值，K_n(i)为期权在n时刻的价值，其中n时刻前有i次价格上升。

二叉树模型的优势在于计算期权的价格时并不依赖期权价格变化的路径，只需要得到期权价格的最终值，就可以计算出期权定价的期望。二叉树模型与Black-Scholes模型有异曲同工之妙，前者强调离散时间下期权的定价，而后者强调连续时间下的期权定价。

绝大部分葡萄酒交易的原则是在约定期限日或约定期限之前的任意一日执行交易，符合美式期权的特征。由于Black-Scholes模型无法对美式期权进行精确的定价，因此对葡萄酒期权的定价常用二叉树模型进行。在指定葡萄酒期权未来售出价格M_n(i)的情况下，我们可以根据CRR公式求出其定价：

在葡萄酒期权和其他的常用期权(比如股票)的定价与预测中，诸如二叉树和Black-Scholes的定价模型化无形为有形，变无序为有序，为投资盈利的实现奠定了十足的理论基础。数学模型就像影子跟着光一样，一直存在于我们的生活中。

扫描下方二维码可关注作者！