五分钟带你玩转平衡二叉树

Posted 2021-04-09 程序员的进击之路

通过上一篇二叉查找树的文章，相信大家已经掌握了二叉查找树的相关概念和操作，如果忘了可以通过下方的链接进行学习。带你玩转二叉查找树

本文呢，我们将在二叉查找树的基础上，继续学习一种新的树状结构-平衡二叉树。

我们已经有了二叉查找树，为什么还需要平衡二叉树呢？平衡二叉树到底缘起何处？

平衡二叉树的前世今生

在二叉查找树中，我们知道通过二叉查找树可以提高搜索效率，但是同一个序列，可以构成不同的二叉查找树形态，极端情况下(比如有序数组)，二叉查找树就会退变成一棵分化的左子树或者右子树，这个时候，相应的查找效率也直接变为O(n)。

比如上图中，有序数组[1,2,3,4,5,6,7,8]直接退变为一棵右子树，跟单链表一样了(比如我们查找元素8,需要比对8次)。

直观上来说，我们也不难想到: 二叉查找树的效率取决于树的高度，如果树的高度能够最小，那么即可保障查询效率。但到底该怎么才能做到呢?

每逢困境，总有英雄降临。平衡二叉树此时应运而生。

1962年，发明者 Adelson-Velsky 和 Landis 发表了论文，以两个作者的名字命名了该数据结构，这是较早发明的平衡二叉树 (故也叫AVL树)。

它是这样的一棵与众不同的树:

• 首先它是一棵二叉查找树。
• 任意一个节点的左右子树最大高度差为1( 树的高度，我们在树的基本介绍里面已经讲过了,忘了的小伙伴可以倒回去再看一看)。

说了这么说，可能大家还不是很明白, 下面我们上图:

平衡查找树和非平衡查找树的直观感受: 下图是同一个数组序列[1,2,3,4,5,6,7,8]的平衡二叉树和非平衡二叉树的表示

❝

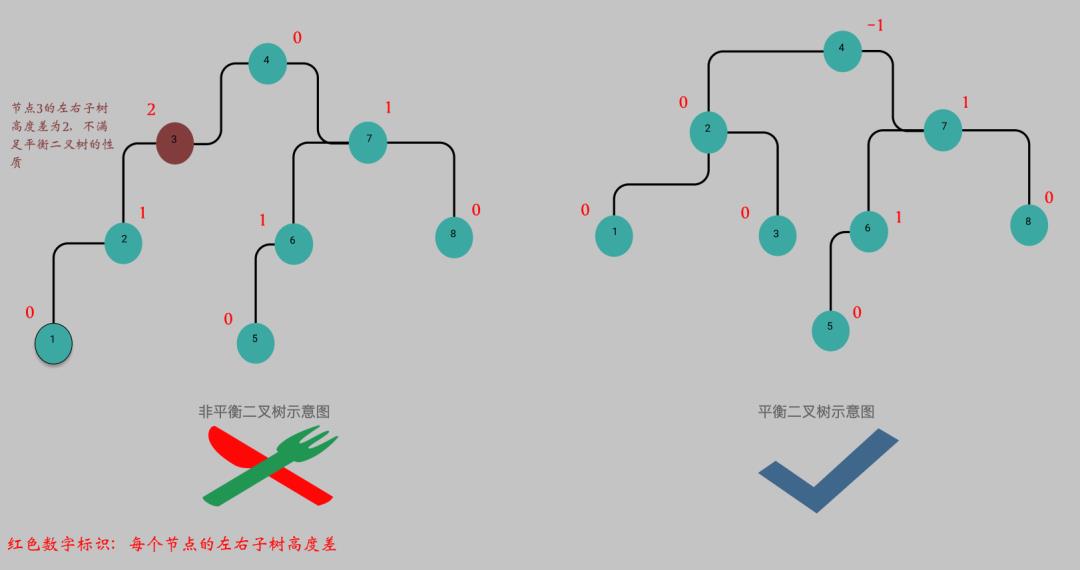
二叉树定义的两点都需满足才是平衡二叉树

平衡因子

通过上面的介绍，我们已经知道了平衡二叉树是什么了，这里我们也将重点介绍一下一个重要的概念-平衡因子。

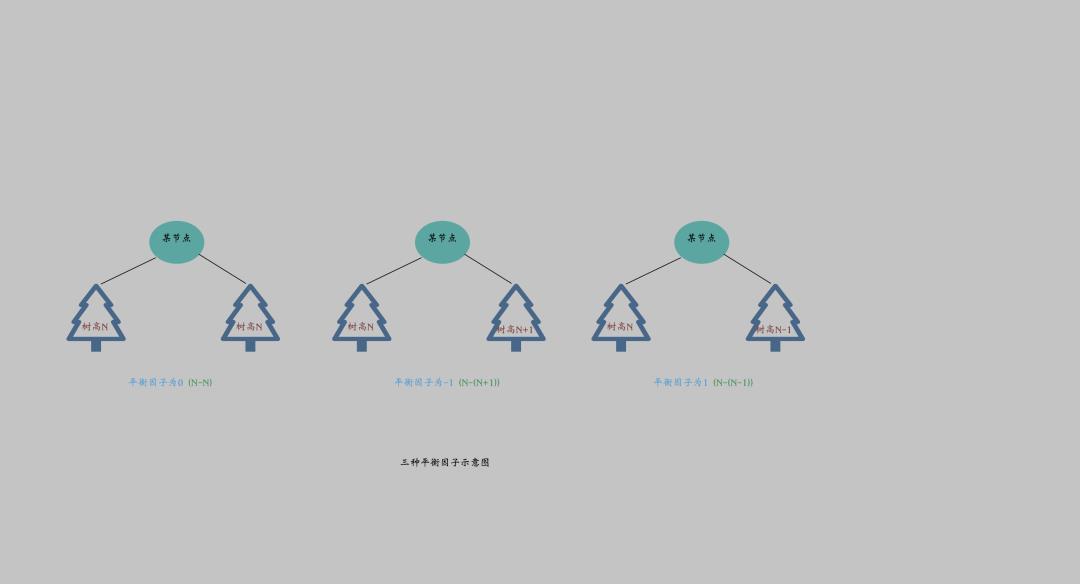
平衡因子: 平衡二叉树中某个节点的左子树和右子树的高度之差即为平衡因子。通过平衡二叉树的定义，我们知道每个节点的左右子树最大高度差为1，即平衡因子的取值只能为[-1, 0, 1]。

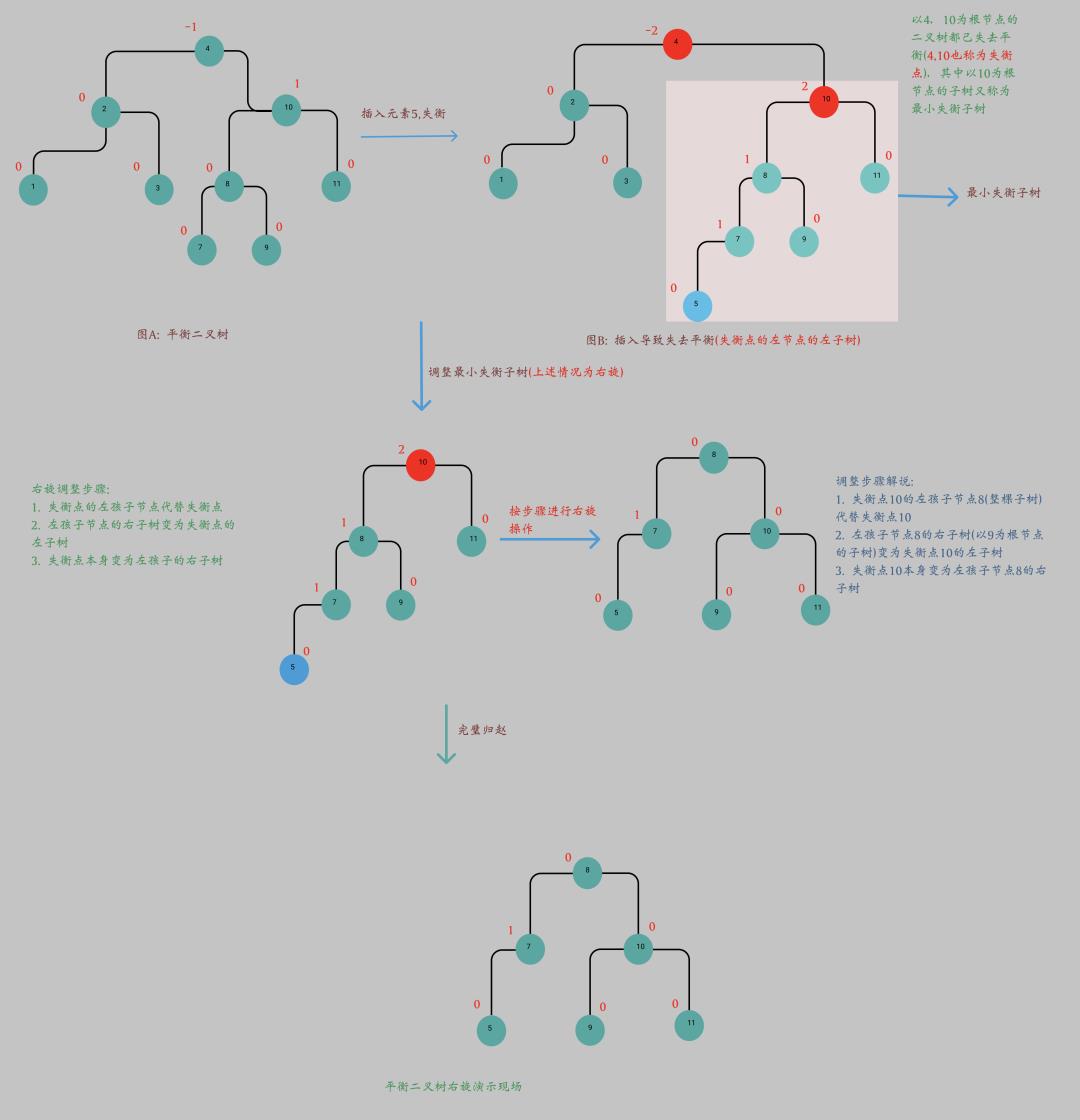
平衡二叉树失去平衡的前因后果

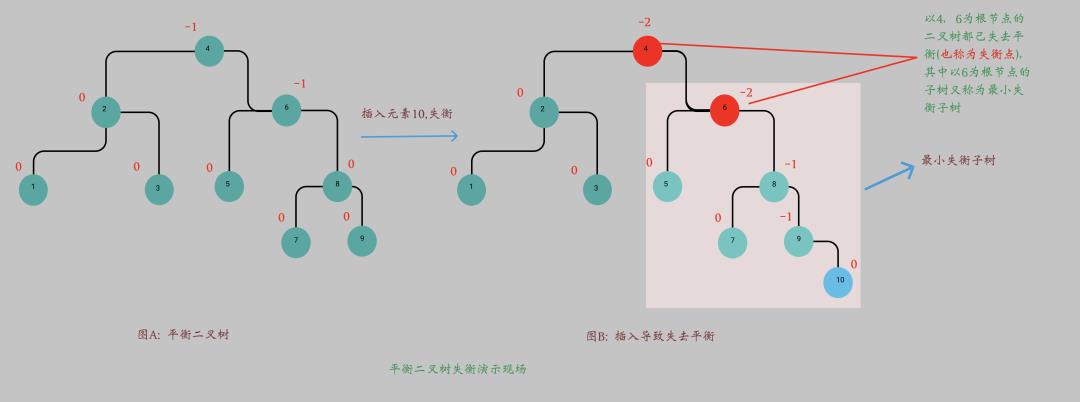
如上图所示, 图A本是一棵平衡二叉树，因插入新元素10导致平衡二叉树失衡变为一棵非平衡二叉树。其中以4，6为根节点的二叉树都失衡。另外我们称呼以6为根节点的二叉树为最小平衡二叉树。

何为最小失衡子树呢？

通常定义为: 在新插入的结点向上查找，以第一个平衡因子的绝对值超过1的结点为根的子树称为最小不平衡子树。 也就是说，一棵失衡的树，是有可能有多棵子树同时失衡的(如上图B的以4，6为根节点的子树)。

失衡后的摊子收拾

平衡二叉树失衡后，该如何调整呢? 如上面所讲，插入节点会导致出现多棵失衡子树。而实际上，我们只需要对最小失衡子树进行旋转调整，使其平衡，则整棵失衡二叉树将再次平衡。

为什么旋转呢?

直观视觉上我们也知道: 哪边的树高，就把那边的树向反方向旋转就可调整高度一致。而旋转的目的就是减少高度，通过降低整棵树的高度来平衡。

怎么旋转呢?

根据旋转的方向，有两种基本处理方式：

• 左旋(右子树高于左子树)
• 右旋(左子树高于右子树)

❝

别忘了，只需要对最小失衡子树进行调整即可。后面我们也将根据这两种基本方式演变出其他方式

左旋

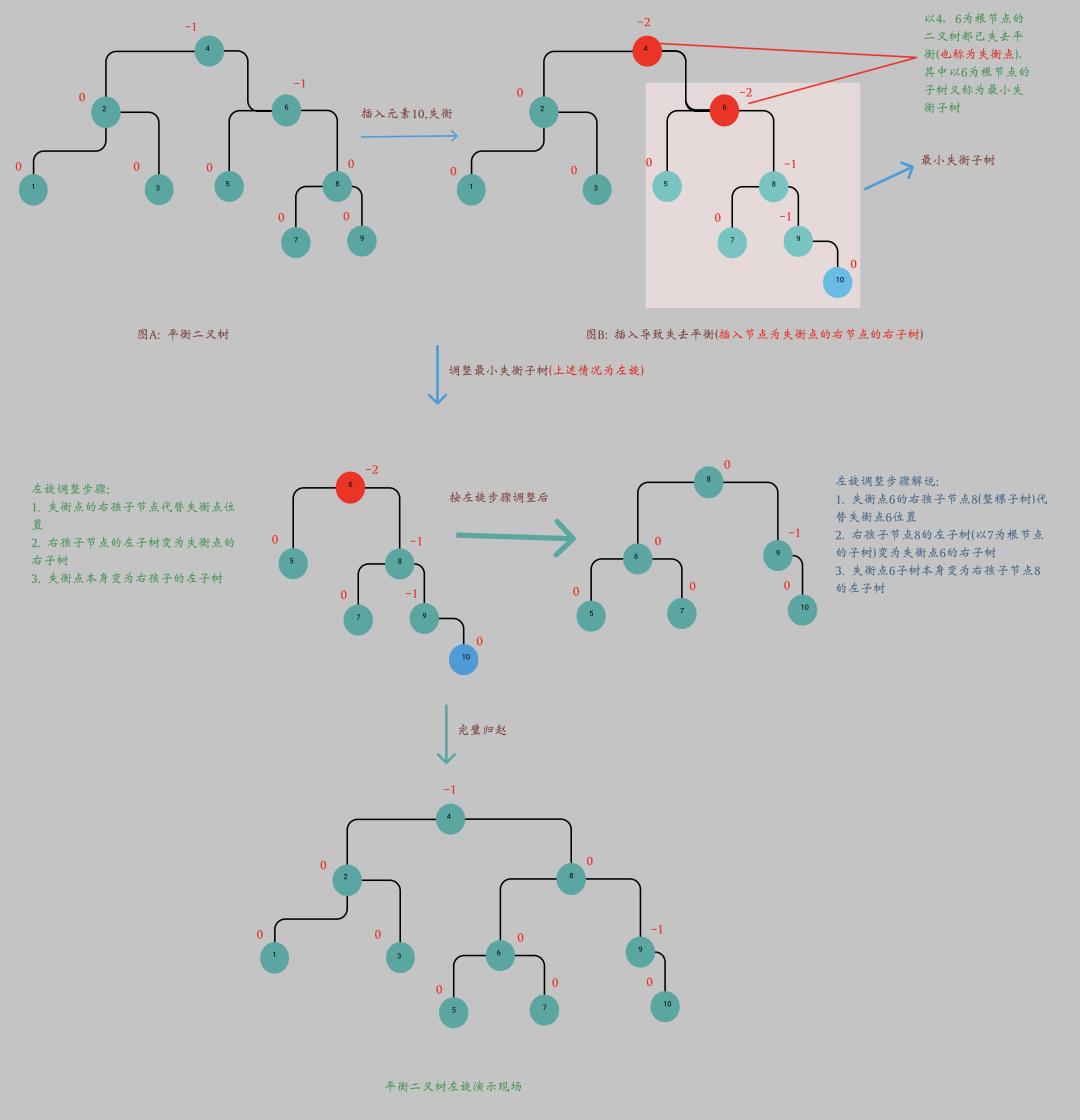
右旋

平衡二叉树结构定义

数据结构定义

type AvlTreeNode struct {
 Value  int // 值
 Height int // 以该节点为根节点, 对应的树的高度, 便于计算平衡因子
 Nums   int // 出现的次数
 Left   *AvlTreeNode
 Right  *AvlTreeNode
}

type AvlTree struct {
 Root *AvlTreeNode //根节点,因不停的调整可能会变化
}

func NewAvlTree() *AvlTree {
 return new(AvlTree)
}

几个常规操作:

func (n *AvlTreeNode) GetHeight() int {
 return n.Height
}

func Max(a int, b int) int {
 if a > b {
  return a
 }
 return b
}

// 获取树的平衡因子
// 左子树高度减去右子树高度
func (n *AvlTreeNode) GetBalanceFactor() int {
 var leftTreeHeight, rigthTreeHeight = 0, 0
 if n.Left != nil {
  leftTreeHeight = n.Left.GetHeight()
 }
 if n.Right != nil {
  rigthTreeHeight = n.Right.GetHeight()
 }
 return leftTreeHeight - rigthTreeHeight
}

// 更新树高度
// 树高=max(左子树高, 右子树高)+1
func (n *AvlTreeNode) UpdateHeight() {
 if n == nil {
  return
 }
 var leftTreeHeight, rigthTreeHeight = 0, 0
 if n.Left != nil {
  leftTreeHeight = n.Left.GetHeight()
 }
 if n.Right != nil {
  rigthTreeHeight = n.Right.GetHeight()
 }
 n.Height = Max(leftTreeHeight, rigthTreeHeight) + 1
 return
}

平衡二叉树的操作

插入操作

添加元素前需要定位到元素的位置，也就是使用二分查找找到该元素需要插入的地方(就是二叉查找树里面的插入操作)。

插入后，需要满足所有节点的平衡因子在 [-1，0，1] 范围内，如果不在，需要进行旋转调整。

❝

也就是说,平衡因子绝对值的最大值即为2，因为平衡因子一旦等于2, 二叉树就需要调整使其平衡

因插入产生的最小失衡子树的根节点我们称为失衡点(前面有讲过哦)。

旋转有四种情况：

• ( RR)在失衡点的右孩子的右子树上插入节点(右子树的左右孩子都行)导致失衡，左旋，转一次。
• ( LL)在失衡点的左孩子的左子树上插入节点(左子树的左右孩子都行)导致失衡，右旋，转一次。
• ( LR)在失衡点的左孩子的右子树上插入节点(右子树的左右孩子都行)导致失衡，先左旋后右旋，转两次。
• ( RL)在失衡点的右孩子的左子树上插入节点(左子树的左右孩子都行)导致失衡，先右旋后左旋，转两次

❝

旋转规律记忆法：单旋(LL、RR)和双旋(LR、RL)，单旋反方向，双旋同方向。

这个听起来很抽象啊, 上图上图...

LL

出现场景:
在失衡点的左孩子的左子树上插入节点 (左子树的左右孩子都行) 导致失衡

解决策略:

• 右旋即可(单旋反方向)

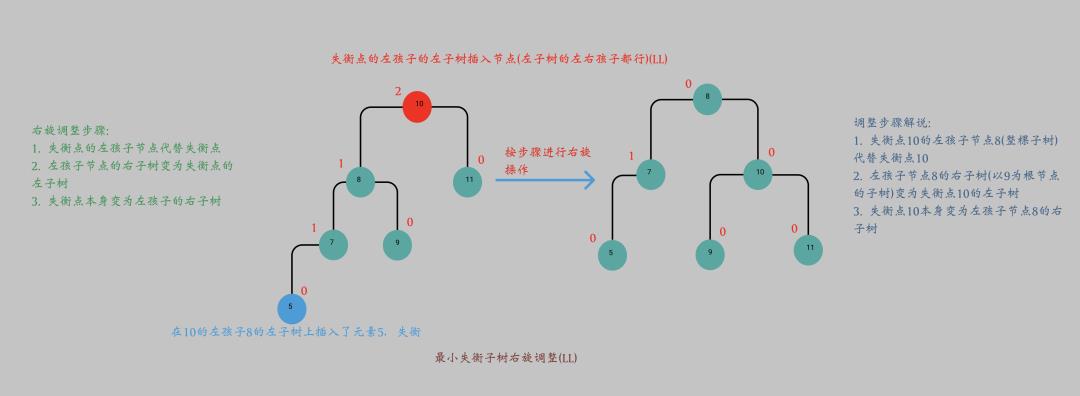
依照上图讲解, 我们很容易写出相关实现:

// 右旋调整步骤:
// 1. 失衡点的左孩子节点代替失衡点
// 2. 左孩子节点的右子树变为失衡点的左子树
// 3. 失衡点本身变为左孩子的右子树
func (n *AvlTreeNode) RigthRotation() *AvlTreeNode {
 newRootNode := n.Left
 n.Left = n.Left.Right
 newRootNode.Right = n
 // 更新失衡点的高度
 n.UpdateHeight()
 // 更新失衡点左孩子节点的高度
 n.Left.UpdateHeight()
 return newRootNode
}

RR

出现场景:
在失衡点的右孩子的右子树上插入节点 (右子树的左右孩子都行) 导致失衡

解决策略:

• 左旋即可(单旋反方向)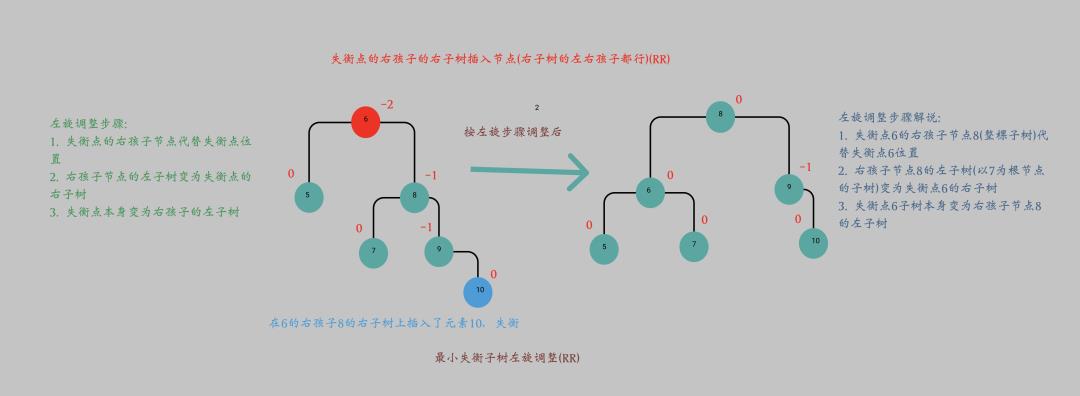
  
  

依照上图讲解, 我们很容易写出相关实现:

// 左旋调整步骤:
// 1. 失衡点的右孩子节点代替失衡点位置
// 2. 右孩子节点的左子树变为失衡点的右子树
// 3. 失衡点本身变为右孩子的左子树
func (n *AvlTreeNode) LeftRotation() *AvlTreeNode {
 newRootNode := n.Right
 n.Right = n.Right.Left
 newRootNode.Left = n
 // 更新失衡点的高度
 n.UpdateHeight()
 // 更新失衡点右孩子节点的高度
 n.Right.UpdateHeight()
 return newRootNode
}

LR

出现场景:
在失衡点的左孩子的右子树上插入节点 (右子树的左右孩子都行) 导致失衡

解决策略:

• 先左旋后右旋即可(双旋同方向)
• 具体步骤都在图里面...

依照上图讲解, 我们很容易写出相关实现:

// 左旋然后右旋
// 调整策略:
// 1. 先绕失衡点的左孩子节点左旋做局部调整
// 2. 再绕失衡点右旋即可完成整体调整
func (n *AvlTreeNode) LeftRightRotation() *AvlTreeNode {
 n.Left = n.Left.LeftRotation()
 return n.RigthRotation()
}

RL

出现场景:
在失衡点的右孩子的左子树上插入节点 (左子树的左右孩子都行) 导致失衡

解决策略:

• 先右旋后左旋即可(双旋同方向)
• 具体步骤都在图里面...
  
  

依照上图讲解, 我们很容易写出相关实现:

// 右旋然后左旋
// 调整策略:
// 1. 先绕失衡点的右孩子节点右旋做局部调整
// 2. 再绕失衡点左旋即可完成整体调整
func (n *AvlTreeNode) RightLeftRotation() *AvlTreeNode {
 n.Right = n.Right.RigthRotation()
 return n.LeftRotation()
}

完整插入代码

基于上述的拆分出来四种场景,那么相关的插入代码也就水到渠成了。如下示:

func (tree *AvlTree) Insert(value int) {
 // 因插入新的元素,可能造成树失衡调整,而使根节点变更
 tree.Root = tree.Root.Insert(value)
 return
}

// 处理节点树高度问题
func (n *AvlTreeNode) HandleBF(value int) *AvlTreeNode {
 // 平衡因子(左子树和右子树高度之差)
 factor := n.GetBalanceFactor()
 newNode := new(AvlTreeNode)
 // 左子树的高度变高了，导致左子树-右子树的高度从1变成了2。
 if factor == 2 {
  if value < n.Left.Value {
   // 表示在左子树上插上左儿子导致失衡，需要单右旋：
   newNode = n.RigthRotation()
  } else {
   //表示在左子树上插上右儿子导致失衡，先左后右旋：
   newNode = n.LeftRightRotation()
  }
 } else if factor == -2 { // 右子树的高度变高了，导致左子树-右子树的高度从-1变成了-2。
  if value > n.Right.Value {
   // 表示在右子树上插上右儿子导致失衡，需要单左旋：
   newNode = n.LeftRotation()
  } else {
   //表示在右子树上插上左儿子导致失衡，先由后左旋：
   newNode = n.RightLeftRotation()
  }
 } else {
  newNode = n
 }
 return newNode
}

func (n *AvlTreeNode) Insert(value int) *AvlTreeNode {
 if n == nil {
  return &AvlTreeNode{Height: 1, Nums: 1, Value: value}
 }
 // 插入的值小于节点值，要从左子树继续插入
 if value < n.Value {
  n.Left = n.Left.Insert(value)
  n = n.HandleBF(value)
  // 插入的值大于节点值，要从右子树继续插入
 } else if value > n.Value {
  n.Right = n.Right.Insert(value)
  n = n.HandleBF(value)
  // 插入值相同,重复次数加1即可
 } else {
  n.Nums += 1
 }
 // 刷新新树根高度
 n.UpdateHeight()
 return n
}

查询操作

相关的查询包括查询指定值、最小值、最大值等，相关操作跟前文所讲的二叉查找树是通用的,因此这里我们就直接给出相关实现,不再做相关讲解。

// 二叉查找树的搜索
func (tree *AvlTree) Search(value int) *AvlTreeNode {
 if tree.Root == nil {
  return nil
 }
 currentNode := tree.Root
 for currentNode != nil {
  // 小于子树根节点的值
  if value < currentNode.Value {
   currentNode = currentNode.Left
   // 大于子树根节点的值
  } else if value > currentNode.Value {
   currentNode = currentNode.Right
   // 找到该值
  } else {
   return currentNode
  }
 }
 return nil
}

// 查询最小值
func (tree *AvlTree) FindMin() *AvlTreeNode {
 if tree.Root == nil {
  return nil
 }
 currentNode := tree.Root
 // 一直往左子树遍历
 for currentNode != nil {
  if currentNode.Left != nil {
   currentNode = currentNode.Left
  } else {
   break
  }
 }
 return currentNode
}

// 查询最大值
func (tree *AvlTree) FindMax() *AvlTreeNode {
 if tree.Root == nil {
  return nil
 }
 currentNode := tree.Root
 // 一直往右子树遍历
 for currentNode != nil {
  if currentNode.Right != nil {
   currentNode = currentNode.Right
  } else {
   break
  }
 }
 return currentNode
}

删除操作

平衡二叉树的删除操作跟二叉查找树比较类似，也是分情况讨论，平衡二叉树主要就是在删除后，需要做相关的失衡调整操作。

删除元素有三大种情况：

• 如果被删除结点A有两个子结点， 将该结点右子树内的最小结点取代A, 并删除最小节点。
• 如果被删除结点A只有一个子结点( 左孩子或者右孩子)，就直接将A的子结点连至A的父结点上，并将A删除( 根据平衡二叉树的定义, 一个节点只有一个子节点的时候，该子节点比为该节点的孩子节点,否则就失衡)
• 删除的节点是叶子节点，没有儿子，直接删除后看离它最近的父亲节点是否失衡，做调整操作。

根据上述的步骤描述,我们也很容易写出相关的代码实现,如下所示:

/*删除元素
1. 如果被删除结点A有两个子结点，将该结点右子树内的最小结点取代A, 并删除最小节点。
2. 如果被删除结点A只有一个子结点(左孩子或者右孩子)，就直接将A的子结点连至A的父结点上，并将A删除(根据平衡二叉树的定义, 一个节点只有一个子节点的时候，该子节点比为该节点的孩子节点,否则就失衡)
3. 删除的节点是叶子节点，没有儿子，直接删除后看离它最近的父亲节点是否失衡，做调整操作。
*/
func (n *AvlTreeNode) Delete(value int) *AvlTreeNode {
 if n == nil {
  return nil
 }
 if value < n.Value {
  // 从左子树开始删除
  n.Left = n.Left.Delete(value)
 } else if value > n.Value {
  // 从右子树开始删除
  n.Right = n.Right.Delete(value)
 } else {
  // 找到待删除的节点
  if n.Left != nil && n.Right != nil {
   // 有两个节点
   // 步骤1: 找到右孩子的最小值替换该待删除节点
   rightMinNode := n.Right.FindMin()
   n.Value = rightMinNode.Value
   n.Nums = rightMinNode.Nums
   // 步骤2: 删除右孩子的最小值
   n.Right = n.Right.Delete(n.Value)
  } else if n.Left != nil {
   // 只有左孩子
   n = n.Left
  } else if n.Right != nil {
   // 只有右孩子
   n = n.Right
  } else {
   // 左右孩子均无,为叶子节点
   n = nil
   return n
  }
 }
 // 调整高度
 n.UpdateHeight()
 return n
}

完整代码实现

完整代码实现:https://github.com/yiye93/algo

^^代码不易，希望大家给个星鼓励下^^

下面放一波链接, 本人会持续在上面更新.....

link

• 公众号: 程序员的进击之路
• github: https://github.com/yiye93/algo