Mathematica软件教程：函数式编程

Posted 2021-04-09 天演融智

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Mathematica软件教程：函数式编程相关的知识，希望对你有一定的参考价值。

【前言】

作为Mathematica的开发商，Wolfram公司近几年致力于将其作为一门编程语言进行推广(这也是Wolfram公司改称Mathematica为Wolfram Language的原因，本文仍沿用旧称)。如今也已经有了不少优秀的介绍Mathematica编程的书籍，例如《Power Programming with Mathematica》、《Mathematica Programming: An Advanced Introduction》、《An Elementary Introduction to the Wolfram Language》。尽管如此，但按照笔者经验，对于不少人来说，Mathematica还是很难上手，其独特的编程风格仍然很难适应。

由于使用方法不当(甚至是道听途说)造成了一个广泛的误解：“Mathematica就是一个高级计算器，推推公式什么的还可以，遇到实际问题就不行了。”笔者回顾自己自学Mathematica的经历，也走过不少弯路，期间也不乏有如上那样的误解。作为“过来人”，笔者也对一些人在学习Mathematica过程中遇到的瓶颈也深有体会。本文就是从一个“过来人”的角度谈谈对Mathematica中函数式编程的理解。

笔者认为有些不恰当的前概念会阻碍Mathematica的学习。数学上认识的局限性，甚至是一些其他编程语言的“经验”，都有可能是阻碍学习Mathematica的症结所在。而对这些非技术方面的“意识”角度的探讨，现阶段的资料中还比较缺乏。原因之一也许是内容比较“虚”，不易做到“言之有物”。

笔者认为探讨这些“虚”的问题，还是通过举例子的方式为好。本文的主线不是解决某个具体的编程问题，而是围绕一些笔者认为重要的观念进行举例阐释，体现出Mathematica的精妙设计之处，希望能对读者有所启发。限于水平，对这些意识层面的探讨难免主观，也不可能面面俱到，本文权作引玉之砖。

【正文】

如Mathematica的名字本身所暗示的那样，Mathematica的内部函数在设计的时候就带有一种浓厚的“数学味”，使其在设计的时候远超“能用就行”的，具有数学家一样的认识深度和战略眼光。

例如，学过线性代数的人知道，对一组向量可以通过Gram-Schmidt正交化的步骤，把原本非正交的基底变为正交的基底，这其中需要不断地求投影。如果不知道Mathematica自带Orthogonalize这个函数也不要紧，可以自己用Projection模拟这个正交化过程，思路非常简单直接。例如这么写(摘自帮助文档，有改动)：

gs[vecs_] := Module[{ovecs = vecs},

Do[ovecs[[i]] -= Projection[ovecs[[i]], ovecs[[j]]], {i, 2, Length[vecs]}, {j, 1, i - 1}];

ovecs]

对于长的“像向量”的东西，例如数值的列表，这个确实运行得很好。例如可以通过下面的代码验证正交性：

b = gs[RandomReal[1, {3, 3}]]

Chop@Outer[Dot, b, b, 1]

Mathematica给出：

{{0.387954, 0.0396196, 0.222666}, {0.0400743, 0.434263, -0.147091}, {-0.302278, 0.194557, 0.492044}}和{{0.201658, 0, 0}, {0, 0.211826, 0}, {0, 0, 0.371332}}.

最后的矩阵确实是对角的，因此程序正确！

向量的广泛一个认识是，它是有大小有方向的“东西”，这个“东西”在计算机中最自然和直接的表示方式是列表，在Mathematica中用一对大括号“{}”括起来。尽管笔者也不怀疑，这个程序对于大多数情况是够用了。可如果对向量的认识仅限于一个个具体的列表，则未免让众多数学家们摇头感叹。

数学上的向量远超这种直观的理解，只要满足线性运算的八条规则的“东西”，都能叫做向量。定义了内积之后，这些向量之间就可以谈及正不正交。可没说向量就是由数字组成的列表。

如果读者仔细阅读Mathematica的Projection的使用说明，会发现一个可以额外定义内积的第三个参数f：

Projection[u,v,f] finds projections with respect to the inner product function f.

这里f可以定义两个“向量”怎么做内积。有了这个之后我们可以跳出“列表”向量的窠臼，得到所谓的“正交多项式”：

gs[vecs_, ip___] := Module[{ovecs = vecs},
Do[ovecs[[i]] -= Projection[ovecs[[i]], ovecs[[j]], ip], {i, 2,
Length[vecs]}, {j, 1, i - 1}];
ovecs]
gs[{1, x, x^2, x^3}, Integrate[#1 #2, {x, -1, 1}] &]

运行结果为：

{1, x, -(1/3) + x^2, -((3 x)/5) + x^3}

除了整体的常数因子之外，这就是勒让德多项式(Legendre Polynomials)！

当然，Mathematica可以直接用Orthogonalize完成同样的事情：

Orthogonalize[{1, x, x^2, x^3}, Integrate[#1 #2, {x, -1, 1}] &]

居然还有如此简单的得到正交多项式的方法，不知读者是否感到惊叹呢？而一旦掌握了相关的数学知识，这种方法也并不神秘，只不过是真实地还原了数学的定义而已：向量可以是列表但不局限于列表，只要某个东西符合向量的“操作定义”它就可以称之为向量。

Mathematica中也有类似的哲学，函数可以对很自然地对某种类型的数据起作用，比如列表，但又有超出这种类型的时候。这种函数(数学上的映射)和实际数据(自变量)相互独立，也是函数式编程的一个特点。Orthogonalize就是一个比较典型的例子。

除了体现编程中把一个函数的功能做专一且做到极致以外，如果没有一定的数学功底，意识不到数学上还有类似把多项式“正交化”这样的操作，则无论有多么高超的编程技巧也无法写出如此强大的函数。而一旦有这层意识，就会觉得这么设计是很自然的：函数就该有这个功能才对！

从其他编程语言转学Mathematica需要注意这种意识上的壁垒，有意识地反思是不是过于为机器或程序着想，抛弃一些照顾底层语言的习惯，跳出程序能用就行的实用主义，多查帮助文档，尤其是其中的Details、Backgrounds、Generalizations & Extensions部分，有很多值得学习和思考的地方。否则虽然会用Mathematica编程，但无法掌握其精髓。当然，像笔者被Mathematica“惯坏”了之后，学其他编程语言往往会觉得碍手碍脚。

对用户来说，自然不想分别对整数、实数和复数都定义一套同样的运算，在其他编程语言中往往需要通过函数的重载机制来实现，而Mathematica中就不用理会这些细节。

举一个看起来平庸实际不平庸的例子：加法运算。

就如同数学上的定义那样，Mathematica中可以对整数、实数和复数进行直观的加法运算；除此以外，如果对两个“结构相同”的列表：

{a, b, {1.2}} + {3.14, x, {2.1}}

进行求和，Mathematica会自动将“对应的元素”求和，而得到：

{3.14 + a, b + x, {3.3}}.

用Mathematica的术语来说，加法被自动Thread(逐项作用)了，这个功能对批量操作大量的数据提供了方便。

例如，如果需要对一个数组lst的每个元素增加2.5，则可以直观地写：lst+2.5，而不需要用循环遍历每个元素重复同样的操作。这样除了减小代码量，也提高程序运行效率，除此以外，笔者更想强调的是Mathematica可以这么做的背后的风格和哲学：

只要两个(或多个)“东西”有着符合直觉的加法操作，这个操作就应该能进行下去，而不管这个“东西”究竟是什么。

这极大地拓展了Mathematica的灵活性和通用性，也常常让Mathematica的程序惊艳众人。毫不夸张地说说这套哲学统领了Mathematica的设计，用Wolfram公司的话总结为：“在Mathematica中，一切都是表达式”。

正如抽象代数中，研究的重点是对象的操作，而非对象本身。作为一个类比，学习Mathematica也要有如此的抽象能力：不要沦为程序的奴隶，多提炼程序背后的逻辑，这样读Mathematica程序才会高屋建瓴之感。

Mathematica中，体现这种抽象的另一个例子是所谓的纯函数(pure function)。纯函数经常会和Map，Apply等函数联合起来，因此往往会见到如下这样的程序(Steven Wolfram的Simple Phone Dialer)：

Manipulate[
Grid[Partition[
   MapIndexed[
    Button[First[#2] /. {10 -> "*", 11 -> 0, 12 -> "#"},
      EmitSound[Play[Total[Sin[2 Pi # t] & /@ #], {t, 0, len}]],
      ImageSize -> {40, 40}] &,
    Flatten[Outer[List, {697, 770, 852, 941}, {1209, 1336, 1477}],
     1]], 3]], {{len, 0.1, "duration"}, 0.01, 1}]

对有些人，这如同天书一般难以理解，毕竟#&/@这些确实像屏蔽不文明用语的占位符(所谓的grawlix)。

正如前面强调的，对一段程序而言，有时候函数参数的具体形式往往不那么重要，因此我们才将精力花在理解函数本身上去。数学上，为了方便使用，不同的函数总要有不同的名字，以作表示和区分。程序中也往往也是如此，因此我们可以看到蔚为壮观的程序包使用手册(例如Mathematica的帮助文档)。

函数名字固然很重要，但是有时候为某个函数起名字反而是个不小的麻烦。首先需要注意避免和其他的函数名冲突，其次要体现函数的特点便于理解和记忆，这并不容易做到。如果某个函数仅用一次，起名字这个步骤就显得多余。

随着对函数理解的不断深入，我们可以进一步发现，实际上函数的名字只是一个代号，代号本身也不重要，只要能用某种方式表达函数做了什么即可。Mathematica中我们能抛开这个代号，直达函数的映射本质，这就是所谓的纯函数。

举例来说，如果定义一个函数“mySinSquare”，它对自变量先求正弦值，然后平方。一般地我们可以用如下的方式定义：

mySinSquare [x_]:=Sin[x]^2

如果对一个列表批量进行这样的操作，可以这样：

mySinSquare/@RandomReal[{},5]

(实际上最简单的是利用Mathematica自动Thread的特性：Sin[RandomReal[{},5]]^2.)

也可以用纯函数的方式这么定义：

Function[x,Sin[x]^2] /@RandomReal[{},5]

你也许会说这个做法并没有简单多少，因为我还是需要一个形式参数x，能不能连x都不需要呢？当然可以，也应该这样！

实际上Function[x,Sin[x]^2]可以简化为：Sin[#]^2&(注意其中的&符号必不可少，它代表一个纯函数的完结)。Mathematica中的#1、#2、#n分别代表第一个、第二个、第n个参数……有了这个占位符之后，我们可以放开手脚直接，通过与一些函数选项的精心搭配，可以极大地提高代码可读性。

例如，如果需要在 sin(x y) 的三维图像中，标记其与参数方程的交线。一般的思路是求解交线的参数方程然后作图。对于如上的简单问题不难得到交线的参数方程为：

然后用ParametricPlot3D和Plot3D画图即可。

对于简单的函数尚能如此，但是复杂的函数就很难这么进行下去了，实际上我们可以用Plot3D的MeshFunctions选项，很方便地进行：

Plot3D[Sin[x y], {x, -3, 3}, {y, -3, 3},
MeshFunctions -> {#1^2 + #2^2 &},
Mesh -> {{2}},
MeshStyle -> {Red, Thick},
PlotStyle -> Opacity[0.5]
]
按照Plot3D的约定，#1、#2分别代表横纵坐标，所以代码中的“#1^2 + #2^2 &”就是函数的纯函数写法。

上面代码的运行结果为：

除了从上面的例子学习纯函数的使用之外，我们也应该学会用另一种眼光看待函数作图：如果已经有了 sin9(xy)的三维图形，则交线属于对这个图像的附加修饰，这些附加修饰不应该重新计算，而应该充分利用已有的图形和相关的操作机制进行合理地变换，从而达到目的。

非常幸运的是Mathematica提供了这些变换如MeshFunctions.

如果对上面的图像的颜色不满意，需要按照将根据不同的高度(即的值)染上不同的颜色以便区分。我们需要的仅仅是构造一个颜色函数，例如根据函数值用彩虹色渐变，Mathematica应该提供一种机制方便将此函数作用到这个图形上去，具体怎么作用，我们不想关心。这就是典型的函数式思维：关注点在于要做什么，而不是如何做。Mathematica的确没让我们失望，ColorFunction正是我们需要的：

Plot3D[Sin[x y], {x, -3, 3}, {y, -3, 3},

MeshFunctions -> {#1^2 + #2^2 &},

Mesh -> {{2}},

MeshStyle -> {Red, Thick},

PlotStyle -> Opacity[0.8],

ColorFunction -> ColorData["Rainbow"]]

返回的图形是:

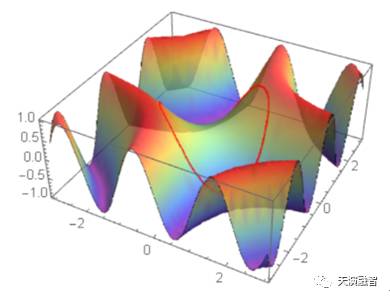
Mathematica软件教程：函数式编程