K-Means聚类算法与Python实现

Posted 2021-04-09 机器学习与量化投资

在数据挖掘中，K-Means算法从一个目标集中创建多个组，每个组的成员都是比较相似的。这是个想要探索一个数据集时比较流行的聚类分析技术,也可以说是一种最简单的聚类算法了。

算法实现过程：

k-means 算法的工作过程说明如下：

首先从含n个数据对象的数据集中任意选择k个对象作为初始聚类中心；

对于所剩下其它对象，则根据它们与这些聚类中心的相似度，分别将它们分配给与其最相似的（聚类中心所代表的）聚类；

然后再计算每个所获新聚类的聚类中心（该聚类中所有对象的均值）；

不断重复这一过程直到标准测度函数开始收敛为止。

一般都采用均方差作为标准测度函数。

k个聚类有以下特点：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。

伪代码说明表示流程如下：

选择k个点作为起始质心(一般随机选择) 当任意一个点的簇分配结果发生改变时 对数据集中的每个数据点 对每个质心 计算质心与数据点之间的距离 将数据点分配到距其最近的簇 对每一个簇，计算簇中所有点的均值并将均值作为质心

算法优缺点：

优点：容易实现，最大好处就是这个了

缺点：

1）k值的选择是用户指定的，不同的k得到的结果会有挺大的不同

2）对k个初始质心的选择比较敏感，容易陷入局部最小值

3）存在局限性，非球状数据分布可能就搞不定了

4）数据较大时，效率较低，收敛速度慢

算法实现和设计：

代码实现如下

import numpy as np import random import codecs import re import matplotlib.pyplot as plt # 计算欧氏距离 def calculate_distance(vec1, vec2): return np.sqrt(np.sum(np.square(vec1 - vec2))) # 载入数据测试数据集 def load_data_set(input_file): input_date = codecs.open(input_file, 'r', 'utf-8').readlines() data_set = list() for line in input_date: line = line.strip() strList = re.split('[ ]+', line) # 去除多余的空格        numList = list() for item in strList: num = float(item) numList.append(num) data_set.append(numList) return data_set # data_set = [[], [], [], ...] # 初始化k个质心，随机获取 def init_centroids(data_set, k): return random.sample(data_set, k) # 对每个属于data_set的item，计算item与centroid_list中k个质心的欧式距离，找出距离最小的 # 并将item加入相应的簇类中 def min_distance(data_set, centroid_list): cluster_dict = dict() # 用dict来保存簇类结果    for item in data_set: vec1 = np.array(item) # 转换成array形式        flag = 0  # 簇分类标记，记录与相应簇距离最近的那个簇        min_dis = float("inf") # 初始化为最大值        for i in range(len(centroid_list)): vec2 = np.array(centroid_list[i]) distance = calculate_distance(vec1, vec2) # 计算相应的欧式距离            if distance < min_dis: min_dis = distance flag = i # 循环结束时，flag保存的是与当前item距离最近的那个簇标记        if flag not in cluster_dict.keys(): # 簇标记不存在，进行初始化            cluster_dict[flag] = list() cluster_dict[flag].append(item) # 加入相应的类别中    return cluster_dict # 返回新的聚类结果 def get_centroids(cluster_dict): # 得到k个质心    centroid_list = list() for cluster_key in cluster_dict.keys(): # 计算每列的均值，找到质心        centroid = np.mean(np.array(cluster_dict[cluster_key]), axis=0) centroid_list.append(centroid) return np.array(centroid_list).tolist() # 计算簇集合间的均方误差 # 将簇类中各个向量与质心的距离进行累加求和 def get_var(cluster_dict, centroid_list): sum = 0.0    for cluster_key in cluster_dict.keys(): vec1 = np.array(centroid_list[cluster_key]) distance = 0.0        for item in cluster_dict[cluster_key]: vec2 = np.array(item) distance += calculate_distance(vec1, vec2) sum += distance return sum # 展示聚类结果 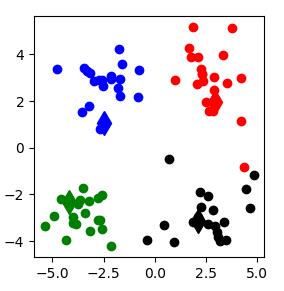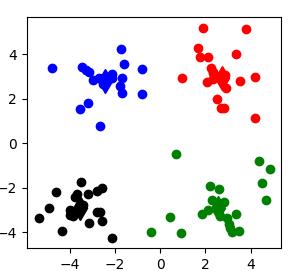def show_cluster(centroid_list, cluster_dict): # 不同簇类的标记 'or' --> 'o'代表圆，'r'代表red，'b':blue    color_mark = ['or', 'ob', 'og', 'ok', 'oy', 'ow'] # 质心标记 同上'd'代表棱形    centroid_mark = ['dr', 'db', 'dg', 'dk', 'dy', 'dw'] for key in cluster_dict.keys(): # 画质心点        plt.plot(centroid_list[key][0], centroid_list[key][1], centroid_mark[key], markersize=12) for item in cluster_dict[key]: # 画簇类下的点            plt.plot(item[0], item[1], color_mark[key]) plt.show() if __name__ == '__main__': input_file = "testData.txt"    dataSet = load_data_set(input_file) # 初始化质心，设置k=4    centroidList = init_centroids(dataSet, 4) # 第一次聚类迭代    clusterDict = min_distance(dataSet, centroidList) # 获得均方误差值，通过新旧均方误差来获得迭代终止条件    newVar = get_var(clusterDict, centroidList) oldVar = -0.0001  # 旧均方误差值初始化    print('***** 第1次迭代 *****') print('簇类') for key in clusterDict.keys(): print(key, ' --> ', clusterDict[key]) print('k个均值向量: ', centroidList) print('平均均方误差: ', newVar) show_cluster(centroidList, clusterDict) # 展示聚类结果    k = 2    while abs(newVar - oldVar) >= 0.0001: # 当连续两次聚类结果小于0.0001时，迭代结束        centroidList = get_centroids(clusterDict) # 获得新的质心        clusterDict = min_distance(dataSet, centroidList) # 新的聚类结果        oldVar = newVar newVar = get_var(clusterDict, centroidList) print('***** 第%d次迭代 *****' % k) print('簇类') for key in clusterDict.keys(): print(key, ' --> ', clusterDict[key]) print('k个均值向量: ', centroidList) print('平均均方误差: ', newVar) show_cluster(centroidList, clusterDict) # 展示聚类结果        k += 1

运行效果截图：(每次结果可能存在不同)

1.

2：

3：

4：

5：

对于如何提高聚类效果，这就是另一个话题啦，我们后面再讨论。