常用数据挖掘算法从入门到精通 第三章 K-中心点聚类算法

Posted 2021-04-09 小AI咨询

今天主要讲述K-中心点聚类算法，并附有详细的案例来帮助大家理解。K-中心点聚类算法也称K-medoids聚类算法。

K-中心点聚类算法简介

第二章中讲了K-means聚类算法，但是K-means聚类算法最大的一个缺点就是对于离群点是敏感的，一个具有很大的极端值的数据对象可能会显著地扭曲数据的分布。采用误差平方和准则函数作为聚类性能评价准则更是严重恶化了这一影响。为了降低这种敏感性，可以不采用簇中对象的均值最为参照点，而是在每个簇中选出一个实际的对象来代表该簇。其余的每个对象聚类到与其最相似的代表性对象所在的簇中。这样的划分方法仍然是基于最小化所有对象与其对应的参照点之间的相异度之和的原则来执行。通常，该算法重复迭代，直到每个代表对象都成为它的簇的实际中心点，或是最靠中心的对象。这种算法称为K-中心点聚类算法。

对于K-中心点聚类，首先随意选择初始代表对象/种子，只要能够提高聚类质量，迭代过程就继续用非代表对象替换代表对象。聚类结果的质量用代价函数来评估，该函数量度对象与其簇的代表对象之间总的相异度。

K-中心点聚类算法原理

K-中心点聚类算法选用簇中位置最中心的对象作为代表对象，试图对n个对象给出k个划分。

• 代表对象也被称为是中心点，其他对象则被称为非代表对象。

• 最初随机选择K个对象作为中心点，该算法反复地用非代表对象来代替代表对象，试图找出更好的中心点，以改进聚类的质量。

• 在每次迭代中，所有可能的对象对被分析，每个对中的一个对象是中心点，而另一个是非代表对象。

• 对可能的各种组合，估算聚类结果的质量。一个对象Oi被可以产生误差平方总和减少的对象代替。在一次迭代中产生的最佳对象集合成为下次迭代的中心点。

• 为判定一个非代表对象Oh是否是当前一个代表对象Oi的好的替代，对每一个非中心点对象Oj，下面的四种情况被考虑：

• 第一种情况：Oj当前隶属于中心点对象Oi。如果Oi被Oh所代替作为中心点，且Oj离某个中心点Om最近，i≠m，那么Oj被重新分配给Om。

• 第二种情况：Oj当前隶属于中心点对象Oi。如果Oi被Oh所代替作为中心点，且Oj离Oh最近，那么Oj被重新分配给Oh。

• 第三种情况：Oj当前隶属于中心点Om，m≠i。如果Oi被Oh代替作为中心点，而Oj依然离Om最近，那么对象的隶属不发生变化。

• 第四种情况：Oj当前隶属于中心点Om，m≠i。如果Oi被Oh代替作为一个中心点，且Oj离Oh最近，那么Oi被重新分配给Oh。

• 每当重新分配发生时，误差平方和E所产生的差别对代价函数有影响。因此，如果一个当前的中心点对象被非中心点对象所代替，代价函数表征误差平方和所产生的差别。替换的总代价是所有非中心点对象所产生的代价之和。

• 如果总代价是负的，那么实际的误差平方和将会减小，Oi可以被Oh替代。

• 如果总代价是正的，则当前的中心点Oi被认为是可接受的，在本次迭代中没有变化。

• 总代价定义如下：

总代价

其中，Cjih表示Oj在Oi被Oh代替后产生的代价。

四种情况的代价函数

下面我们将介绍上面所述的四种情况中代价函数的计算公式，其中所引用的符号有：Oi和Om是两个原中心点，Oh将替换Oi作为新的中心点。其中相异度或距离函数d的选择因数据类型不同而可以有不同的选择，对于K-中心点聚类算法一般选择曼哈顿距离，具体的计算公式可以参考同系列文章《常用数据挖掘算法从入门到精通 第二章 K-means聚类算法》中有关于相似度或者距离评价准则计算的详细介绍和计算公式。

代价函数计算公式

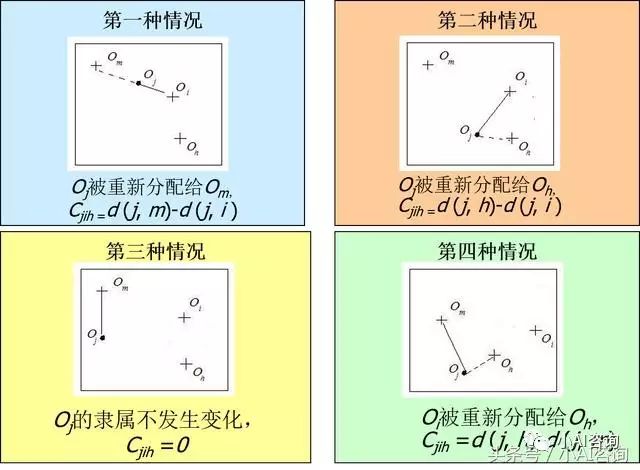
代价函数计算图示

K-中心点聚类算法步骤

算法 K-中心点算法

输入：簇的数目K和包含n个对象的数据库。

输出：K个簇，使得所有对象与其最近中心点的相异度总和最小。

（1） 任意选择K个对象作为初始的簇中心点；

（2） REPEAT

（3） 指派每个剩余的对象给离它最近的中心点所代表的簇；

（4） REPEAT

（5） 选择一个未被选择的中心点Oi；

（6） REPEAT

（7） 选择一个未被选择过的非中心点对象Oh；

（8） 计算用Oh代替Oi的总代价并记录在S中；

（9） UNTIL 所有的非中心点都被选择过；

（10） UNTIL 所有的中心点都被选择过；

（11） IF 在S中的所有非中心点代替所有中心点后计算出的总代价有小于0存在 THEN 找出S中的用非中心点替代中心点后代价最小的一个，并用该非中心点替代对应的中心点，形成一个新的K个中心点的集合；

（12）UNTIL 没有再发生簇的重新分配，即所有的S都大于0.

K-中心点聚类算法实例

假如空间中的五个点｛A、Ｂ、Ｃ、Ｄ、Ｅ｝如下图所示，各点之间的距离关系如下表所示，根据所给的数据对其运行K-中心点聚类算法实现划分聚类（设K=2）。

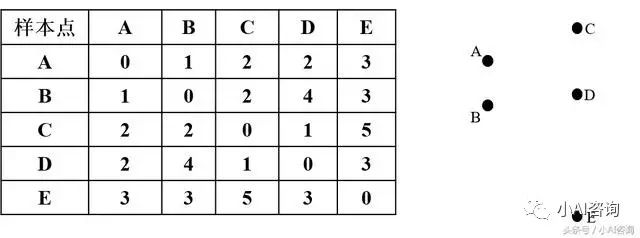
初始样本点和样本点间距离表

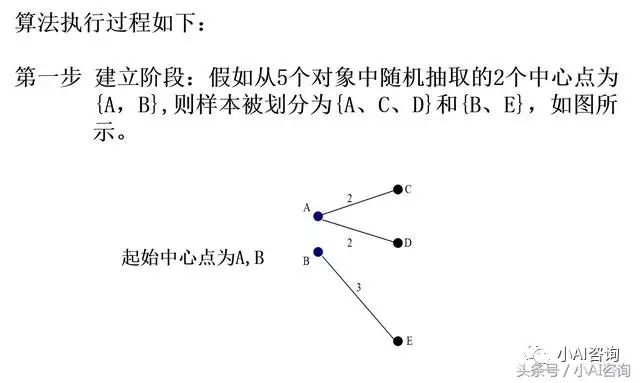
第一步

第二步

总代价计算

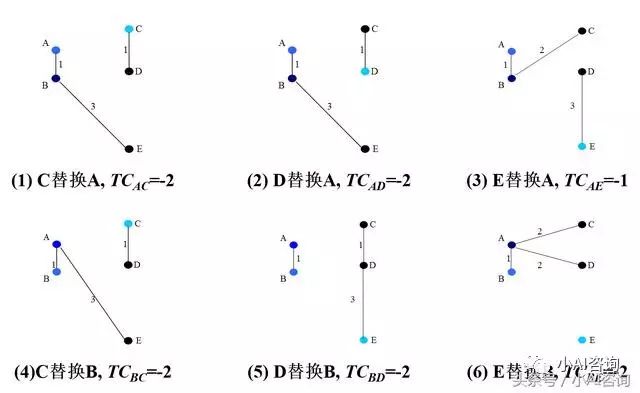
总代价计算结果图示

第一次迭代结果