精彩文章推荐广西大学 覃华等:基于概率无向图模型的近邻传播聚类算法
Posted 控制与决策
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了精彩文章推荐广西大学 覃华等:基于概率无向图模型的近邻传播聚类算法相关的知识,希望对你有一定的参考价值。
本文引用信息
覃华, 詹娟娟, 苏一丹. 基于概率无向图模型的近邻传播聚类算法[J]. 控制与决策, 2017, 32(10): 1796-1802.
QIN Hua, ZHAN Juanjuan, SU Yidan. Affinity propagation clustering algorithm based on probabilistic undirected graphical model[J]. Control and Decision, 2017, 32(10): 1796-1802.
DOI: 10.13195/j.kzyjc.2016.0861
基于概率无向图模型的近邻传播聚类算法
覃华, 詹娟娟, 苏一丹
1研究背景
近邻传播聚类算法(AP)是一种新型聚类算法,和传统的K-means等聚类算法相比,其优点是事先不需要知道数据的簇个数,然后运用它的信息处理机制从数据中筛选出簇中心,将与簇中心相似的数据划分到同一簇中,从而将数据集自动划分为若干个类别。AP是为数不多的自动聚类算法之一,在各领域中有广泛的应用前景。
AP聚类算法最特别的特点是保证了数据集中每个样本点均可通过公平竞争成为候选聚类中心点,即在计算之初,每个数据点成为簇中心的概率均被视为一致。但在现实的计算过程中,如果将每个数据点的竞争初始能力同等化,将导致那些竞争力低下的样本数据点拖延计算时间、增加计算时耗,甚至影响最终的聚类结果。由图1所示的数据分布特征可知,Xi比Xj成为聚类中心的概率更大,故将每个数据点成为簇中心点的概率视为一致,会导致AP算法花费更多的迭代次数、计算时间和计算时耗去发现真正的聚类中心。因此,如何提高AP算法的计算效率和聚类精度是一个值得研究的问题。
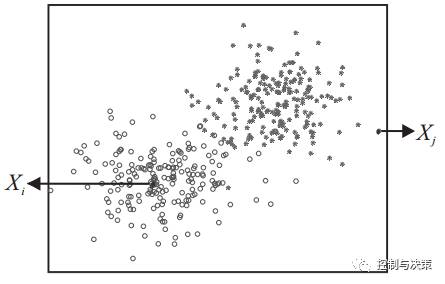
图 1 数据样本分布图
2技术路线
在AP聚类前,如果能预测出各数据样本成为簇中心的概率,显然能帮助AP算法提高计算效率和聚类精度,本论文提出使用概率无向图模型来估算各数据成为簇中心的概率。为方便描述,假定有一个数据集X={x1,x2,x3,x4},X中有4个数据样本,用概率无向图模型估算这4个数据样本成为簇中心的概率,所用方法描述如下。
1) 首先,计算数据样本之间的相似度,并存储在相似度矩阵S中。
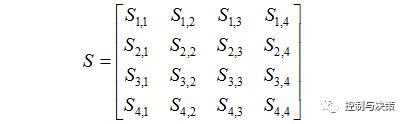
矩阵S中的元素Si,j是数据样本xi和xj的相似度,本文采用支持向量机的高斯核函数计算相似度,它对数据的非线性特征有较好的辨识能力。
AP算法将S作为原始输入数据,通过其信息处理机制筛选簇中心。S的对角线元素是数据样本xi与自己的相似度,通常为1,即数据样本与自己完全相似。AP算法将S的对角线元素称为偏向参数,也就是初始时各数据样本成为簇中心的概率,所以通常要将S对角线元素置为统一的一个概率值p,以表示各数据样本初始时成为簇中心的概率均相等。
2) 用概率无向图模型估计数据样本成为簇中心的概率。
首先为相似度矩阵S建立一个概率无向图模型。设定一个相似度的阈值m,如果元素Si,j≥m,表明样本xi和xj有相似性关系,在无向图矩阵M中用2表示;否则,表示样本xi和xj没相似性关系,在无向图矩阵M中用0表示。例如,数据集X一个可能的无向图矩阵如下示:
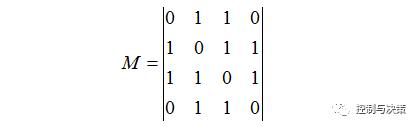
根据式(2)的M可画出一个概率无向图如图2所示。
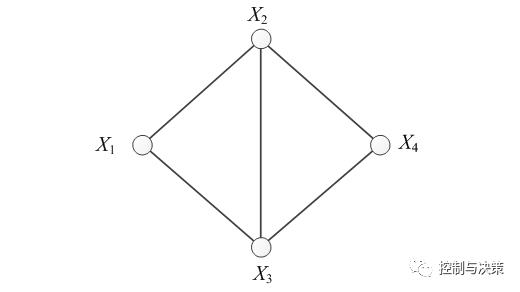
图2 M对应的概率无向图
按照极大团的原理,把图2的概率无向图拆分成两个极大团,如图3所示。一个极大团,是概率无向图的一个子图,特点是极大团中的节点两两有线连接,并且团中节点个数达到最大。
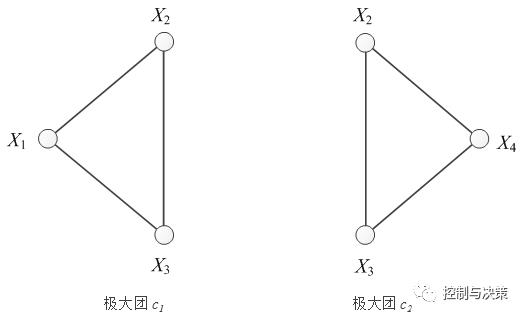
图3 从图2拆分出来的两个极大团
对于一个极大团,用势能函数可计算出团中各节点的概率密度,例如极大团c1中,节点x2的概率密度为P(x2|c1)=Ψc1(x2),其中Ψ(▪)是势能函数。同理,可计算出极大团c2中,节点x2的概率密度为P(x2|c2)=Ψc2(x2)。把节点x2在其出现的各极大团中的概率密度相乘,得到样本x2的最终概率密度P(x2)=P(x2|c1)* P(x2|c2)。用类似的方法,可以计算出其他3个样本的概率密度P(x1)、P(x3)、P(x4)。最后,把P(x1)、P(x2)、P(x3)、P(x4)按相应的顺序替换S矩阵对角线上的元素,实现用概率无向图估算样本的概率密度并注入到AP的偏向参数中,启发AP算法哪个样本更适合作为簇中心。
3成果的价值以及存在的不足
本文的实验结果表明,通过概率无向图模型给AP算法注入簇中心启发式信息后,AP算法的计算效率、聚类精度较传统AP算法有明显提高,思路是可行的。但实验中也发现,本文AP算法所得到的簇数目还是比真实簇数目多,所以AP算法计算结束后,补充了一段“簇归并”环节,把AP生成的簇再合并,最终得到的簇数目与真实簇数目基本相同。因此,如何使AP生成的簇数目更接近真实情况,是今后值得进一步研究的方向,它涉及到对AP内核信息处理机制进行改进。
作者介绍

覃华,教授,从事量子计算理论、近似动态规划最优化方法、数据挖掘等研究。

詹娟娟,硕士生,从事数据挖掘的研究。
苏一丹,教授,主要从事自然计算、电子商务、信息安全等研究。
本文作者隶属广西大学计算机与电子信息学院电子商务研究室,研究室有教授5名,副教授4名,中级职称1名。团队近年主要从事智能商务和最优化理论的研究,承担国家自然科学基金10余项,发表论文200余篇,获厅局级科技奖励10余项。近三年,团队的主要研究兴趣是概率图模型理论和正则化机器学习方法在电子商务中的应用。
以上是关于精彩文章推荐广西大学 覃华等:基于概率无向图模型的近邻传播聚类算法的主要内容,如果未能解决你的问题,请参考以下文章