常用聚类算法之一k-means实例解析

Posted 2021-04-09 天善大数据

学过聚类分析的朋友应该都认识K-MEANS算法吧，这是个无监督学习算法，也就是说事先并没有对样本进行标记，需要通过算法来自动确定，它有很多优点，简单快速，对大数据集有较好的效率等，当然也有缺点，最大的一个缺点个人认为是它没办法处理非球型的类别。

算法的基本步骤我也说说吧

1、首先先确定要为样本分几类（这个不是很好确定），然后为每个聚类确定一个初始的聚类中心，这样就有K个初始聚类中心；

2、然后根据最小距离原则为每个样本点划分归到最近的类别；

3、生成后的类别重新计算类别中心；

4、重复2，3步骤直至类别中心没有变化；

5、结束，得到了K个聚类。

    下面通过一个实例过程来带大家认识一下这个算法，因为自己一直秉承着只有实践才能深刻认识，在认识这个算法前先稍微介绍一下要用到的公式，我们选用欧式距离：表示点Xi和Xj他们之间的距离，距离越小，表示样本之间越相似，差异度越小，反之距离越大，样本之间的越不相似，差异度越大。

    

    那我们如何去评价聚类的好坏呢？我这时候就需要一个误差平方和准则Mi表示类别中心

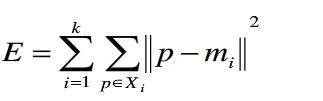
下面我们用一个实例来展示K-means算法的整个过程，在此我构造了一个数据，为了节省计算时间起见，构造了一个二维的数据集，并划分为2个类别，选取O1和O5为两个初始簇心

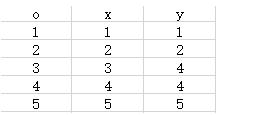
所以M1=O1=(1，1),M2=O5=(5，5);

然后计算剩余的每条记录，根据其与各个簇中心的距离将它划分给最近的簇

对于O2：

                

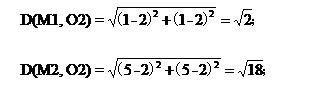
因为，所以O2这条记录分给了M1类，

对于O3:

                    

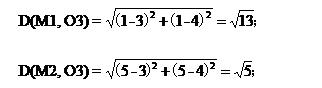
因为，所以O3这条记录分给了M2类，

对于O4：

                      

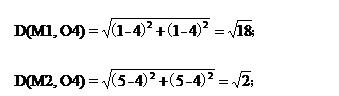
因为，所以O4这条记录分给M2；

因此我们得到了一个新的分类簇C1={O1，O2},C2={O3，O4，O5}

然后计算平方误差：

M1=O1=(1，1),

M2=O5=(5，5),

所以总体的平均方差是：E=E1+E2=2+7=9,这一轮结束，然后我们在迭代一次

计算新的簇心，M1=((1+2)/2,(1+2)/2)=(1.5，1.5)

                        M2=((3+4+5)/3,(4+4+5)/3)=(4,4.33)

然后我们重复上面计算距离的步骤；得到将O1和O2分给C1,O3，O4和O5分给了C2

得到C1={O1，O2}，C2={O3，O4，O5},

计算平方误差：

M1=O1=(1.5，1.5)，

M2=O5=(4，4.33),

所以总体的平均方差是：E=E1+E2=1+1.3467=2.3467，从第一次迭代后总体平均误由：9~2.3467，大幅度的得到了减少，然后在计算簇心，M1=((1+2)/2,(1+2)/2)=(1.5，1.5)

                                       M2=((3+4+5)/3,(4+4+5)/3)=(4,4.33)
 由于簇心未发生变化，迭代停止；
所以我们就得到了上面的聚类结果，这就是我们常用的聚类算法K-MEANS，过程有什么错误还请大家指正。

↓↓↓ 点击"阅读原文" 【查看作者更多文章】