聚类算法之K-means算法
Posted Microstrong
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了聚类算法之K-means算法相关的知识,希望对你有一定的参考价值。
目录:
(1)理解相似度度量的各种方法与相互联系(熟悉闵可夫斯基距离,其它作为了解)
(2)掌握K-means聚类的思路和使用条件
(一) 聚类的定义
聚类就是对大量未知标注的数据集,按数据的内在相似性将数据集划分为多个类别,使类别内的数据相似度较大而类别间的数据相似度较小。聚类是无监督学习。
(二) 相似度、距离计算方法总结
相似度跟距离是相反的概念。如果两个样本Xi与Xj ,它们的距离比较大,那么它们的相似度是比较小的。总之,我们有了相似度就能度量距离,有了距离就能度量相似度。
(1)闵可夫斯基距离
给定样本Xi = (Xi1;Xi2;Xi3;……Xin)与Xj=(Xj1;Xj2;Xj3;……Xjn),最常用的是“闵可夫斯基距离”,公式如下:
欧式距离:
当p=2时,闵可夫斯基距离即为欧式距离:
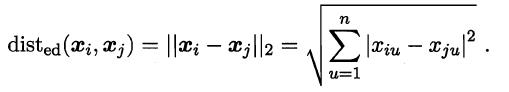
此时,上式也是Xi-Xj的L2范数,表示为:||xi-xj||2。
那么L2范数如何计算呢?我给大家演示一下,假如我们有两个样本X = (X1;X2;X3)与Y=(Y1;Y2;Y3),两个样本分别有三个特征,我们来计算一下这两个样本的欧式距离:
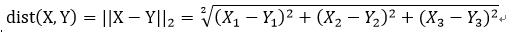
曼哈顿距离:
当p=1时,闵可夫斯基距离即为曼哈顿距离:
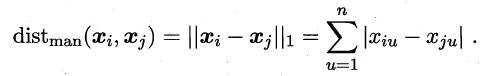
此时,上式也是Xi-Xj的L1范数||xi-xj||1。
那么L1范数如何计算呢?我给大家演示一下,假如我们有两个样本X = (X1;X2;X3)与Y=(Y1;Y2;Y3),两个样本分别有三个特征,我们来计算一下这两个样本的漫哈顿距离:
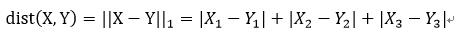
(2)杰卡德相似系数(Jaccard)
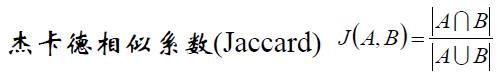
杰卡德相似系数可以这么理解:情景一:A代表对某个用户的推荐购物列表,B表示用户自己心目中喜欢的商品列表,现在我们要计算A集合和B集合的相似度,就用到了杰卡德相似系数。情景二:A表示的是A用户喜欢电影的列表,B表示B用户喜欢电影的列表。假如前一段时间《前任3》很火,A和B的列表里面都有,这个不能说明问题。但是同时发现A和B的列表里面还有其他比较冷门的电影,那么我们可以发现A和B的相似性突然增大了。杰卡德相似系数还可以用在降低热门商品,提高冷门商品的推荐上。
(3) 余弦相似度(cosine similarity)
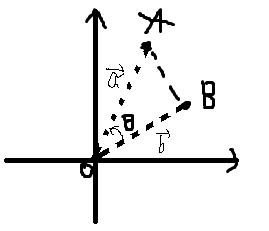
理解:求A点和B点的相似度,我们可以直接求A点到B点的距离。也可以求A点到原点和B点到原点的Cosθ的值。
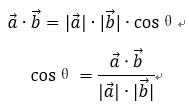
(4)Pearson相似系数
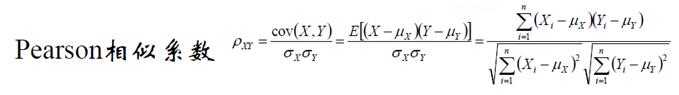
余弦相似度与Pearson相似系数关系:
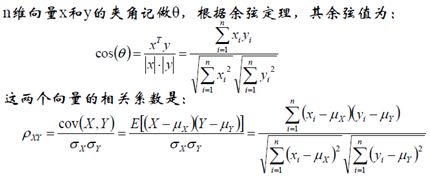
相关系数即X、y坐标向量各自平移到原点后的夹角余弦!这即解释了为何文档间求距离使用夹角余弦——因为这一物理量表征了文档去均值化后的随机向量间相关系数。
(5)相对熵(K-L距离)
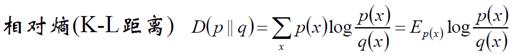
(6)Hellinger距离
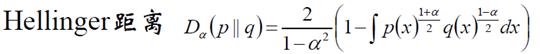
当α=0时候,我们做如下计算:
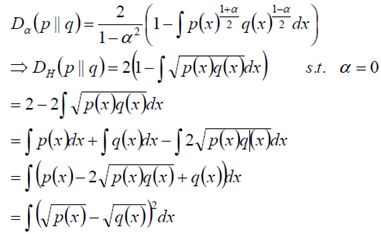
该距离满足三角不等式,是对称、非负距离。
(三)K-means算法
(1)聚类的基本思想
给定一个有N个对象的数据集,构造数据的K个簇,K<=n。满足下列条件:
每个簇至少包含一个对象。
每一个对象属于且仅属于一个簇。
将满足上述条件的k个簇称作一个合理划分。
基本思想:对于给定的类别数目K,首先给出初始划分,通过迭代改变样本和簇的隶属关系,使得每一次改进之后的划分方案都较前一次好。
(2)K-means的基本算法

学习完K-means算法之后,我们来思考几个问题?
1.K-means是能够得到全局最小值么?
对k个初始质心的选择比较敏感,容易陷入局部最小值。
2.K-means一定收敛么?
K-Means算法一定收敛。数据集比较大时,收敛会比较慢。想了解详细细节参考博客:http://blog.csdn.net/u010161630/article/details/52585764
3.K-means的k个初始均值向量如何选择呢?
对k个初始质心的选择比较敏感,容易陷入局部最小值。
改进:有人提出了另一个成为二分k均值(bisecting k-means)算法,它对初始的k个质心的选择就不太敏感。
4.K-means的k如何指定呢?
K值的选择是用户制定的,不同的k得到的结果会有挺大的不同。
改进:对k的选择可以先用一些算法分析数据的分布,如重心和密度等,然后选择合适的k。
(3)K-means的实现代码
from numpy import *
import xlrd
import matplotlib.pyplot as plt
# 计算欧氏距离
def euclDistance(vector1, vector2):
'''
:param vector1: 第j个均值向量
:param vector2: 第i个样本
:return: 距离值
'''
return sqrt(sum(power(vector2 - vector1, 2)))
# init centroids with random samples
def initCentroids(dataSet, k):
'''
:param dataSet: 数据集
:param k: 需要聚类的个数
:return: 返回k个均值向量
'''
numSamples, dim = dataSet.shape
centroids = zeros((k, dim))
for i in range(k):
index = int(random.uniform(0, numSamples))
centroids[i, :] = dataSet[index, :]
return centroids
# k-means cluster
def kmeans(dataSet, k):
'''
:param dataSet: 数据集
:param k: 需要聚类的个数
:return:
'''
# 样本的个数
numSamples = dataSet.shape[0]
# 第一列存储该样本所属的集群
# 第二列存储此样本与其质心之间的误差
clusterAssment = mat(zeros((numSamples, 2)))
clusterChanged = True
## step 1:从数据集中随机选择k个样本作为初始均值向量
centroids = initCentroids(dataSet, k)
while clusterChanged:
clusterChanged = False
## 循环每一个样本
for i in range(numSamples):
minDist = 100000.0 #存放最短的距离
minIndex = 0 # 第i个样本的簇标记
## 循环每一个均值向量
## step 2: 找到第i个样本的最近的均值向量
for j in range(k):
distance = euclDistance(centroids[j, :], dataSet[i, :])
if distance < minDist:
minDist = distance
minIndex = j
## step 3: 更新第i个样本的簇标记和误差
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist ** 2
## step 4: 更新均值向量
for j in range(k):
pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]
centroids[j, :] = mean(pointsInCluster, axis=0)
print ('Congratulations, cluster complete!')
return centroids, clusterAssment
# show your cluster only available with 2-D data
def showCluster(dataSet, k, centroids, clusterAssment):
numSamples, dim = dataSet.shape
if dim != 2:
print ("Sorry! I can not draw because the dimension of your data is not 2!")
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
if k > len(mark):
print ("Sorry! Your k is too large! please contact Zouxy")
return 1
# draw all samples
for i in range(numSamples):
markIndex = int(clusterAssment[i, 0])
plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']
# draw the centroids
for i in range(k):
plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=12)
plt.show()
def main():
## step 1: load data
print ("step 1: load data...")
dataSet = []
data = xlrd.open_workbook('C:/Users/Microstrong/Desktop/watermelon4.0.xlsx')
table = data.sheets()[0]
for line in range(0,table.nrows):
lineArr = table.row_values(line)
dataSet.append([float(lineArr[0]), float(lineArr[1])])
## step 2: clustering...
print ("step 2: clustering...")
dataSet = mat(dataSet)
k = 3
centroids, clusterAssment = kmeans(dataSet, k)
## step 3: show the result
print ("step 3: show the result...")
showCluster(dataSet, k, centroids, clusterAssment)
if __name__ == '__main__':
main()
(4)K-means算法的缺点和改进
1. K-means将簇中所有点的均值作为新质心,若簇中含有异常点,将导致均值偏离严重。即对噪声和孤立点数据比较敏感。
举个例子:
数组[1, 2, 3, 4, 100]的均值为22,显然距离“大多数”数据1、2、3、4比较远,若是改成求数组的中位数3,在该实例中更为稳妥。这种聚类方式即K-Mediods聚类(K-中值聚类)。
2. 初值的选择,对聚类结果有影响吗?如何避免呢?
k-means是初值敏感的
图(1)K-means初值选择不合理情况
假如左图中红色的点为初始的均值向量,那么聚类之后的结果可能为右图中的结果。那么聚类的结果肯定不是我们想要的结果。我们想要的结果肯定是图(2)所示的结果。造成聚类结果不理想的原因是我们的均值向量初始化的时候没有做好。那么如何解决这种问题呢?
图(2)理想的聚类结果
优化选初值的办法:K-means++算法
假如有50个样本,做4个簇的聚类,u1的选择肯定是从50个样本中随机选择一个。那么u2该如何选择呢?我们用50个样本中的每一个样本对u1作距离计算,得到50个距离数组。把这50个距离作为权重,我们算出权重概率,把权重概率高的那个距离对应的样本初始为u2。那么u2选择完之后,我们如何选择u3呢?我们再来把50个样本对u1和u2做距离计算,如果样本到u1的距离大于到u2的距离,更新距离数组里对应的值;如果样本到u1的距离小于到u2的距离,那么距离数组里对应的值保持不变。我们根据更新后的距离数组来做权重概率,找出权重概率最高点的作为u3。那么u4如何选择呢?我们用u3、u2、u1分别对50个样本作距离计算,找出最小距离值然后更新距离数组,找到权重概率最大对应的点就是u4了。
思考一个问题:为什么要更新距离数组呢?
u3选择时更新距离数组是为了选择u3的点要保证离u1和u2都要远。u4是同样的道理。
(5)K-means聚类算法总结
1. 优点:
(1)是解决聚类问题的一种经典算法,简单、快捷
(2)对处理打数据集,该算法保持可伸缩性和高效性
(3)当簇近似为高斯分布时,它的效果更好。
2. 缺点:
(1)在簇的平均值可被定义的情况下才能使用,可能不适用于某些应用
(2)必须事先给出K(要生成的簇的数目),而且对初值敏感,对于不同的初始值,可能会导致不同的结果。
(3)不适合于发现非凸形状的簇或者大小差别很大的簇
(4)对噪声和孤立点数据敏感
3.作用:
(1)可以作为其他聚类方法的基础算法,如谱聚类
Reference:
周志华《机器学习》
http://blog.csdn.net/zouxy09/article/details/17589329(参考代码)
以上是关于聚类算法之K-means算法的主要内容,如果未能解决你的问题,请参考以下文章