纯干货无监督核心聚类算法

Posted 2021-04-08 66号学苑

引言

开始讲解算法之前，我们先来看一个例子：假设有n种中药混在一起，我们想把这堆药材放在m个药匣中，且m < n。我们的要求是，装在一个药匣中的药材要有一些相似性，而药匣和药匣之间差异较大。我们该怎么做呢？我们可以把功效相似的放在一组，或者把名字字数相同的放在一起，或者，我们可以看形状的相似性，气味的相似性，价钱区间相同的放在一起等等，这里的功效、气味和价格等就是所谓的“特征”。除了让事物映射到一个单独的特征之外，一种常见的做法是同时提取 N 种特征，将它们放在一起组成一个 N 维向量，从而得到一个从原始数据集合到 N 维向量空间的映射——你总是需要显式地或者隐式地完成这样一个过程，因为许多机器学习的算法都需要工作在一个向量空间中。

现在，我们可以开始讨论算法了。

第一种 K-means

现在，我们暂时不去考虑原始数据的形式，假设我们已经讲其映射到了一个欧式空间上了，为了方便，我们用二维空间来展示，如下图所示：

图1 散点图

单纯用肉眼看，我们的大脑很快就能判断出，这些散点大致属于三个集群，其中两个很紧凑，一个很松散。我们的目的就是区分这些散点从属于哪个集群，同样为了方便，我们把三个集群图上不同的颜色，如下图所示：

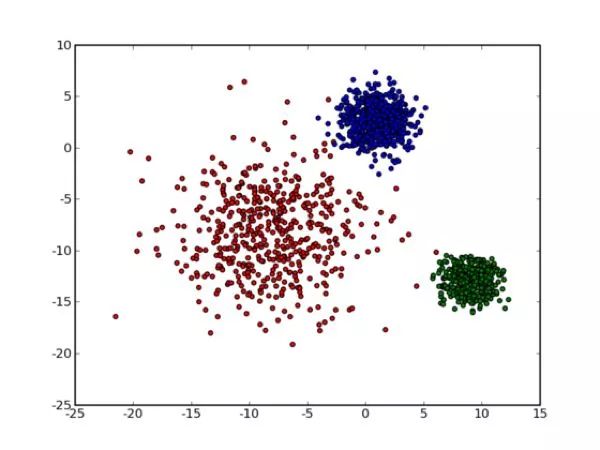
图2 被标注颜色的散点图

人的大脑可以扫一眼就分辨出的集群，计算机却不会这么轻易做到，它无法仅通过形状就“大致看出来”，这就需要用到我们马上要讲的算法K-means了。K-means基于一个假设：对于每一个集群（cluster），我们都可以选出一个中心点（center），使得该cluster中的所有点到该cluster中心点的距离小于到其他cluster中心点的距离。当然，实际情况可能无法总是满足这个假设，但这是我们能达到的最好结果，而那些误差通常是固有存在的或者问题本身的不可分性造成的。所以，我们暂且认为这个假设是合理的。

在此基础上，我们来推导K-means的目标函数：假设有N个点，要分为K个cluster，K-means要做的就是最小化：

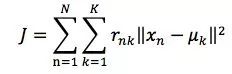
其中，rnk在数据点n被归类到clusterk时为1，否则为0。直接寻找rnk和μk来最小化J并不容易，不过我们可以采用迭代的办法，先固定μk，选择最优的rnk。可以看出，只要将数据点归类到离他最近的那个中心就能保证J最小。下一步则固定rnk，再求最优的μk。将J对uk求导并令导数等于0，很容易得到J最小的时候μk应该满足：

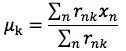
也就是uk的值应该是cluster k中所有数据点的平均值。由于每一次迭代都是为了取到更小的J，所有J会不断减小直到不变。这个迭代方法保证可k-means最终会达到一个极小值。

此处要做个说明，K-means不能保证总是能收敛到全局最优解，这与初值的选择有很大关系。因此在实际操作中，我们通常会多次选择初值跑K-means，并取其中最好的一次结果。K-means结束的判断依据可以是迭代到了最大次数，或者是J的减小已经小于我们设定的阈值。

总结一下，在众多聚类方法中，K-means属于最简单的一类。其大致思想就是把数据分为多个堆，每个堆就是一类。每个堆都有一个聚类中心（学习的结果就是获得这k个聚类中心），这个中心就是这个类中所有数据的均值，而这个堆中所有的点到该类的聚类中心都小于到其他类的聚类中心（分类的过程就是将未知数据对这k个聚类中心进行比较的过程，离谁近就是谁）。其实K-means算的上最直观、最方便理解的一种聚类方式了，原则就是把最像的数据分在一起，而“像”这个定义由我们来完成（类比把药材按照什么特征装入药匣） 。

第二种 高斯混合模型

下面，我们来介绍另外一种比较流行的聚类算法——高斯混合模型GMM（Gaussian Mixture Model）。GMM和K-means很相似，区别仅在于GMM中，我们采用的是概率模型P(Y|X)，也就是我们通过未知数据X可以获得Y取值的一个概率分布，我们训练后模型得到的输出不是一个具体的值，而是一系列值的概率。然后我们可以选取概率最大的那个类作为判决对象，属于软分类soft assignment（对比与非概率模型Y=f(X)的硬分类hard assignment）。

GMM学习的过程就是训练出几个概率分布，所谓混合高斯模型就是指对样本的概率密度分布进行估计，而估计的模型是几个高斯模型加权之和（具体是几个要在模型训练前建立好）。每个高斯模型就代表了一个cluster。对样本中的数据分别在几个高斯模型上投影，就会分别得到在各个类上的概率。然后我们可以选取概率最大的类所为判决结果。

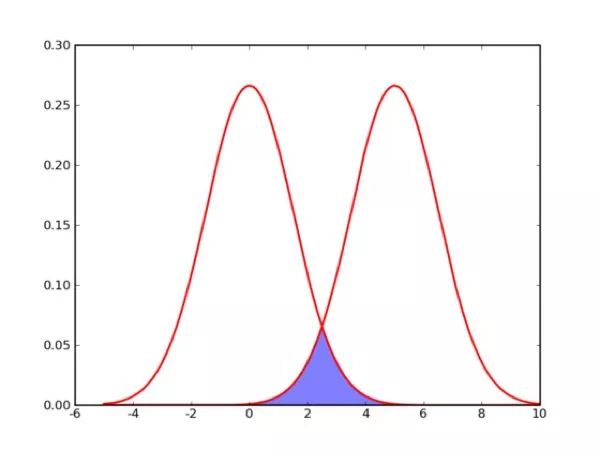
图3 两个高斯分布

得到概率有什么好处呢？拿下图中的两个高斯分布来说，(2.5,0) 属于其重合区域，它由两个分布产生的概率相等，你没办法说它属于那一边。这时，你只能猜测，选择2好像更好一点，于是你得出(2.5,0)属于左边的概率是51%，属于右边的概率是49%。然后，在用其他办法分别到底属于哪一边。可以想象，如果采用硬分类，分类的相似度结果要么0要么1，没有“多像”这个概念，所以，不方便多模型融合（继续判断）。

混合高斯模型的定义为：

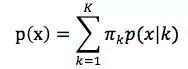
其中K为模型的个数，πk为第k个高斯的权重，p(x|k)则为第k个高斯的概率密度函数，其均值为μk，方差为σk。我们对此概率密度的估计就是要求πk、μk和σk各个变量。求解得到的最终求和式的各项结果就分别代表样本x属于各个类的概率。

在做参数估计的时候，常采用的方法是最大似然。最大似然法就是使样本点在估计的概率密度函数上的概率值最大。由于概率值一般都很小，N很大的时候这个连乘的结果非常小，容易造成浮点数下溢。所以我们通常取log，将目标改写成：

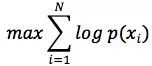
也就是最大化log - likelihood function，完整形式则为：

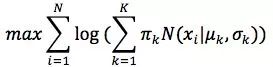
一般用来做参数估计的时候，我们都是通过对待求变量进行求导来求极值，在上式中，log函数中又有求和，若用求导的方法算，方程组将会非常复杂，所以我们不直接求导，而是采用EM（Expection Maximization）算法。这与K-means的迭代法相似，都是初始化各个高斯模型的参数，然后用迭代的方式，直至波动很小，近似达到极值。

总结一下，用GMM的优点是投影后样本点不是得到一个确定的分类标记，而是得到每个类的概率，这是一个重要信息。GMM每一步迭代的计算量比较大，大于k-means。GMM的求解办法基于EM算法，因此有可能陷入局部极值，这与初始值的选取十分相关。

第三种 层次聚类

不管是K-means，还是GMM，都面临一个问题，那就是k取几比较合适。比如在bag-of-words模型中，用k-means训练码书，那么应该选取多少个码字呢？为了不在这个参数的选取上花费太多时间，可以考虑层次聚类。

假设有N个待聚类的样本，对于层次聚类来说，基本步骤就是：

1. 把每个样本归为一类（初始化），计算每两个类之间的距离，也就是样本与样本之间的相似度；

2. 寻找各个类之间最近的两个类，把他们归为一类（这样类的总数就少了一个）；

3. 重新计算新生成的这个类与各个旧类之间的相似度；

4. 重复2和3直到所有样本点都归为一类，结束。

整个聚类过程其实是建立了一棵树，在建立的过程中，可以通过在第二步上设置一个阈值，当最近的两个类的距离大于这个阈值，则认为迭代可以终止。另外关键的一步就是第三步，如何判断两个类之间的相似度有很多种方法。这里介绍一下三种：

· Single Linkage：又叫做nearest-neighbor ，就是取两个类中距离最近的两个样本的距离作为这两个集合的距离，也就是说，最近两个样本之间的距离越小，这两个类之间的相似度就越大。容易造成一种叫做Chaining 的效果，两个cluster 明明从“大局”上离得比较远，但是由于其中个别的点距离比较近就被合并了，并且这样合并之后Chaining 效应会进一步扩大，最后会得到比较松散的cluster 。

· Complete Linkage：这个则完全是Single Linkage 的反面极端，取两个集合中距离最远的两个点的距离作为两个集合的距离。其效果也是刚好相反的，限制非常大，两个cluster 即使已经很接近了，但是只要有不配合的点存在，就顽固到底，老死不相合并，也是不太好的办法。这两种相似度的定义方法的共同问题就是指考虑了某个有特点的数据，而没有考虑类内数据的整体特点。

· Average linkage：这种方法就是把两个集合中的点两两的距离全部放在一起求一个平均值，相对也能得到合适一点的结果。Average linkage的一个变种就是取两两距离的中值，与取均值相比更加能够解除个别偏离样本对结果的干扰。

以上这几种聚类的方法叫做agglomerative hierarchical clustering（自下而上），描述起来比较简单，但是计算复杂度比较高，为了寻找距离最近/远和均值，都需要对所有的距离计算个遍，需要用到双重循环。另外从算法中可以看出，每次迭代都只能合并两个子类，非常慢。

另外有一种聚类方法叫做divisive hierarchical clustering（自上而下），过程恰好是相反的，一开始把所有的样本都归为一类，然后逐步将他们划分为更小的单元，直到最后每个样本都成为一类。在这个迭代的过程中通过对划分过程中定义一个松散度，当松散度最小的那个类的结果都小于一个阈值，则认为划分可以终止。

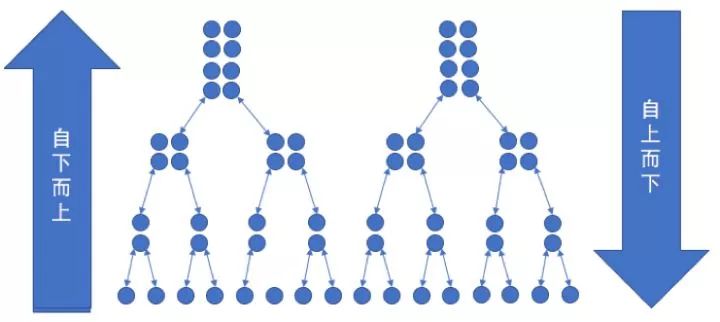
图4 自上而下和自下而上的层次聚类

由于这种层次结构，普通的K-means也被称为一种flat clustering。

以上三种方法为无监督算法常用的聚类算法，可以根据数据情况选择适用的算法。事实上，在算法的选择上也十分有讲究，不仅要考虑数据维度，数据类型，还要考虑数据分布等等。

来源|知乎

作者|DataVisor黄姐姐

ps:明天66号学苑将上线黄姐姐内容为“无监督学习在反欺诈中的应用”的风控课程，大家敬请关注哦～

更多精彩，戳这里：

点击阅读原文，即可报名