机器学习常用聚类算法大盘点，包括：原理使用细节注意事项

Posted 2021-04-08 Python与算法社区

后台回复 wuenda 获取鼻祖的最精简ML入门课, 回复 cs224 获取斯坦福NLP和深度学习的全部课程，回复数字 3 查看ML完整地由浅到深地学习笔记。

1 聚类

无监督学习是没有标记信息的学习方式，能够挖掘数据之间的 内在规律 ，聚类算法的目的就是找到这些数据之间的内在性质和规律。

它将数据划分为几个互不相交且并集为原集的子集，每个子集可能对应于一个 潜在概念 ，例如：购买力强的顾客、待配送的商家群体。

2 基本假设

聚类算法的核心是 通过距离计算来表征两个样本之间相似程度 。一般而言，距离的度量有几个原则：

1) 非负性：如果 ，表明距离是非负的，这是符合实际的。

2) 同一性：如果 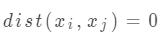，只有一种可能，表示两个点是重合的。

3) 对称性：如果 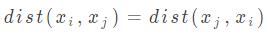，则说明距离具有对称性，但是在实际问题中，可能距离不具备这个性质，比如轿车导航路线从旧宫到北大的距离，与北大到旧宫的距离可能不等。

4) 直递性：这个也是距离非常重要的一个性质，是说距离满足，三角形两边之和大于第三边。形象地说，本计划从家想直接到学校，但是中间想去超市买瓶水然后再到学校，除非三点在一条线上，否则一定要多走路程。

以上关于距离的性质就是接下来要讨论的聚类算法的一些基本假设。下面介绍几种常用的聚类算法，之前已经推送过关于聚类算法的几篇文章，今天再提炼总结，顺便排版做得更好些，更方便大家学习。

3 聚类算法

3.1 K-Means

这个算法可能是大家最熟悉的聚类算法，简单来说， 选取初始中心点 ， 就近吸附到中心点 ， 迭代这一过程直到各个中心点移动很小为止 。接下来，我们详细讨论k-means算法在实际应用中的一些注意事项。

注意事项
k-means需要输入划分簇的个数，这是比较头疼的问题，为了应用它得先用别的算法或者不断试算得出大致数据可分为几类。这可能只是带来一些麻烦，还不能说是缺陷。不过，k-means算法的确存在如下 缺陷：

首先，它对初始中心点的选取比较敏感，如果中心点选取不恰当，例如随机选取的中心点都较为靠近，那么最后导致的聚类结果可能不理想。为了避免，通常都要尝试多次，每次选取的中心点不同一次来保证聚类质量, sklearn中实现了这种初始化框架k-means++. 关于这个机制可参考论文：

k-means++: The advantages of careful seeding

其次，K-means是通过吸附到中心点的方法聚类，它的基本假定: 簇是凸集且是各向同性的，但是实际中并不总是这样，如果簇是加长型的，具有非规则的多支路形状，此时k-means聚类效果可能一般。

最后，在高维空间下欧拉距离会变得膨胀，这就是所谓的 “维数诅咒” 。为了缓解此问题，通常k-means聚类前要使用PCA等降维算法，将多特征集中表达在低特征空间中，同时加快聚类收敛。

3.2 Mini Batch K-Means

K-means算法每次迭代使用所有样本，这在数据量变大时，求解时间就会变长。为了降低时间复杂度， 随机选取b个样本形成一个mini-batch ，这种算法就是 mini-batch k-means.它也是随机选取初始点，然后就近吸附到中心点，更新中心点直到移动很小为止。

虽然每次迭代只是抽样部分样本，但是聚类质量与k-means相比差不太多。

3.3 Mean Shift

mean shift 的聚类过程大致描述如下：在多维空间中，任选一个点，然后以这个点为圆心，h为半径做一个高维球，圆心与落在这个球内的每个点形成向量，然后把这些向量相加求和，结果就是Meanshift向量。

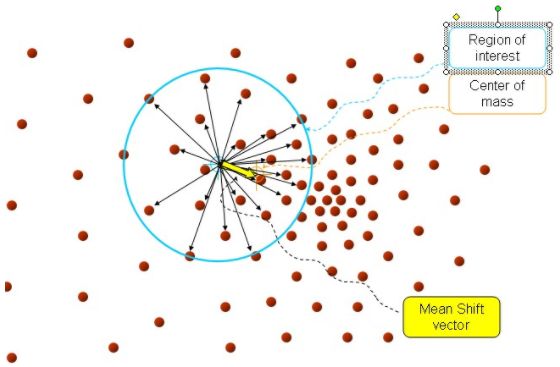
再以meanshift向量的终点为圆心再生成一个球。重复以上步骤，就再可得到一个meanshift向量。

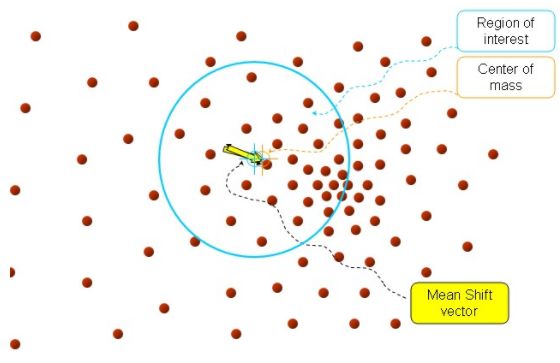
不断迭代，meanshift算法可以收敛到概率密度最大的区域，也就是最稠密的部分。

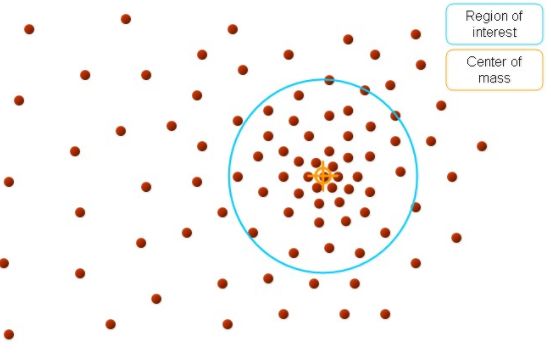
mean shift 算法需要知道 bandwidth ，也就是宽度(或理解为直径)。在sklearn中实现也实现了这个算法，它需要输入bandwidth，如果不输入此值，算法默认计算一个bandwidth.

3.4 层次聚类

层次聚类算法的基本思想：将m个样本看做 m个已经划分好的子集 ，找出距离最近的两个聚类子集并将它们合并，不断重复这个过程，直到剩余k个子集。

它是分治法思想的代表。

聚类的层次结构可以用一颗树来表达，根节点是一个包括所有样本的簇，叶子节点仅含有一个样本。

层次聚类常用的merge策略包括：

1) Ward  最小化簇间的均方误差，这点和k-means思想不谋而合。

2) Maximum or complete linkage  最小化两个簇间距的最大值，这个目标和支持向量机的目标函数有点相似。

Average linkage  最小化所有簇对间的间距。

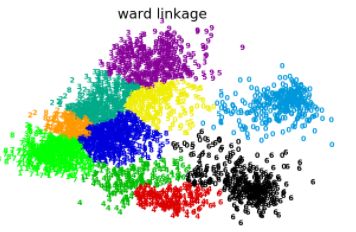
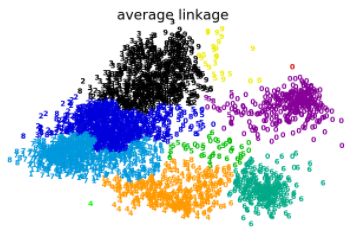
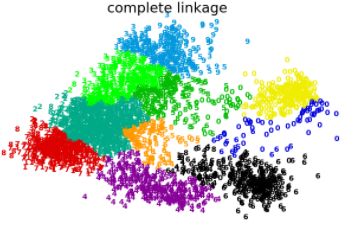
3.5 DBSCAN

DBSCAN算法将高密度区域视为由与低密度区域所分离，因此dbscan可以 发现任何形状的簇 ，优于k-means只能发现凸形状的簇。dbscan算法认为，如果某个样本满足：在一定距离（ eps ）内的能发现一定个数( min_samples )的样本，称它为核心对象(core sample)，非核心对象是eps范围内找不到满足一定数量的样本。

那么，构成一个簇的对象(或样本)一定是核心对象吗？如果是这样，这个簇将会无限递归下去而无法终止，由此可以直观上感知，一个簇的边缘一定是非核心对象，但是至少距离一个核心对象小于eps.如下图箭头所指对象，很小的圆圈代表非核心对象，但是它们至少离一个大圆(核心对象)距离小于eps.

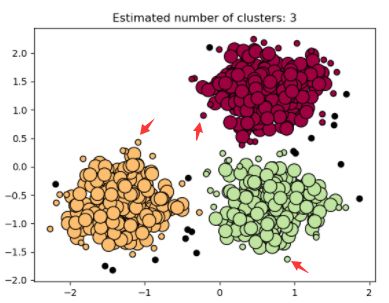
还有一类点，如上图中的黑点表示的非核心对象，它们不属于任何一个簇，言外之意，它们离任何一个簇距离至少eps，这类样本就是 奇异点(outliers)

dbscan算法在实际使用中会发现它与读入 样本的顺序相关 ，顺序会影响到非核心对象所吸附到的簇。如果一个非核心对象离不同簇的两个核心对象距离都小于eps，此时非核心对象被吸附到的簇是首先被扫描到的核心对象所属的簇。

还有一处值得留意，为了计算某个样本的近邻域，如果构造距离矩阵，内存消耗n^2，为了避免内存消耗，可以构建kd-trees或ball-tress，但是对于稀疏矩阵就不能应用这些算法，但是有一些其他措施可以解决。

综上，dbscan需要输入eps和min_samples作为算法的两个入参。

3.6 高斯混合

一般地，假设高斯混合模型由K个高斯分布组成，每个高斯分布称为一个component，这些 component 线性组合在一起就构成了高斯混合模型的概率密度函数：

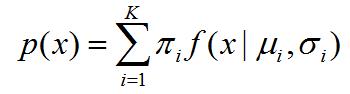
上式就是GMM的概率密度函数，可以看到它是K个高斯模型的线性叠加，其中每个高斯分布对GMM整体的概率密度所做的贡献为系数 。

GMM首先要确定数据样本 x 来自于component k的概率，可以理解为样本 x 对component k做的贡献，并且component k 又对整体的GMM做贡献，这样间接地样本 x 对整体的GMM做了一些贡献，这样带出了；然后再用最大似然估计确定所有的样本点对component k 的影响进而获得分布参数：均值和方差，一共确定这3个参数。

关于高斯混合模型的不调包详细模型代码实现参考之前推送：

后台回复数字 3

4 聚类评估

聚类算法的结果好坏可以用adjusted rand index，数学模型等，更详细的参考：

http://scikit-learn.org/stable/modules/clustering.html#clustering-performance-evaluation

这部分可以单独抽出一篇文章来写，后续推送。

文章用心血凝聚，不走捷径，如不反感可否<点广告点赞>支持下， 这样我会更加坚定初心，更有勇气在这条"与别人不一样"的艰辛原创之路上一直走下去 …