跟着“海哥”学AI丨二分K均值聚类算法
Posted 新华三大数据
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了跟着“海哥”学AI丨二分K均值聚类算法相关的知识,希望对你有一定的参考价值。
上一期我们从鸢尾花的故事展开,介绍了基于鸢尾花数据集的经典K-mean聚类算法的基本原理和应用,这期我们将继续给大家带来K-means聚类算法的另一个变体,即改进的二分K均值(Bisecting K-means)。
第三课:二分K均值聚类算法
前面通过鸢尾花数据集聚类问题,我们了解到K-means聚类算法的思想,这是一种非常直观简单的聚类算法,不过该算法有一个明显的缺点就是对初始值比较敏感,很容易陷入局部最优解,而不能达到全局最优聚类,影响聚类效果即分类不准。参看下图:
如左图中选择的初始值不好,聚类的结果会如右图所示效果不好。若初始簇心选取不好时会直接影响聚类的效果,所以K-Mean是对初始值敏感的。
为了克服这个问题,一种常用的解决方法(还有其他方法)是使用k-means算法的改进算法,即二分k均值(Bisecting k-means)聚类算法。
算法原理如下:
将所有的点组成一个簇,然后将该簇一分为二,即执行k=2的聚类(即每一次簇分裂,保持两个簇的结果不变时,才会进行下一次簇分裂);
将能最大程度降低聚类代价函数(也就是误差平方和,Sum of Squared Error,SSE)的簇分裂为两个簇(即选取一个误差最大的簇进行分裂);
重复2,直到分裂出的簇数等于用户指定的聚类数(即输入K参数)为止。
二分k均值(bisectingk-means)是一种结构性聚类(层次聚类)方法,其实质就是满足整体SSE最小的情况下,不断的对选中的簇做k=2的k-means切分以达到聚类数等于用户指定的聚类数目k为止。
聚类的误差平方和能够衡量聚类效果的好坏,该值越小表示数据点越接近于它们的质心(有的也称作簇心),聚类效果就越好。所以我们就需要对误差平方和最大的簇进行再一次的划分,因为误差平方和越大,表示该簇聚类越不好,越有可能是多个簇被当成一个簇了,所以我们首先需要对这个簇进行拆分。
以新华三人工智能引擎为例,二分k均值聚类算法作为其机器学习可视化的一个组件,通过拖放等操作即可直接使用,在上一期鸢尾花数据集的例子上,增加二分k均值算法聚类组件,如下图所示:
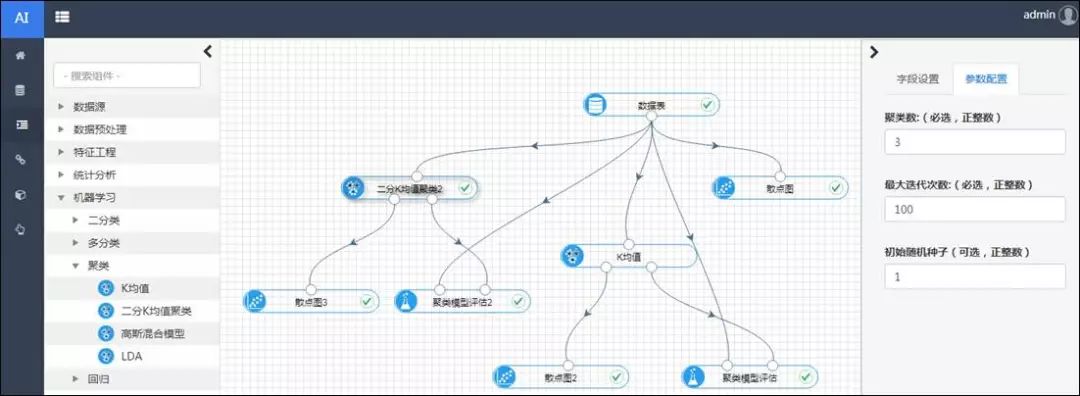
运行后查看聚类中心和评估结果:
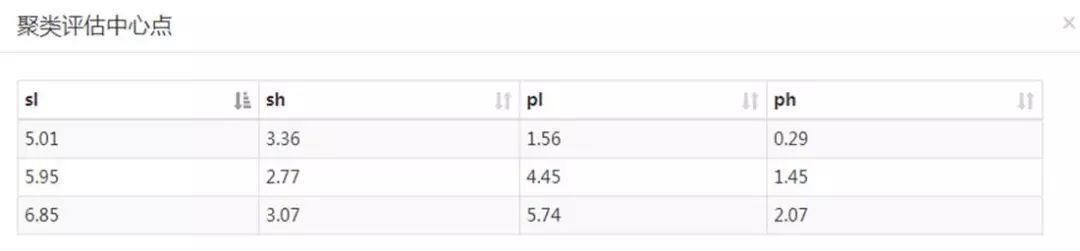
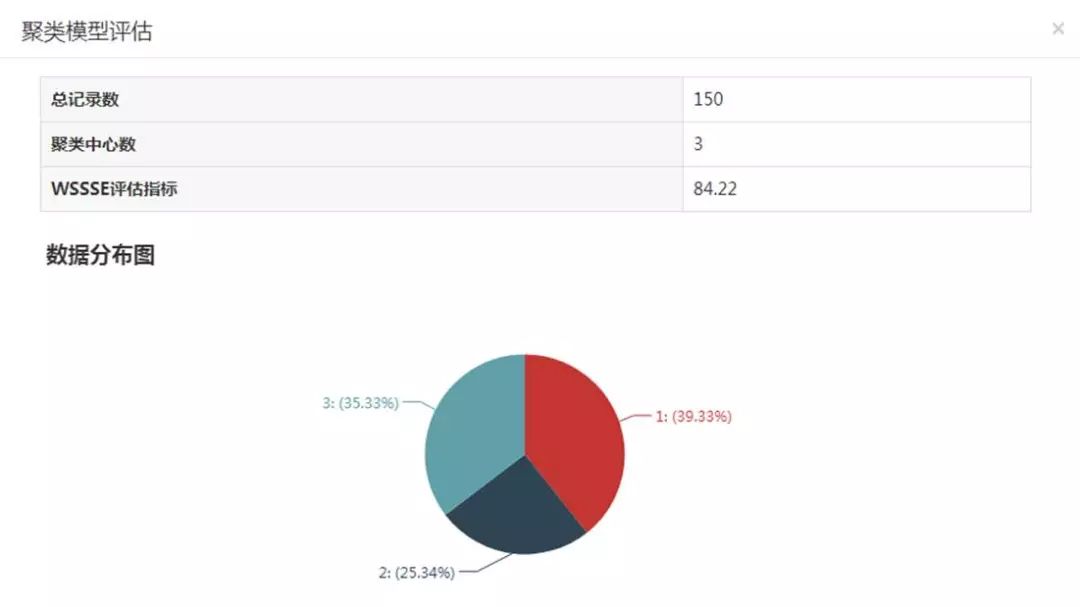
二分K均值算法可以加速K-means算法的执行速度,同时不受初始化问题的影响,结果相对较优,不过它和k-means算法一样,异常点的影响也比较大,不适用于不同尺寸和密度的类型的簇,也不适用于非球形簇(每个簇自聚成球形,高内聚低耦合,不是下面的球形)的聚类等。就不适合的场景如下图所示:
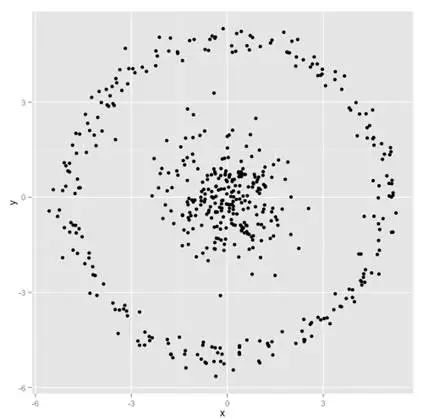
上面的划分,理想的聚类应该是内圈聚成一类,外环聚成一类。
数据算法本身来说是有局限性和适合的场景,优化后二分K-means算法比原K-means初始值敏感度会有所降低,但是至于敏感度会降低多少,数据科学家需要根据数据本身的特点进行测试或者实验,再选择合适的算法解决实际应用的问题。
往期链接:
以上是关于跟着“海哥”学AI丨二分K均值聚类算法的主要内容,如果未能解决你的问题,请参考以下文章