人工智能算法——K均值聚类算法Python实现

Posted 2021-04-08 书圈

K均值聚类算法实现

本文节选自《人工智能习题解析与实践》

1） 算法说明

K均值聚类算法是一种简单的迭代型聚类算法，采用距离作为相似性指标，从而发现给定数据集中的K个类，且每个类有一个聚类中心，即质心，每个类的质心是根据类中所有值的均值得到。对于给定的一个包含n个d维数据点的数据集X以及要分得的类别K,选取欧式距离作为相似度指标。聚类目标是使得各类的聚类平方和最小，即最小化：

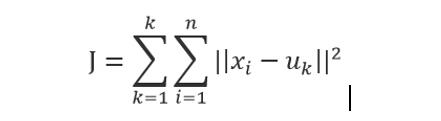
K-means是一个反复迭代的过程，算法分为四个步骤：

 

（1）选取数据空间中的K个对象作为初始中心，每个对象代表一个聚类中心；

 

（2）对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；

 

（3）更新聚类中心：将每个类别中所有对象所对应的均值作为该类别新的聚类中心，计算目标函数的值；

 

（4）判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回步骤（2）。

 

2）程序实现

以下是K均值法的python代码实现。程序使用的工具包括numpy和matplotlib，其中numpy是一个用于处理多维数组的库，而Matplotlib 则用于绘制二维图形。

 

# -*- coding: UTF-8-*-
import numpy   #用于处理多维数组的库import random  #用于生成初始质心
import codecs   #用于读取数据集文本并且解码import re      #利用正则表达式来整理输入数据的格式import matplotlib.pyplot as plt #绘制二维图形的库

# 计算向量vec1和向量vec2之间的欧氏距离def calcuDistance(vec1, vec2):
    return numpy.sqrt(numpy.sum(numpy.square(vec1- vec2)))

def loadDataSet(inFile):
    # 载入数据测试数据集
    # 数据由文本保存，为二维坐标
    inDate = codecs.open(inFile, 'r', 'utf-8').readlines()
    dataSet = list()
    for line in inDate:
        line = line.strip()    #  

        strList = re.split('[ ]+', line)  # 去除多余的空格
        # print strList[0], strList[1]
        numList = list()
        for item in strList:
            num = float(item)
            numList.append(num)
        # print numList
            dataSet.append(numList)

    return dataSet  #dataSet = [[], [], [], ...]

# 初始化k个质心，随机获取
def initCentroids(dataSet, k):
    return random.sample(dataSet,k)  # 从dataSet中随机获取k个数据项返回

def minDistance(dataSet, centroidList):
    # 对每个属于dataSet的item，计算item与centroidList中k个质心的欧式距离，找出距离最小的，
    # 并将item加入相应的簇类中
    clusterDict = dict() # 用dict来保存簇类结果
    for item in dataSet:
        vec1 = numpy.array(item)  #转换成array形式
        flag = 0  # 簇分类标记，记录与相应簇距离最近的那个簇
        minDis = float("inf")  # 初始化为最大值

        for i in range(len(centroidList)):
            vec2 =numpy.array(centroidList[i])
            distance =calcuDistance(vec1, vec2)  # 计算相应的欧式距离
            if distance < minDis:
                minDis = distance
                flag = i  #循环结束时，flag保存的是与当前item距离最近的那个簇标记
            if flag not in clusterDict.keys():  #簇标记不存在，进行初始化
               clusterDict[flag] = list()
        # print flag, item
             clusterDict[flag].append(item)  #加入相应的类别中
    return clusterDict  # 返回新的聚类结果

# 得到k个质心
def getCentroids(clusterDict):
    centroidList = list()
    for key in clusterDict.keys():
        centroid =numpy.mean(numpy.array(clusterDict[key]), axis=0)  #计算每列的均值，即找到质心
        # print key, centroid
        centroidList.append(centroid)

    return numpy.array(centroidList).tolist()

def getVar(clusterDict, centroidList):
    # 计算簇集合间的均方误差
    # 将簇类中各个向量与质心的距离进行累加求和
    sum = 0.0
    for key in clusterDict.keys():
        vec1 =numpy.array(centroidList[key])
        distance = 0.0
        for item in clusterDict[key]:
            vec2 = numpy.array(item)
            distance +=calcuDistance(vec1, vec2)
        sum += distance
    return sum

# 展示聚类结果def showCluster(centroidList, clusterDict):
    colorMark = ['or', 'ob', 'og', 'ok', 'oy', 'ow']  # 不同簇类的标记 'or' --> 'o'代表圆，'r'代表red，'b':blue
    centroidMark = ['dr', 'db', 'dg', 'dk', 'dy', 'dw']  # 质心标记 同上'd'代表棱形
    for key in clusterDict.keys():
        plt.plot(centroidList[key][0],centroidList[key][1], centroidMark[key], markersize=12)  # 画质心点
        for item in clusterDict[key]:
            plt.plot(item[0],item[1],colorMark[key])  # 画簇类下的点
    plt.show()

if __name__ == '__main__':

    inFile = "D:Pythonpracticekmean.txt"  # 数据集文件
    dataSet = loadDataSet(inFile)  #载入数据集
    centroidList = initCentroids(dataSet, 3)  #初始化质心，设置k=3
    clusterDict = minDistance(dataSet,centroidList)  # 第一次聚类迭代
    newVar = getVar(clusterDict, centroidList)  #获得均方误差值，通过新旧均方误差来获得迭代终止条件
    oldVar = -0.0001  #开始时均方误差值初始化为-0.0001
    print('***** 第1次迭代 *****')
    print()
    print('簇类')
    for key in clusterDict.keys():
        print(key, ' --> ', clusterDict[key])
    print('k个均值向量: ',centroidList)
    print('平均均方误差: ',newVar)
    print(showCluster(centroidList,clusterDict))  # 展示聚类结果

    j = 2  #
    while abs(newVar- oldVar) >= 0.0001:  # 当连续两次聚类结果小于0.0001时，迭代结束
        centroidList = getCentroids(clusterDict)  #获得新的质心
        clusterDict = minDistance(dataSet,centroidList)  # 新的聚类结果
        oldVar = newVar
        newVar = getVar(clusterDict,centroidList)

        print('***** 第%d次迭代 *****' % j)
        print()
        print('簇类')
        for key in clusterDict.keys():
            print(key, ' --> ', clusterDict[key])
        print('k个均值向量: ',centroidList)
        print('平均均方误差: ',newVar)

        print(showCluster(centroidList,clusterDict))         # 展示聚类结果

        j += 1

3）数据验证

现在假设有9个坐标点数据，它们分别是（3,2）、（3,9）（8,6）（9,5）（2,4）（3,10）（2,5）（9,6）（2,2）。利用上面的程序来计算它的簇，设定在计算开始时随机选择三个点作为初始质心，并且要求聚类结果必须小于0.0001。

程序运行的字符界面输出的结果如下图13.3和图13.4所示。

 

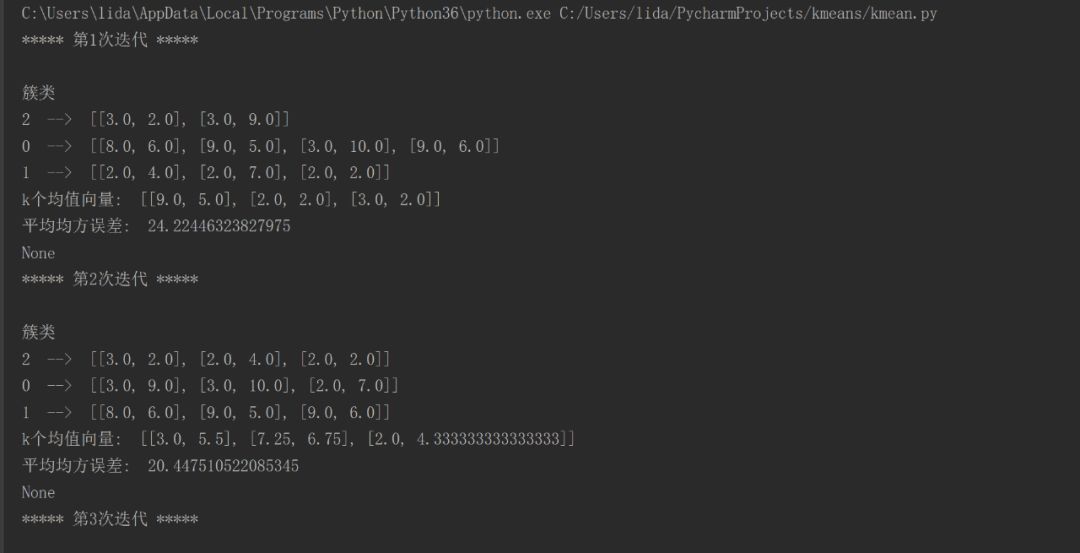
图13.3  程序运行的字符界面输出的结果

 

图13.4  程序运行的字符界面输出的结果（续）

 

程序调用python的绘图包输出图形界面的结果如下图13.5、图13.6和图13.7所示。从这几个图中可以看到簇类和簇心的变化。

图13.5展示的迭代开始时，随机选择的簇心。

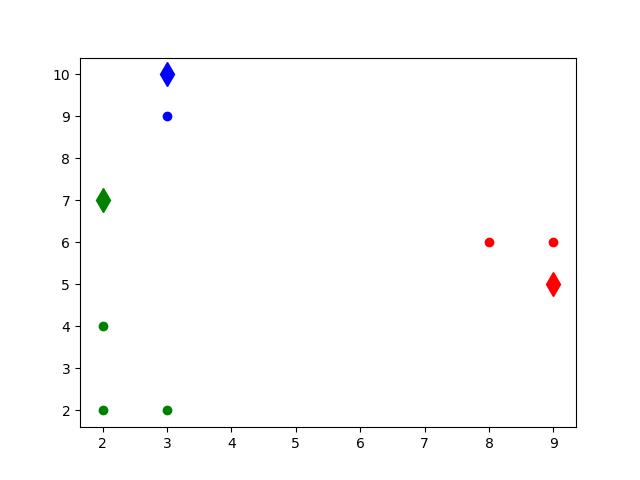
图13.5 第一次迭代，随机选择的簇心

图13.6展示第二次迭代后，簇心发生变化，平均均方误差减小（从图13.4可以看出）。

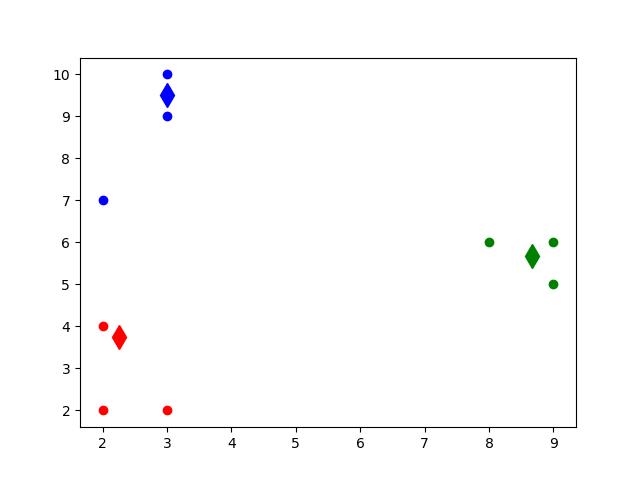
图13.6 第二次迭代后，簇心的发生变化

 

图13.7展示第三次迭代后，簇心进一步发生变化，平均均方误差更小（从图13.4可以看出）。

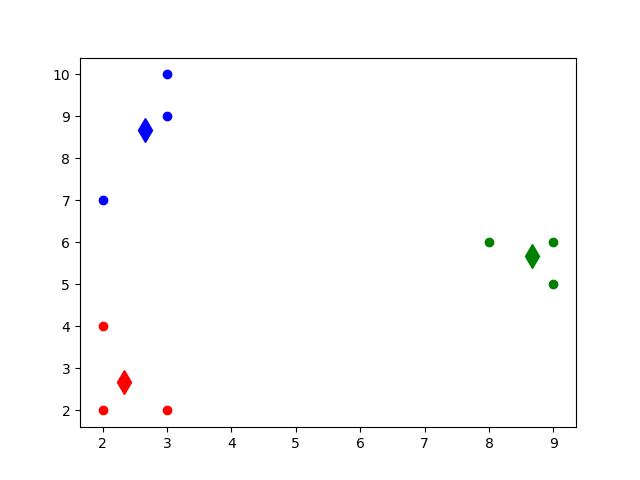
图13.7第三次迭代后，簇心进一步发生变化

从图13.4可以看出，第4次迭代与第三次迭代的结果是相同的，因此迭代4次后，程序终止执行。

4）程序说明

(1)在计算机安装了python之后，还需要安装numpy和matplotlib。这两个工具包分别是帮助进行科学运算并且根据计算结果绘制图的。

dataset=loadDataSet(inFile)

就是完成这个功能。

(3)数据集加载完成后，由函数initCentroids来进行质心的初始化。在本程序中，使用了random函数来从数据集中随机抽取若干个质心，而质心的数量可以由第二个参数来设定。本程序设定的质心数量为3个。

(4)整理好的数据集和随机选取的质心会作为参数，交给函数minDistance进行聚类迭代计算。在这个计算里面，使用了定义的calcuDistance函数来计算点到点之间的欧式距离。

(5)最后利用上一步的结果，使用函数getVar来计算簇集合间的均方误差。

(6)控制迭代结束的条件是，在main函数中利用两次聚类的结果只差小于0.0001。

 

 

扫码，优惠购书

定价：59元

ISBN：9787302458876

本书系统地阐述了人工智能的基本原理、实现技术及其应用，全面地反映了国内外人工智能研究领域的最新进展和发展方向。全书共19章，分为4个部分：第1部分是搜索与问题求解，用8章的篇幅系统地叙述了人工智能中各种搜索方法求解的原理和方法，内容包括状态空间和传统的图搜索算法、和声算法、禁忌搜索算法、遗传算法、免疫算法、粒子群算法、蚁群算法和Agent技术等；第2部分为知识与推理，用4章的篇幅讨论各种知识表示和处理技术、各种典型的推理技术，还包括非经典逻辑推理技术和非协调逻辑推理技术；第3部分为学习与发现，用3章的篇幅讨论传统的机器学习算法、神经网络学习算法、数据挖掘和知识发现技术；第4部分为领域应用，用3章分别讨论专家系统开发技术和自然语言处理原理和方法。

扫码，优惠购书

定价：69.80元

ISBN：9787302519669

本书作为作者已出版多次的《人工智能》教材的配套教辅材料，其章节与原教材基本对应，但内容分为学习目标与要求、知识要点、原教材对应的习题解析、补充题、课堂演示与实验指导5个部分。其中，学习目标与要求为每章要达到的学习目标；知识点与原教材的内容对应，基本上全面介绍了人工智能的理论与技术；习题解析对每章的习题进行了解答；补充题对原教材的习题进行了补充，并给出了解答。