一文了解k-means聚类算法

Posted 2021-04-08 AIrange

之前的课程，我们学习了线性回归、逻辑回归、k-近邻算法、SVM、朴素贝叶斯、决策树、随机森林的算法，这些算法有一个共同点就是，它们都是监督学习的算法，即训练样本的标记信息是已知的，数据是有标签的。

而相对地，也有非监督学习算法，该算法所用的数据无标签。我们不会告诉算法某个数据属于哪一类，它会自己找出关系，无需帮助。

今天我们将学习一个非监督算法——k均值（k-means）聚类算法，内容将有以下几部分：

1、什么是非监督学习
2、什么是聚类算法
3、什么是k-means聚类
4、k-means聚类算法的工作过程
5、k-means聚类算法的应用

k-means聚类算法

什么是非监督学习

概念

非监督学习是解决一些我们不知道结果应该是什么样的问题。它只基于输入的数据来发现模式，当我们非常不确定在寻求什么的时候这个技术非常有用。

非监督学习的数据没有标签，目标是为了揭露训练样本的内在属性，结构和信息。

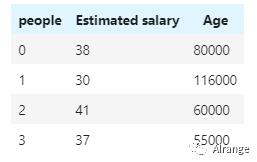
如下图的数据集，最后一列purchased即用户是否有意愿购买汽车，0代表不购买，该列可以作为标签，我们可以利用监督学习的方法来训练模型，使得模型通过预估薪水和年龄来预测它的购买意向。

然而再看下图的数据，可能由于现实情况，我们得到的数据缺少先验知识，也就是没有标签，但我们依然可以用数据来挖掘信息，这里就可以用到非监督学习。

非监督学习的常见应用一：异常检测。检测异常的信用卡转账以防欺诈，或者在训练之前自动从训练集去除异常值。异常检测的系统使用正常值训练的，当碰到新实例，它可以判断这个新实例是否像正常值或异常值。

非监督学习的常见应用二：关联性规则学习。目标是挖掘大量数据以发现属性间有趣的关系。例如，发现买了烧烤酱和薯片的人也会买牛排，因此可以将这些商品放在一起。

非监督学习的类型

降维：目的是简化数据、但是不能失去大部分信息，即通过找到共同点来减少数据集的变量，做法之一是合并若干相关的特征，也就是特征提取。降维可以使计算机运行的更快，占用的硬盘和内存空间更少，也许可以提升性能。例如，汽车的里程数与车龄高度相关，降维算法就会将它们合并成一个。

非监督学习最典型的一个类型为聚类。

什么是聚类算法

聚类算法的目的就是将数据点划分为不同的团体里，并且使一个点和同一个集群里的点的相似度要比它和其他集群的点的相似度要大。

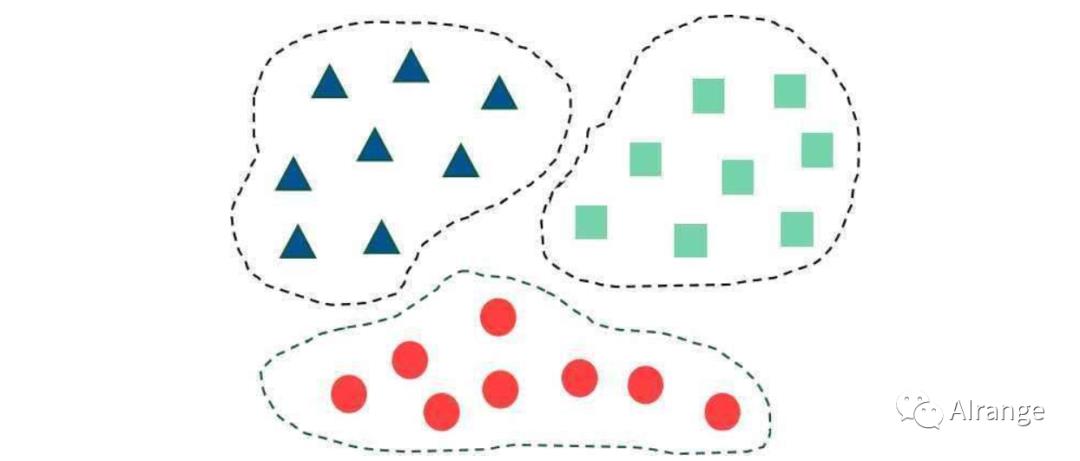
聚类算法包括k-means聚类、密度聚类、层次聚类等，今天讲的是k-means聚类算法。

什么是k-means聚类

k-means聚类算法又称k均值算法，在这个算法中，我们将把实体分为不相交的k个簇，同一个簇中的所有实体之间尽可能地相似，并且不在同一个簇的实体尽可能不相似。

距离测算（例如欧式距离）常被用于计算数据点之间的相似度和差异性。

距离测算（例如欧式距离）常被用于计算数据点之间的相似度和差异性。

k-means聚类如何工作

1、最初代表k个簇的中心点是在数据域中随机选取的。(本例k=3）

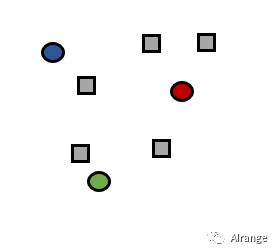
2、通过将每个样本与离它最近的中心点相关联，形成了k个簇。

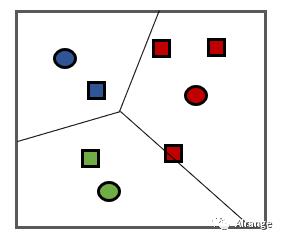
3、通过找到k个簇中各自的样本点的平均值，将其作为新的中心点。（图中虚线的点为原来的中心点）

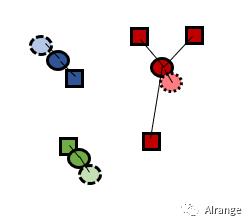
4、新的簇形成。第二步和第三步一直重复直到中心点的变化幅度小于某个阈值。

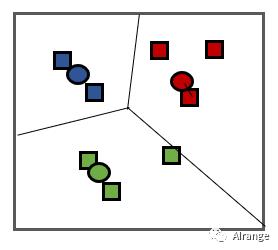
k-均值聚类的目标是最小化总的簇内方差，是衡量内部聚类的方式的指标。

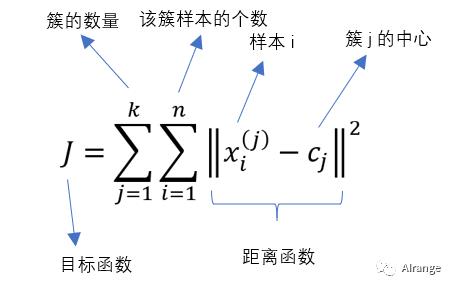
该公式刻画了簇内样本围绕簇中心点的紧密程度，该值越小表示簇内样本相似度越高。

再通过一个例子熟悉上述的步骤：

比如下图的数据要分两类（标准化之后的数据），k=2：

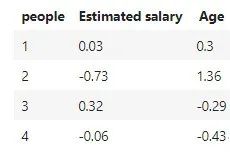
①随机选取两个簇的中心，假设为1和3号，即(0.03,0.3),(0.32,-0.29)

②样本2距离两个中心的距离分别为1.304和1.956，因此样本2被划入簇1中，同理，通过计算样本4被划入类别2中。

③于是形成这样的两个簇，(样本1，样本2)，(样本3，样本4)

④根据这两个新的簇，重新计算中心点，得到(-0.35,0.83),(0.13,-0.36)

通过新的簇中心来重新将样本划分，不断重复，直到中心点的变化小于阈值。

k-means聚类算法的应用

数据预处理

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

X = dataset.iloc[:, [0, 1]].values

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X = sc.fit_transform(X)

调用k-means聚类

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, random_state=0)
y_pred = kmeans.fit_predict(X)

n_clusters为k的值

查看kmeans模型的属性

①查看每个样本的所属的簇类别：

kmeans.labels_

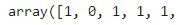
前五个样本被划分的簇编号如上图。

②查看每个簇的中心:

kmeans.cluster_centers_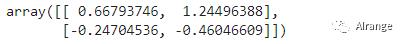

③样本到其最近的聚类中心的平方距离的总和：

kmeans.inertia_

可视化

from matplotlib.colors import ListedColormap
X_set, y_set = X, y_pred
for i, j in enumerate(np.unique(y_set)):#标记j和索引i
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],#类别标记 j 获取所有类别为j的点的横坐标和纵坐标
                c = ListedColormap(('blue', 'yellow'))(i), label = j)
plt.title('K-means')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()

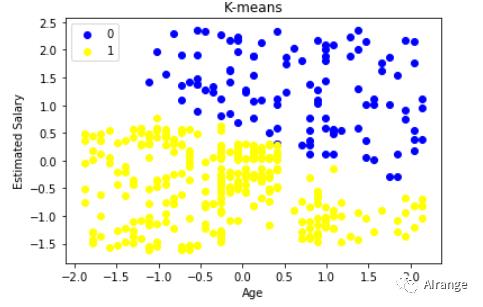
评估聚类模型的分数

由于是无监督学习，我们用来聚类的数据没有标记，该如何评估聚类模型的好坏呢？
我们可以用簇内的稠密程度和簇间的离散程度来评估聚类的效果，常见的方法为：

1、Silhouette Coefficient:轮廓系数
单个样本的轮廓系数计算公式如下图

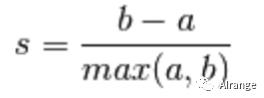
a：样本与它同簇的其他样本的平均距离，b：样本与下一个最近的簇中所有其他点之间的平均距离。

该模型的轮廓系数为所有样本的轮廓系数的平均值，值∈[-1,1],越大则聚类效果越好

from sklearn.metrics import silhouette_score
print(silhouette_score(X, y_pred,metric='euclidean'))

该模型的轮廓系数为约为0.383。

2、Calinski-Harabasz Index：

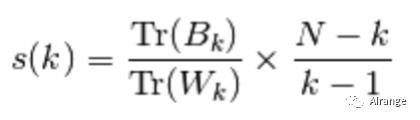
其中N为训练集样本数，k为类别数。Bk为类别之间的协方差矩阵，Wk为类别内部数据的协方差矩阵，Tr为矩阵的迹。

当群集密集且分隔良好时，分数会更高。

from sklearn.metrics import calinski_harabasz_score
print(calinski_harabasz_score(X, y_pred))

该模型的CH指数约为232.88。

参考资料：

https://github.com/Avik-Jain/100-Days-Of-ML-Code

机器学习——周志华

https://scikit-learn.org/modules/clustering.html

精彩内容回顾：

编辑：Sunam