聚类算法（谱聚类）

Posted 2021-04-08 数学 算法 生活

1.聚类问题可分为Compactness和Connectivity

2.Compactness只能处理凸集，典型是K-means

3.Connectivity典型代表是谱聚类，它是带权重的无向图

4.谱聚类利用切图原理寻找优化函数

5.引入指示向量Y、度矩阵D、邻接矩阵W来化简目标函数

上一篇我们介绍了K-means聚类算法，实际上，聚类问题可以分为两种思路：第一种是Compactness，这类算法只能处理凸集，GMM就属于这种；第二种是Connectivity，能很好处理非凸集，这类的代表就是谱聚类（Spectral Clustering），这一篇我们就介绍这个聚类算法。

模型介绍

谱聚类是一种基于带权重的无向图方法，它也是一种概率图模型。这个图用G=(V,E)表示，V是所有顶点的集合，E是边的集合。比如下面的无向图：

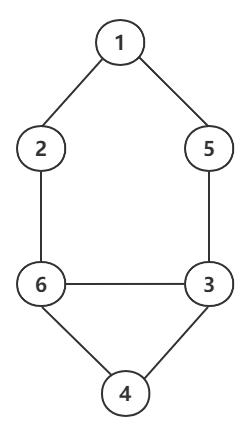
V是所有样本的集合,E代表两两样本的权重：

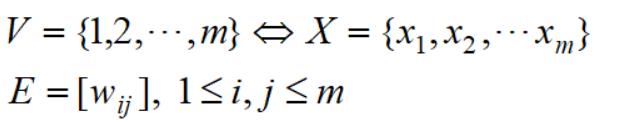
由于是无向图，所以

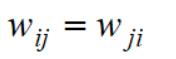
权重w用相似度度量，引入矩阵W：

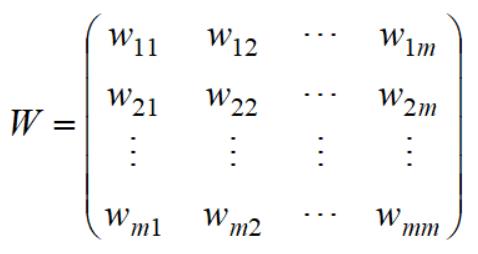
该矩阵称为相似度矩阵或邻接矩阵。表达了两两样本之间的权重。

相似度，通过用核函数度量，我们在文章介绍了几种核函数，这里由于是无向图，边代表了权重，如果没有边连接，则权重为0，于是：

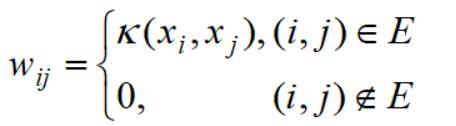
那么对于无向图是如何聚类的呢?假设我们已经完成了聚类，聚类的结果是这样的：

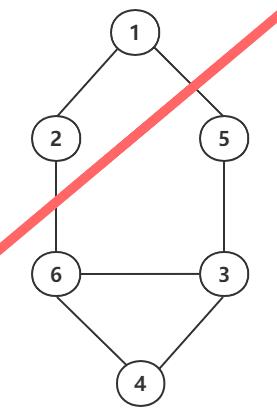
即：样本1,2作为一类，样本3~6作为另一类。

引入Cut:

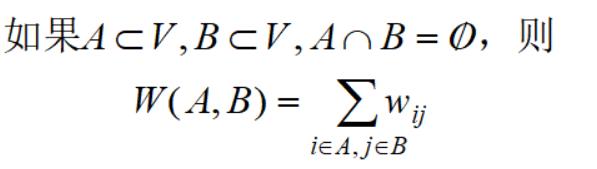
针对上面无向图，Cut的意思是说，样本1和样本2作为一类，它的每一个样本与第二类所有样本（样本3~6）的权重之和等于多少，这个实际上就是相对于尚未分割之前，整体的权重减少了多少，也就是代价（Cost）.

由此，我们对V聚类可得：

我们聚类的目标函数就是最小化Cut(V)：

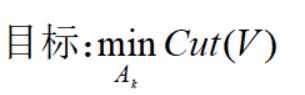
但直接采用上面式子不太合理，因为每个Ai的元素不一样会影响其权重之和，我们要归一化操作，引入单个节点的度：

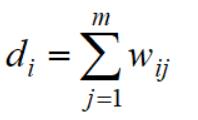
进而定义每个类别（集合）的度：

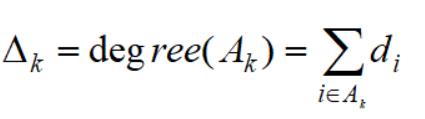
所以我们改进了目标函数，称为NCut:

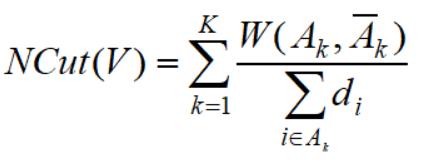
最终的优化问题就是最小化NCut

模型矩阵

上一节我们推导了最小化目标函数：

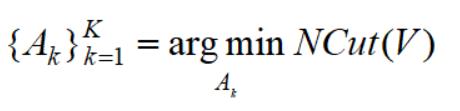
这一节我们对目标函数做变换，得到一种简洁的矩阵形式。为此，引入指示向量：

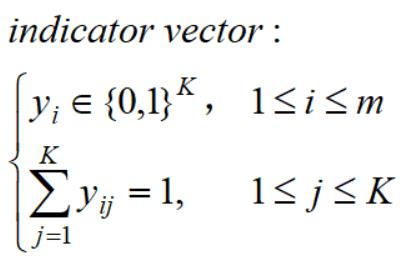
yi是K维的向量，每个维度取值0或1，并且只有一个1；它的意思是指，第i个样本属于第j个类别：

记Y:

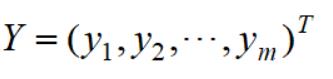
显然，Y是m*K维矩阵。优化目标转化为：

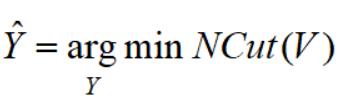
对NCut进行变换：

下面我们就用已知（W、Y）来表示矩阵O和P。先来看P。

因为：

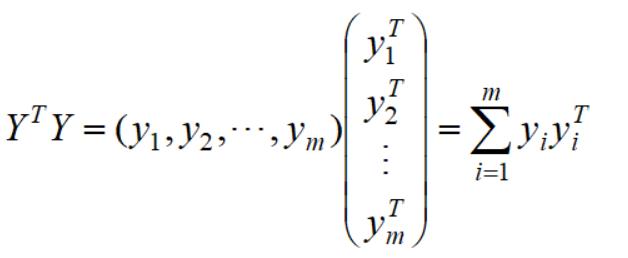
仔细观察向量yi的取值，可以知道：

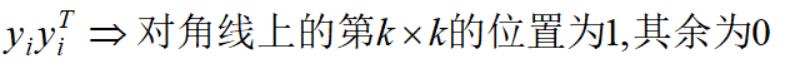
进一步，记属于类别k的样本数为Nk个，那么

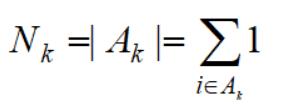
于是得到：

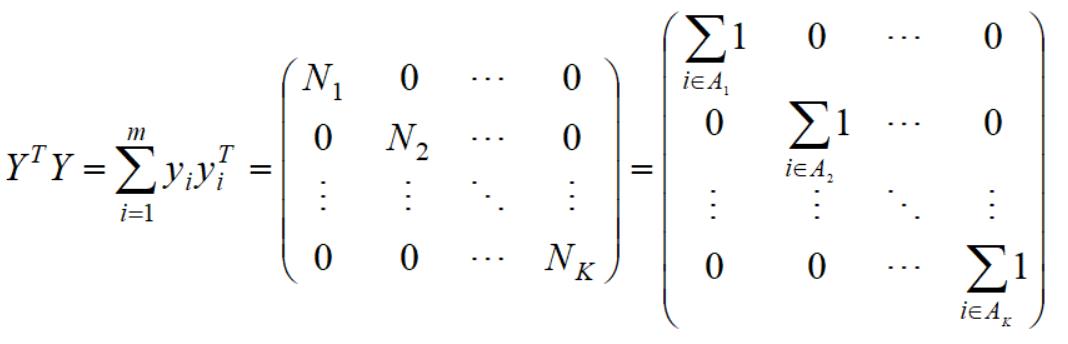
引进D(所以样本单个节点度构成的矩阵):

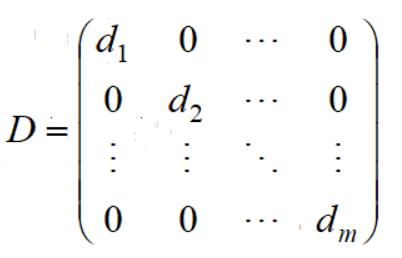
我们得到：

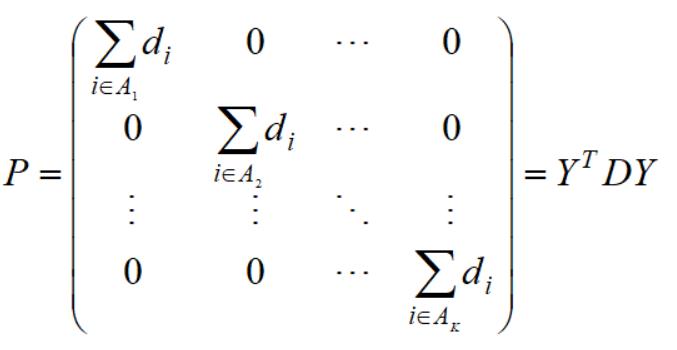
接下来我们来化简矩阵O:

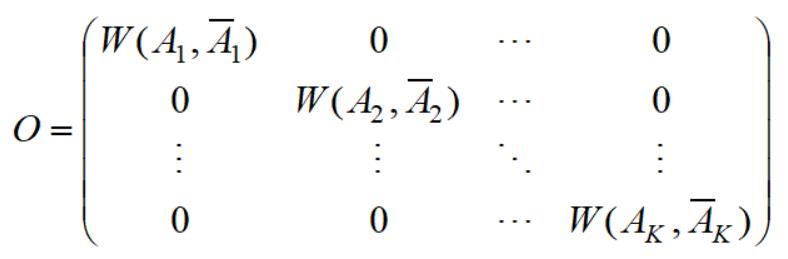
因为

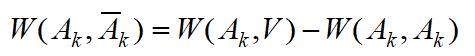
所以

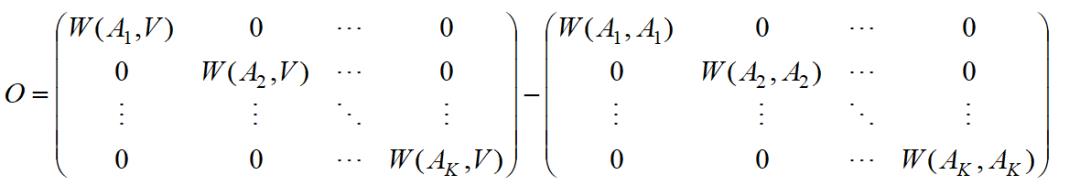
第一项实际就是矩阵P:

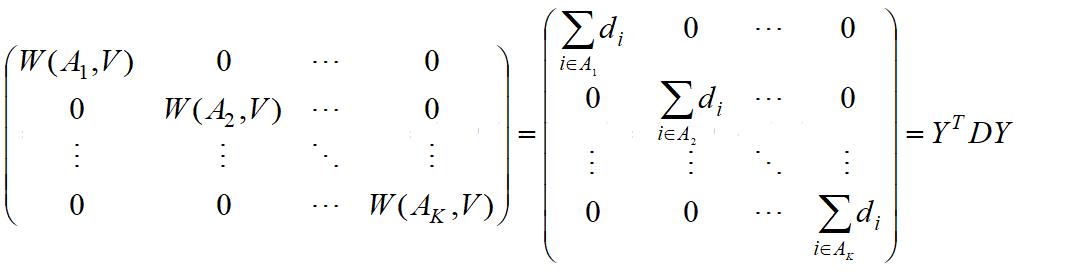
对于第二项，因为：

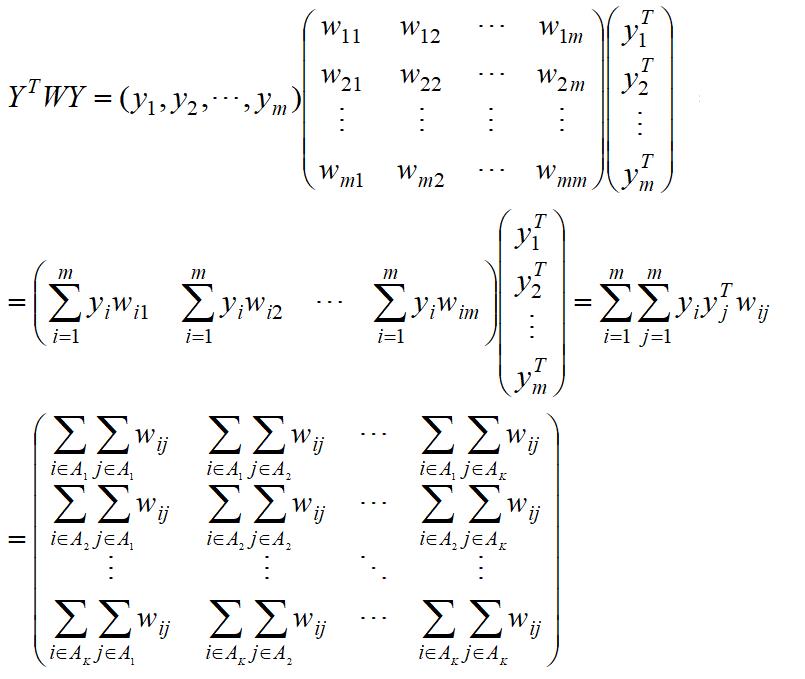
其对角与第二项完全一致，又因为最终目标函数是求矩阵的迹,若记

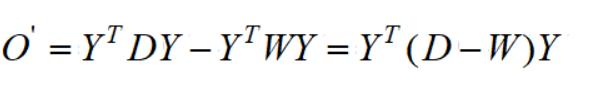
则：

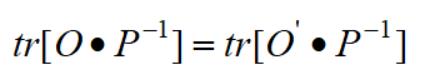
于是

我们得到最终优化的目标函数形式：

其中，L=D-W称为拉普拉斯矩阵。