贝塞尔曲线的几个知识点

Posted 2023-05-04

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了贝塞尔曲线的几个知识点相关的知识，希望对你有一定的参考价值。

参考技术A

1、贝塞尔曲线（Bézier curve）又被称为贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线，它的数学基础是伯恩斯坦多项式（Bernstein polynomial，since 1912），在1959年法国数学家Paul de Casteljau提出了数值稳定的 de Casteljau算法，开始贝塞尔曲线的图形化应用研究。

2、贝塞尔曲线的名称来源于一位就职于雷诺的法国工程师Pierre Bézier ，他在1962年开始对贝塞尔曲线做了广泛的宣传，他使用这种只需要很少的控制点就能生成复杂平滑曲线的方法来进行汽车车体的工业设计。

3、 Bezier曲线的递推算法"de Casteljau算法":

4、定点：曲线的起始点和结束点统称为定点。

3阶贝塞尔曲线沿线长等距分割方法

1、引言

贝塞尔(bezier)曲线又称样条曲线，常用的有2阶跟3阶形式，3阶曲线最为常用，其公式（1）为：

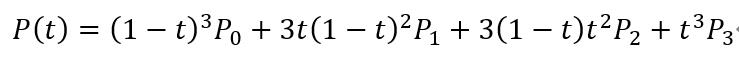
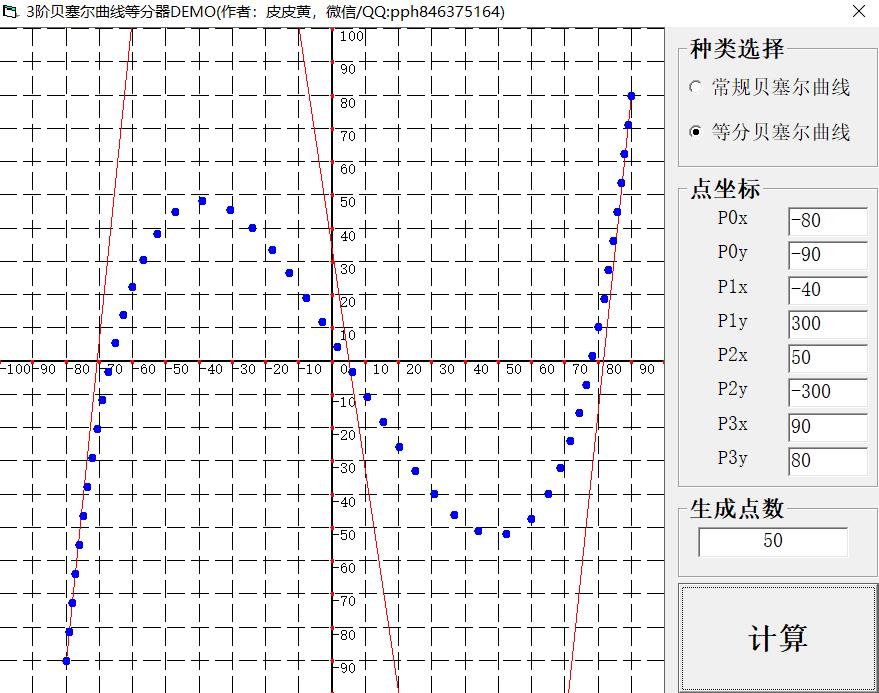
P0/P1/P2/P3为其四个控制点，贝塞尔曲线基础知识站内有相当详细地讲解博文。沿t进行等分，做出的曲线如下图蓝色点所示：

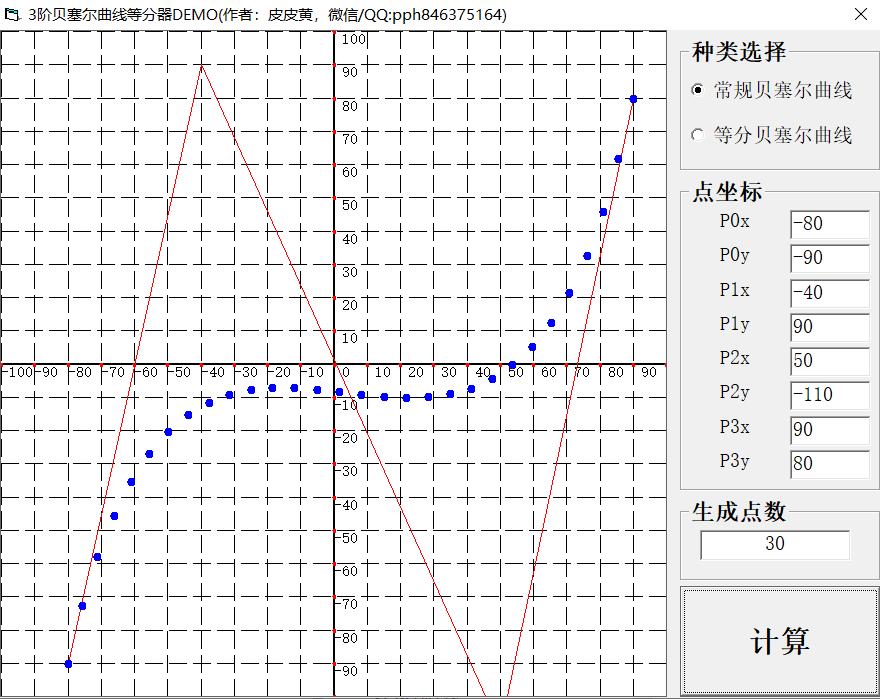
生成的点在沿曲线线长方向上，并不是均匀的。本文意在解决这个问题，实现线长方向上均匀的效果，如下图所示：

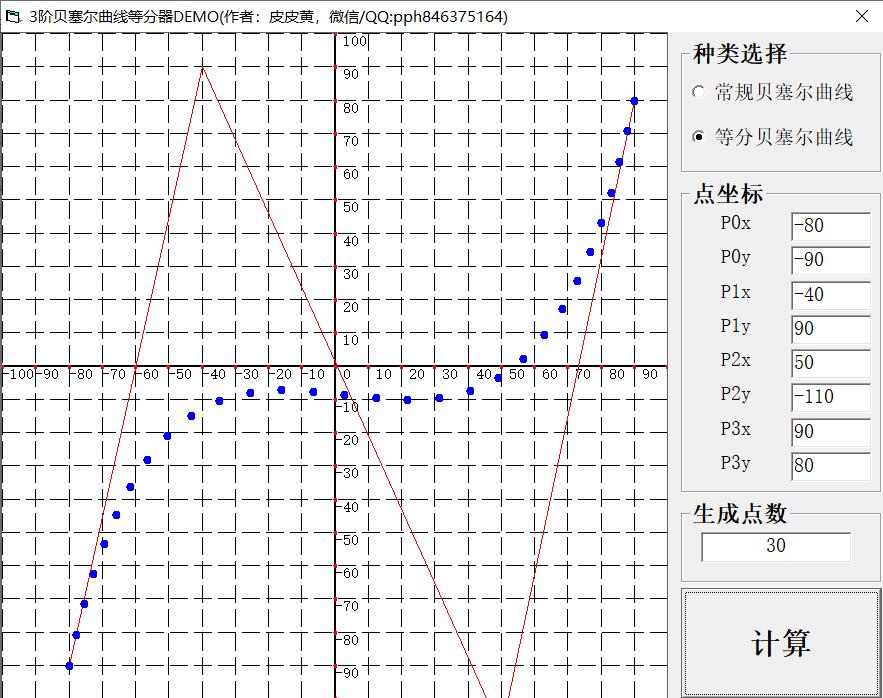
2、数学计算

将（1）式展开，转换为关于t的方程得到（2）式：

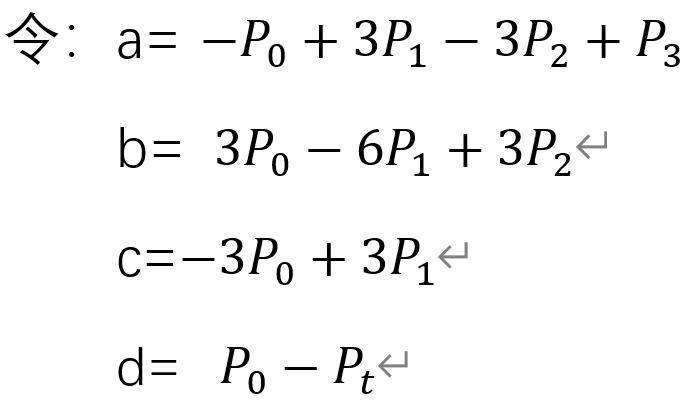
则（2）式简化为（3）式：

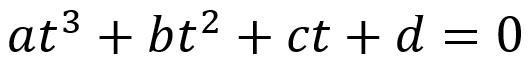
将（3）式展开到X,Y方向则有：

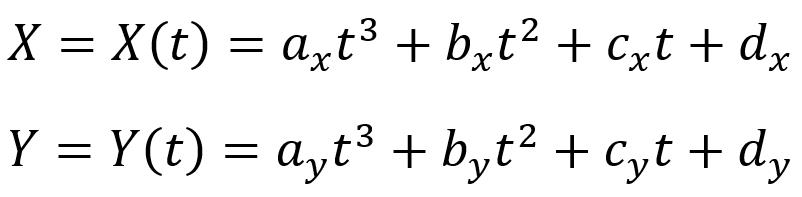
根据第二类曲线线长积分公式（4）：

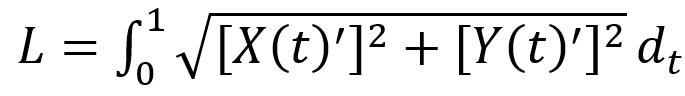
（4）式经过计算后可简化为：

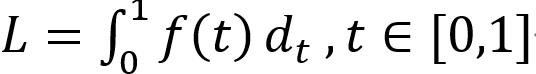
其中：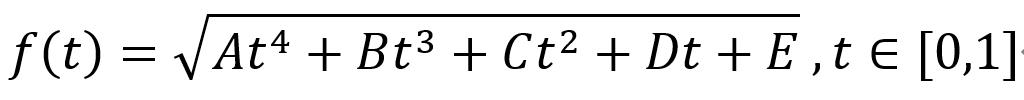
从0积分到1,得到L，即为3阶贝塞尔曲线的长度。将L分为N段，每次从0开始积分到L/N长度为止得到一个点，该点即为沿线长方向上一个等距划分点。至此，该问题转换为一个求定积分计算。
f(t)的原函数F(t)一般而言是不容易求出的，故采用数值积分的方法，求数值解。
求解定积分比较快速的方法是龙贝格公式，配合二分法或者切线法可以求得等分点对应的t值，最终实现等分效果。