用c语言编程 1创建图的邻接矩阵和邻接表 2验证图的深度优先、广度优先遍历算法 3验证最短路径

Posted 2023-05-04

求完整的实验报告啊有结果截图的那种啊，急求，谢谢啊

参考技术A 这些是c++的代码不知是否满足你的要求。
1、邻接表表示的图中分别用DFS和BFS遍历
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 图的邻接表的结点
struct Edge

int dest; // 目标结点下标
// int value; // 路径长度
Edge *link; // 下一个结点
;
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 为图添加一条边
// Input: edge - 欲加边的结点; dest - 目的结点
// Output: edge - 加边后的结点
// Tags:
void AddEdge(Edge *&edge, int dest)

// 简单的链表操作
if (!edge)

edge = new Edge;
edge->dest = dest;
edge->link = 0;

else

Edge *tail = edge;
while (tail->link) tail = tail->link;
tail->link = new Edge;
tail = tail->link;
tail->dest = dest;
tail->link = 0;


///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: Console下输入图的边
// Input: Graph - 图; n - 图的结点的个数; EdgeNumber - 添加边的个数;
// Output: Graph - 添加边后的图
// Tags: 用户输入点对(a, b), 表示添加a->b的路径
void Input(Edge **&graph, int n, int EdgeNumber)

int i = 0, a, b;
for (i = 0; i < EdgeNumber; i++)

scanf("%d %d", &a, &b); // 用户输入起点终点
AddEdge(graph[a], b); // 添加a->b的边


///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 深度优先搜索并输出
// Input: Graph - 图; n - 图的结点的个数; StartEdge — 开始的结点;
// Output: Console下输出遍历的顺序
// Tags: 递归调用 _dfs过程、回溯算法
void _dfs(Edge **&graph, bool *visited, int n, int index);
void DFS(Edge **&graph, int n, int StartEdge)

bool *visited = new bool[n]; // 标记每个结点是否已访问
memset(visited, (int)false, sizeof(bool) * n);
visited[StartEdge] = true;
printf("start edge: %d\n", StartEdge);
_dfs(graph, visited, n, StartEdge);
visited[StartEdge] = false;

// _dfs过程：
// Input: Graph - 图; n - 图的结点的个数; index - 当前的下标, visited - 记录结点是否已访问
// Output: Console下输出遍历的顺序
void _dfs(Edge **&graph, bool *visited, int n, int index)

int nIndex; // 下一个结点下标
Edge *edge = graph[index]; // 遍历用结点
while (edge) // 遍历所有的邻接结点

nIndex = edge->dest;
if (!visited[nIndex])

visited[nIndex] = true;
printf("%d\t", nIndex);
_dfs(graph, visited, n, nIndex);

edge = edge->link;



///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 广度优先搜索并输出
// Input: Graph - 图; n - 图的结点的个数; StartEdge - 开始的结点
// Output: Console下输出遍历的顺序
// Tags: 需要一个队列记录所有的灰色结点
void BFS(Edge **&graph, int n, int StartEdge)

bool *visited = new bool[n]; // 记录结点是否已访问
memset(visited, (int)false, sizeof(bool) * n);
queue<int> Q; // 记录准备访问的结点
Edge *edge; // 记录当前遍历的结点
int nIndex; // 记录下标

visited[StartEdge] = true;
printf("start edge:%d\n", StartEdge);
Q.push(StartEdge);
while (!Q.empty())

edge = graph[Q.front()];
while (edge)

nIndex = edge->dest;
if (!visited[nIndex])

visited[nIndex] = true;
printf("%d\t", nIndex);
Q.push(nIndex);

edge = edge->link;

Q.pop();


int main()

const int NODE_NUMBER = 7; // 10结点
const int EDGE_NUMBER = 11; // 10边
Edge **graph = new Edge *[NODE_NUMBER]; // 图
memset(graph, 0, sizeof(Edge *) * NODE_NUMBER); // 一开始没边
Input(graph, NODE_NUMBER, EDGE_NUMBER); // 输入边
printf("DFS:\n");
DFS(graph, NODE_NUMBER, 0); // 深度优先
printf("\n");
printf("BFS:\n");
BFS(graph, NODE_NUMBER, 0); // 广度优先
printf("\n");
return 0;


2、邻接矩阵表示的图中利用bellman-ford算法获得单点最短路
#include <cstdio>
#include <cstring>
using namespace std;
#define INTEGER_INF 0xffff // 表示无穷大路径
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 邻接矩阵表示的图
struct Graph

int **value; // 权值
int number; // 结点个数
;
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 初始化图
// Input: number - 结点个数
// Output: graph - 图
void InitGraph(Graph &graph, int number)

int i, j;
graph.value = new int *[number];
for (i = 0; i < number; i++)
graph.value[i] = new int[number];
for (i = 0; i < number; i++)

for (j = 0; j < number; j++)

if (i == j)
graph.value[i][j] = 0;
else
graph.value[i][j] = INTEGER_INF;


graph.number = number;

///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 析构图
// Input: graph - 图
// Output: graph - 析构后的图的壳子
void FreeGraph(Graph &graph)

int i;
for (i = 0; i < graph.number; i++)
delete []graph.value[i];
delete []graph.value;
graph.number = 0;

///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 用户在Console下输入图的边
// Input: n - 边的数量
// Output: graph - 加边后的图
void AddEdge(Graph &graph, int n)

int i, a, b, v;
for (i = 0; i < n; i++)

scanf("%d%d%d", &a, &b, &v);
graph.value[a][b] = v;


///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: BellmanFord 算法计算单源最短路
// Input: graph - 图, index - 起点
// Output: true - 存在最短路 且 Console 下输出起点到各个顶点的最短路
// false - 不存在最短路(存在边权和为负的环路)
bool BellmanFord(Graph &graph, int index)

int num = graph.number; // 结点个数
int *v = new int[num]; // 记录最短路
int i, j, t;
// 设定初值
for (t = 1; t < num; t++)
v[t] = INTEGER_INF;
v[index] = 0;
// 松弛
for (t = 0; t < num - 1; t++) // 循环i-1次
for (i = 0; i < num; i++)
for(j = 0; j < num; j++)
if (i != j && graph.value[i][j] != INTEGER_INF) // 如果两顶点间有路
if (v[j] > v[i] + graph.value[i][j]) // 松弛
v[j] = v[i] + graph.value[i][j];
// 判断是否存在边权和为负的环路
for (i = 0; i < num; i++)
for (j = 0; j < num; j++)
if (graph.value[i][j] != INTEGER_INF &&
v[j] > v[i] + graph.value[i][j])
return false;
// 输出
for (t = 1; t < num; t++)
printf("%d\t", v[t]);
return true;

int main()

Graph graph;
InitGraph(graph, 5);
AddEdge(graph, 10);
if (!BellmanFord(graph, 0))
printf("该图中存在边权和为负的环路!\n");
FreeGraph(graph);
return 0;
本回答被提问者和网友采纳 参考技术B ..

用c语言编写程序 输出杨辉三角

程序：

#include<stdio.h>

int main()

int n,i,j,a[100];

n=10;

printf("  1");

printf("\\n");

a[1]=a[2]=1;

printf("%3d%3d\\n",a[1],a[2]);

for(i=3;i<=n;i++)

a[1]=a[i]=1;

for(j=i-1;j>1;j--)

a[j]=a[j]+a[j-1];

for(j=1;j<=i;j++)

printf("%3d",a[j]);

printf("\\n");

return 0;

应用

与杨辉三角联系最紧密的是二项式乘方展开式的系数规律，即二项式定理。例如在杨辉三角中，第3行的三个数恰好对应着两数和的平方的展开式的每一项的系数（性质 8），第4行的四个数恰好依次对应两数和的立方的展开式的每一项的系数。

以上内容参考：百度百科-杨辉三角

参考技术A

‍#include<stdio.h>
void main()
 int i,j;
 int a[10][10]; 
 for(i=0;i<10;i++)
  a[i][0]=1;
  for(j=1;j<10;j++)
   a[0][j]=0;
  
 
 for(i=1;i<10;i++)
  for(j=1;j<10;j++) 
   a[i][j]=a[i-1][j-1]+a[i-1][j];
  
 
 for(i=0;i<10;i++)
  for(j=0;j<=i;j++) 
   
   printf("%4d",a[i][j]); 
   if(j==i)printf("\\n\\n");
  
 

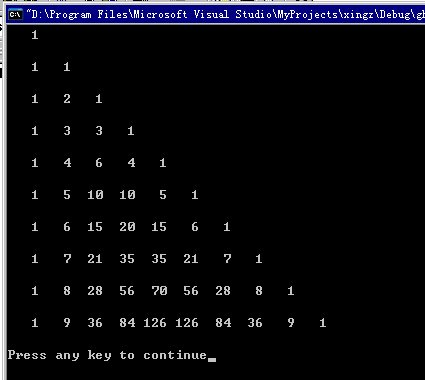
希望可以帮到你！望采纳！

本回答被提问者和网友采纳 参考技术B #include<stdio.h>int main() int i,j; int a[10][10]; printf("\n"); for(i=0;i<10;i++) a[i][0]=1; a[i][i]=1; for(i=2;i<10;i++) for(j=1;j<i;j++) a[i][j]=a[i-1][j-1]+a[i-1][j]; for(i=9;i>=0;i--) for(j=0;j<=i;j++) printf("%5d",a[i][j]); printf("\n"); return 0;
希望能解决您的问题。追问

很多错勒