求二叉树中从根结点到叶子节点的路径

Posted 2023-05-02

对于二叉树，分别用递归和非递归的方法编写程序完成如下功能：
1． 输出所有的叶子结点的数据项值。
2． 输出所有从叶子节点到根结点的路径
3． 输出（2）中的第一条最长的路径

b=NULL;     //建立的二叉树初始时为空

ch=str[j];

while(ch!='\\0')    //str未扫描完时循环

switch(ch)

case '(':top++;St[top]=p;k=1;break;     //为左结点

case ')':top--;break;

case ',':k=2;break;     //为右结点

default :p=(BTNode *)malloc(sizeof(BTNode));

p->data=ch;

p->lchild=p->rchild=NULL;

if(b==NULL)

b=p; //p指向二叉树的根结点

else

switch(k)

case 1:St[top]->lchild=p;break;

case 2:St[top]->rchild=p;break;

int main()

BTNode *b;

ElemType path[MaxSize],longpath[MaxSize];

int i,longpathlen=0;

CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");

printf("二叉树b:");DispBTNode(b);printf("\\n\\n");

printf("b的叶子结点：");DispLeaf(b);printf("\\n\\n");

printf("AllPath:\\n");AllPath(b);printf("\\n");

printf("AllPath1:\\n");AllPath1(b,path,0);printf("\\n");

LongPath(b,path,0,longpath,longpathlen);

printf("第一条最长路径长度：%d\\n",longpathlen);

printf("第一条最长路径：");

for(i=longpathlen;i>=0;i--)

printf("%c ",longpath[i]);

printf("\\n");

return 0;

扩展资料；

遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。

设L、D、R分别表示遍历左子树、访问根结点和遍历右子树， 则对一棵二叉树的遍历有三种情况：DLR（称为先根次序遍历），LDR（称为中根次序遍历），LRD （称为后根次序遍历）。

参考资料来源：百度百科-二叉树

参考技术A #include<stdio.h>
#include<malloc.h>
#define MaxSize 100
typedef char ElemType;
typedef struct node
    ElemType data;      //数据元素
    struct node *lchild;    //指向左孩子
    struct node *rchild;    //指向右孩子
BTNode;
void CreateBTNode(BTNode *&b,char *str)    //由str串创建二叉链
    BTNode *St[MaxSize],*p=NULL;
    int top=-1,k,j=0;
    char ch;
    b=NULL;     //建立的二叉树初始时为空
    ch=str[j];
    while(ch!='\\0')    //str未扫描完时循环
        switch(ch)
            case '(':top++;St[top]=p;k=1;break;     //为左结点
            case ')':top--;break;
            case ',':k=2;break;     //为右结点
            default :p=(BTNode *)malloc(sizeof(BTNode));
                    p->data=ch;
                    p->lchild=p->rchild=NULL;
                    if(b==NULL)
                        b=p;        //p指向二叉树的根结点
                    else
                        switch(k)
                            case 1:St[top]->lchild=p;break;
                            case 2:St[top]->rchild=p;break;
                        
                    
        
        j++;
        ch=str[j];
    

void DispBTNode(BTNode *b)     //以括号表示法输出二叉树
    if(b!=NULL)
        printf("%c",b->data);
        if(b->lchild!=NULL || b->rchild!=NULL)
            printf("(");
            DispBTNode(b->lchild);
            if(b->rchild!=NULL)
                printf(",");
            DispBTNode(b->rchild);
            printf(")");
        
    

void AllPath(BTNode *b)        //采用非递归方法输出从叶子结点到根结点的路径
    struct snode
        BTNode *node;   //存放当前结点指针
        int parent;     //存放双亲结点在队列中的位置
    Qu[MaxSize];   //定义顺序队列
    int front,rear,p;       //定义队头和队尾指针
    front=rear=-1;      //置队列为空队列
    rear++;
    Qu[rear].node=b;        //根结点指针进入队列
    Qu[rear].parent=-1;     //根结点没有双亲结点
    while(front<rear)      //队列不为空
        front++;
        b=Qu[front].node;       //队头出队列
        if(b->lchild==NULL && b->rchild==NULL) //*b为叶子结点
            printf("%c到根结点路径：",b->data);
            p=front;
            while(Qu[p].parent!=-1)
                printf("%c ",Qu[p].node->data);
                p=Qu[p].parent;
            
            printf("%c\\n",Qu[p].node->data);
        
        if(b->lchild!=NULL)    //左孩子入队列
            rear++;
            Qu[rear].node=b->lchild;
            Qu[rear].parent=front;
        
        if(b->rchild!=NULL)    //右孩子入队列
            rear++;
            Qu[rear].node=b->rchild;
            Qu[rear].parent=front;
        
    

void AllPath1(BTNode *b,ElemType path[],int pathlen)   //采用递归方法输出从叶子结点到根结点的路径
    int i;
    if(b!=NULL)
        if(b->lchild==NULL && b->rchild==NULL) //*b为叶子结点
            printf("%c到根结点路径：%c ",b->data,b->data);
            for(i=pathlen-1;i>=0;i--)
                printf("%c ",path[i]);
            printf("\\n");
        else
            path[pathlen]=b->data;  //将当前结点放入路径中
            pathlen++;
            AllPath1(b->lchild,path,pathlen);   //递归扫描左子树
            AllPath1(b->rchild,path,pathlen);   //递归扫描右子树
            pathlen--;
        
    

void LongPath(BTNode *b,ElemType path[],int pathlen,ElemType longpath[],int &longpathlen)  //求最长路径
    int i;
    if(b==NULL)
        if(pathlen>longpathlen)    //若当前路径更长，将路径保存在longpath中
            for(i=pathlen-1;i>=0;i--)
                longpath[i]=path[i];
            longpathlen=pathlen;
        
    else
        path[pathlen]=b->data;      //将当前结点放入路径中
        pathlen++;      //路径长度增1
        LongPath(b->lchild,path,pathlen,longpath,longpathlen);  //递归扫描左子树
        LongPath(b->rchild,path,pathlen,longpath,longpathlen);  //递归扫描右子树
        pathlen--;      //恢复环境
    

void DispLeaf(BTNode *b)   //输出叶子结点
    if(b!=NULL)
        if(b->lchild==NULL && b->rchild==NULL)
            printf("%c ",b->data);
        else
            DispLeaf(b->lchild);
            DispLeaf(b->rchild);
        
    

int main()
    BTNode *b;
    ElemType path[MaxSize],longpath[MaxSize];
    int i,longpathlen=0;
    CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
    printf("二叉树b:");DispBTNode(b);printf("\\n\\n");
    printf("b的叶子结点：");DispLeaf(b);printf("\\n\\n");
    printf("AllPath:\\n");AllPath(b);printf("\\n");
    printf("AllPath1:\\n");AllPath1(b,path,0);printf("\\n");
    LongPath(b,path,0,longpath,longpathlen);
    printf("第一条最长路径长度：%d\\n",longpathlen);
    printf("第一条最长路径：");
    for(i=longpathlen;i>=0;i--)
        printf("%c ",longpath[i]);
    printf("\\n");
    return 0;

二叉树

树的基本术语：

度：结点拥有的子树数。度为0的结点称为叶子或终端结点。度不为0的结点称为分支结点。树的度是指树内各结点的度的最大值。

树的层次：从根开始，根为第一层。树中结点的最大层次称为树的深度或高度。

树的深度和高度是相等的，而对其他节点来说深度和高度不一定相等。

某节点的深度是指从根节点到该节点的最长简单路径边的条数，而高度是指从该节点到叶子节点的最长简单路径边的条数。深度上往下，高度下往上

二叉树性质：

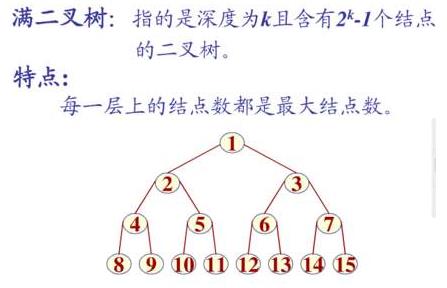
1.一个有k层的二叉树总结点最多有2^k-1个；（满二叉树情况）

2.叶子结点最多有2^k-1个；（满二叉树）

3.总结点个数

s = n0+n1+n2;

s = n0*0+n1*1+n2*2+1; 由上两式-> n0 = n2+1;

对完全二叉树（除了最后一层其他都满，最后一层结点依次左往右排没有空缺），n1 = 0 或1个；有下列两个性质

4.n个结点的完全二叉树高度k =  ⌊log₂ n⌋ +1（向下取整）；包含n个节点的二叉树的高度至少为log₂(n+1)。

5.标记0~n-1;

左子树:2i+1 <= n-1；

右子树：2i+2  <= n-1;

父亲结点范围 0~n/2-1

二叉树的遍历，深度和广度

深度：前序（根左右）中序（左根右）后序（左右根）

广度：层序遍历。先来先处理

对深度和广度两种遍历分别可以使用栈和队列来实现（非递归实现遍历）

代码待更新