深入理解一趟冒泡排序的本质，解决二维数组中求子数组最大和

Posted 2021-04-07 算法与数据结构面试辅导

gaominginterview

加关注

深入理解一趟冒泡排序的本质

场景回顾

在一个大矩阵中求一个最大的二维矩阵。其实就是在一个二维数组中找到一个X, Y使得（X,Y）,(X, Y+1),(X+1, Y),(X+1, Y+1) 组成的和比其他的任何类似的子数组都大。

这里有一个例子， 在矩阵中：

1 2 0 3 4

2 3 4 5 1
1 1 5 3 0
中最大的二维矩阵是:
4 5

5 3

好了，大家理解了大矩阵的其实就是一个二维数组，而二维矩阵其实就是由点 （X,Y）向右、向下构成的四个点的子数组。没毛病对吗？ 看下这张图，你会更加直观。

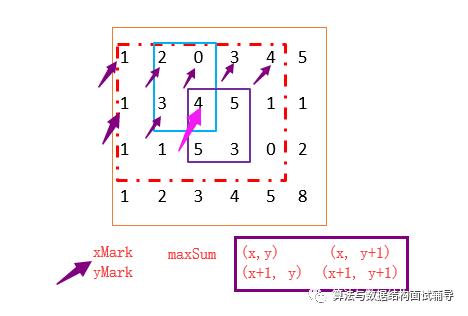
分析问题

1. 紫色红色块部分是最大的和，

2. 蓝色块也会构成四个数的和，不是最大的，

3. 这样的X，Y其实就限定在红色区域里

解题思路

那怎么解决这样一道问题呢？我们分析下两个思路，之后我们再挖掘下题目的本质：

1. 我们把每个点（X, Y）以及由 该点出发构成的四个点的和都求出来，之后我们再扫描下结构，找最大的数。我们是不是就可以求出来了呢？

   
   

   如果是这样的话，我们可以构造一个一维数组就好了，这个数组中保存的就是由（X,Y）点出发而构成的四个数的和。而我们可以从下表中求出（X，Y），我们用i来表示下标，则有  x = i / 数组的第二维长度, Y = i - X * 数组的第二位长度。需要注意的是， 此时 X的最大值等于 数组的一唯长度 - 2， 而Y 的最大值等于数组的二维长度 -2；

2. 大家看明白了第一种思路之后，是不是可以再做一些优化。我们真的需要把每个长度都求出来吗？

问题的本质是什么？

一趟冒泡，求最大值！！！

该题的本质，其实就是一趟冒泡排序，找出最大值。对不对？

这是思路1 的本质。在思路2中我们同样使用这样的思路，只是更加深刻的理解它，我们只需两两比较，每次保存最大的值作为哨兵就好了。不太理解的同学建议查看原文系统学习排序专题。

一起写代码

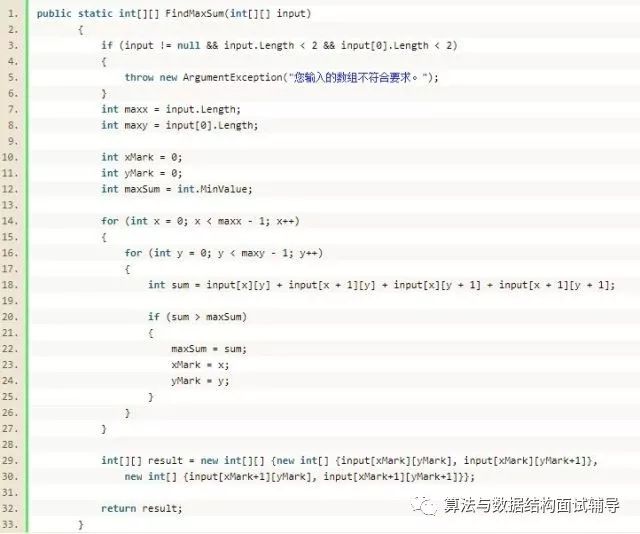
测试结果

最后希望大家在学习的数据结构与算法的道路上越走越远，越来越顺畅。

查看原文

获取更多专题课程

点击“阅读原文”打开新页面