从冒泡排序到快速排序,我总结了这几点
Posted 算法刷题日记
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从冒泡排序到快速排序,我总结了这几点相关的知识,希望对你有一定的参考价值。
▼ ▼ ▼ ▼ ▼ ▼ ▼ ▼ ▼
01
—
你会学到什么?
彻底弄明白常用的排序算法的基本思想,算法的时间和空间复杂度,以及如何选择这些排序算法,确定要解决的问题的最佳排序算法,我们先总结下冒泡排序和其改进后的快速排序这两个算法,后面再继续总结插入排序、希尔排序、选择排序、堆排序、归并排序和基数排序。
02
—
讨论的问题是什么?
各种排序算法的基本思想;讨论各种排序算法的时间、空间复杂度;以及算法的稳定性;算法是如何改进的,比如冒泡排序如何改进成了目前最常用的快速排序的。
03
—
相关的概念和理论
内部排序
若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
外部排序
若参加排序的记录数量很大,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
就地排序
若排序算法所需的辅助空间并不依赖于问题的规模n,即辅助空间为O(1),称为就地排序。
稳定排序
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序后,这些记录的相对次序保持不变,即在原序列中 ri=rj, ri 在 rj 之前,而在排序后的序列中,ri 仍在 rj 之前,则称这种排序算法是稳定的;否则称为不稳定的。
排序序列分布
排序需要考虑待排序关键字的分布情况,这会影响对排序算法的选择,通常我们在分析下列算法时都考虑关键字分布是随机分布的,不是按照某种规律分布的,比如正态分布等。
待排序序列
排序序列中,剩余即将要排序的序列部分。
已排序序列
排序序列中,已经排序好的序列部分。
04
—
两两比较的冒泡排序
冒泡排序思想
英文名称是 bubble sort
已知一组无序数据a[0]、a[1]、……a[n-1],需将其用冒泡排序按升序排列。
首先比较a[0]与a[1]的值,若a[0]大于a[1]则交换两者的值,否则不变。再比较a[1]与a[2]的值,若a[1]大于a[2],则交换两者的值,否则不变。以此类推。。。最后比较a[n-2]与a[n-1]的值。这样处理一轮后,a[n-1]的值一定是这组数据中最大的。
再对a[0]~a[n-2]以相同方法处理一轮,则a[n-2]的值一定是a[0]~a[n-2]中最大的。以此类推。。。
这样共处理 n-1 轮后a[0]、a[1]、……a[n-1]就以升序排列了。
升序排序的例子
待排序列 3 2 5 9 2
第一轮
第1次比较 2 3 5 9 2
第2次比较 2 3 5 9 2
第3次比较 2 3 5 9 2
第4次比较 2 3 5 2 | 9
第二轮
第5次比较 2 3 5 2 9
第6次比较 2 3 5 2 9
第7次比较 2 3 2 | 5 9
第三轮
第8次比较 2 3 2 5 9
第9次比较 2 2 | 3 5 9
第四轮
第10次比较 2 | 2 3 5 9
以上分割线左侧为下一轮的待排序序列,右侧为已排序好的序列。
可以看到5个关键码组成的序列,经过4轮共计10次比较,比较次数是不变的,比较次数公式为:
n * (n-1) / 2
算法评价
优点:如果你不是故意去交换相等的关键码的话,这个算法是绝对稳定的排序算法。
缺点:比较次数也就是所谓的时间复杂度 为O(n^2),最好的情况和最坏的情况都是O(n^2)。
从上面例子中,我们可以看到第一、二、三轮,2和3两个关键码重复比较了3次,很显然这不是令人满意的,那么如何解决这个问题呢?答案是快速排序,请看下节。
05
—
改进后的快速排序算法
快速排序(Quicksort)是对冒泡排序的一种改进。
快速排序由 Hoare 在1962年提出,以下是这位计算机科学家的大头照,是一位和蔼可亲的老头,哎,还是个秃子,不过对搞计算机的人来说,这并不足为奇!
快速排序的基本思想
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小。
然后再按此方法对这其中一部分数据进行快速排序,这是递归调用。
再按此方法对另一部分数据进行快速排序,这也是递归调用。
算法介绍
设要排序的数组是A[0]……A[n-1]
首先任意选取一个数据作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。
一趟快速排序算法
设置两个变量 i、j,排序开始的时候:i=0,j=n-1;
以第一个数组元素作为关键数据,赋值给 pivot,即 pivot =A[0];
从 j 开始向前搜索,即由后开始向前搜索(j--),找到第一个小于 pivot 的值A[j],将 A[j] 和 A[i] 互换(互换保证了 A[j] < A[i],也就是保证了要趋向于前方的关键码都小于 pivot );
从 i 开始向后搜索,即由前开始向后搜索(i++),找到第一个大于pivot 的A[i],将 A[i] 和 A[j] 互换(互换保证了 A[j] < A[i],也就是保证了后方的关键码都大于 pivot )
重复第3、4步,直到 i=j 。
完成本轮比较
快速排序例子
我们仍然以冒泡排序举的那个例子来模拟演示快速排序,待排序的序列为:
3 2 5 9 2
第一轮比较,选取第一个关键码 3 为pivot,初始值 i =0, j =4,如下图圈1所示,
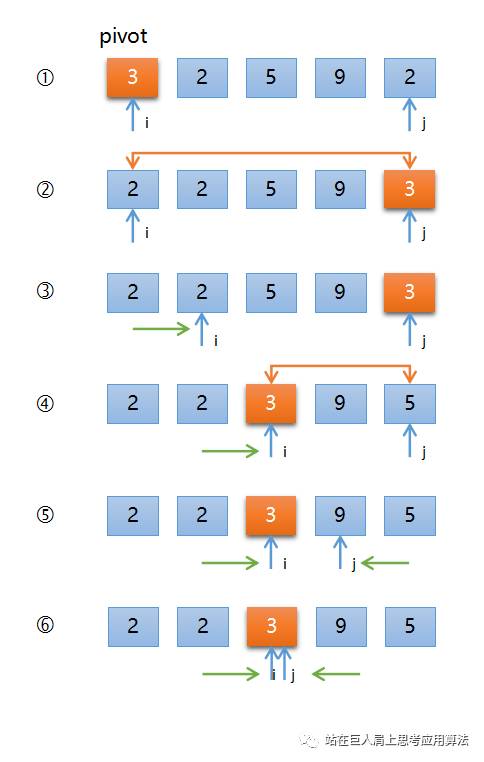
A[j]=5与pivot比较,因为后面的关键码2小,所以要与pivot交换,如圈2所示,大家注意看下,经过这一步操作,原来靠后的关键码2跑到了原先靠前的关键码2前方,所以快速排序不是稳定的排序算法(稳定排序的概念请见第03节的说明)。
该到移动 i 的时候了,等到圈4的时候,关键码 5大于pivot,需要交换,让5放在pivot的后面,因为pivot后面的要比它大吗,如圈4所示。
该到移动 j 的时候了,关键码9显然大于pivot,如圈5所示,所以 j 继续向前移动。
j此时已经与i重合了,所以while循环终止,至此完成了第一轮迭代。
可以看到pivot位置的变动,刚开始位于索引0处,然后又到最后位置,最后定格在索引2处。我们很幸运的是,经过本轮快排后,pivot=3把排序区间划分的比较均匀,前面有2个元素,后面也有2个元素,这是理想的!后面,我们在分析快排的性能时会意识到这个幸运的重要性!
完成了第一轮迭代后,再就是对pivot前的区间再次执行上述操作,然后再对pivot后的区间也是执行上述操作。
整个快速排序完成。
快排和冒泡的直观比较
上面这个例子,快速排序第一轮经过了5次比较,2次交换,使得Pivot将整个排序序列分割成两个独立的区间,前面都小于Pivot,后面都大于Pivot;前面区间只需要1次比较,0次交换即可完成;后面区间只需要1次比较,1次交换就可完成,因此总的比较次数为7次,交换次数为3次。
而同样冒泡排序呢,由上节我们知道它需要10次比较,4次交换才能完成排序。
06
—
快速排序算法评价
最坏情况
快速排序的最坏情况,实际上就退化为了冒泡排序的情况,想想冒泡排序,每一轮比较后,都将原来的排序好的区间增加了一个长度,也就是说快速排序每次选择的pivot也正好达成了冒泡排序的作用,那么最坏情况就此发生。简单来说,最坏情况发生在每次划分过程产生的两个区间分别包含n-1个元素和1个元素的时候。那么不难知道,最坏情况的复杂度也为 O(n^2)。
最好情况
如果每次划分过程产生的区间大小都为n/2,则快速排序法运行就快得多了,此时的时间复杂度为 O(nlogn),logn表示以2为底,n的对数。因为每轮比较都会平均分成2个区间,共经过趋向于n轮的比较。
平均情况
平均情况和最好情况的时间复杂度都为O(nlogn),只不过平均情况的常数因子可能大一些,有关详细分析,请查阅相关资料。
快速排序的再改进
快速排序的再改进,可从分区策略上优化,在此我们不做详细介绍,有兴趣可查看相关资料,有可能的话,接下来,再对这个话题单独写一篇。
07
—
总结
冒泡排序是两两比较的算法,一轮下来,找到一个最值,比较次数是固定的,时间复杂为 O(n^2);
而快速排序改进了冒泡排序,每轮比较都选取一个pivot,每轮比较后pivot将待排序序列分为2个部分,前面部分都小于pivot,后面都大于pivot,这种改进,在不出现最坏情况下,直接提升了排序的时间复杂度,因为相当于一轮比较将排序序列一分为二,使得快排的时间复杂度在平均意义上为O(nlogn);
不过,快排的最坏复杂度即退化为冒泡排序时,时间复杂度为O(n^2),比如一种待排序的序列已经为升序序列,那么每轮分割区间长度为1,n-1,不就是退化为了冒泡排序了吗。在实际操作中,有很多技术可以降低最坏情况发生的概率,快速排序克服了这个问题后,使得自己应用很广泛。
更多其他排序算法,请关注接下来的消息推送,谢谢。
▼ ▼ ▼ ▼ ▼ ▼
以上是关于从冒泡排序到快速排序,我总结了这几点的主要内容,如果未能解决你的问题,请参考以下文章