特么，冒泡排序有这么难？

Posted 2021-04-07 景禹

冒泡排序乍看最为简单，但请你问自己下面几个问题：

1. 冒泡排序如何判断数组是否有序了呢？
2. 冒泡排序数组 [3,1,2,4,5,6,7,8,9] 是否有优化方式呢？
3. 冒泡排序最好的时间复杂度，最坏的时间复杂度，还有空间复杂度清楚吗？
4. 如何用递归的形式实现冒泡排序？
5. 如何使用两个栈来实现冒泡排序？
6. 对单链表又该如何进行冒泡排序？
7. 最后一个简单的，如何使用冒泡排序对字符串数组进行排序？

如果你看着每一个问题，心中都很明朗，就此打住；若不是，希望你从这篇文章中收获到你想要的东西，也会对这些问题进行分析和讲解。

还有制作动画的福利奥~

冒泡排序

冒泡排序是最简单的排序算法了，简单到景禹不知如何更清晰地呈现（哈哈，开个玩笑）。冒泡排序通过不断地比较两个相邻元素，将较大的元素交换到右边（升序），从而实现排序。

话不多说，上例子：

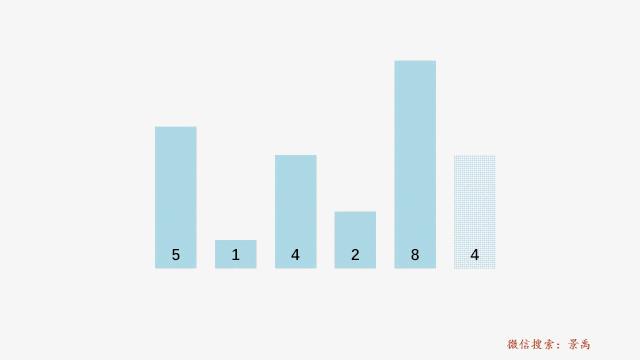
我们对数组 [5，1，4，2，8，4] ，采用冒泡排序进行排序，注意这里的两个 4 的纹理是不同的，主要是为了区分两个不同的 4 ，进而解释冒泡排序算法的稳定性问题。

第一轮冒泡排序

第一步：比较 5 和 1 ，5 > 1，则交换 5 和 1 的位置：

比较大小：

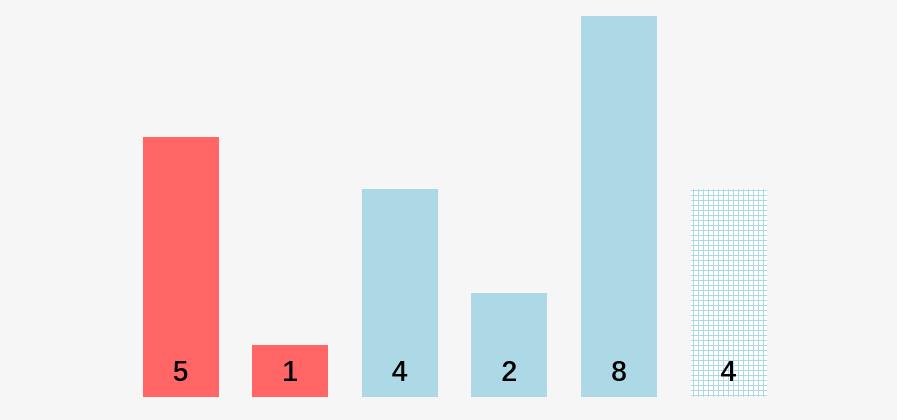
交换位置：

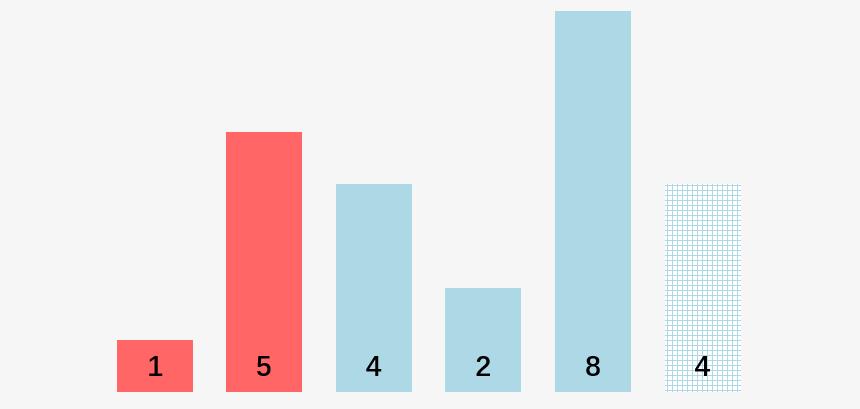
第二步，比较 5 和 4，5 > 4，交换 5 和 4 的位置：

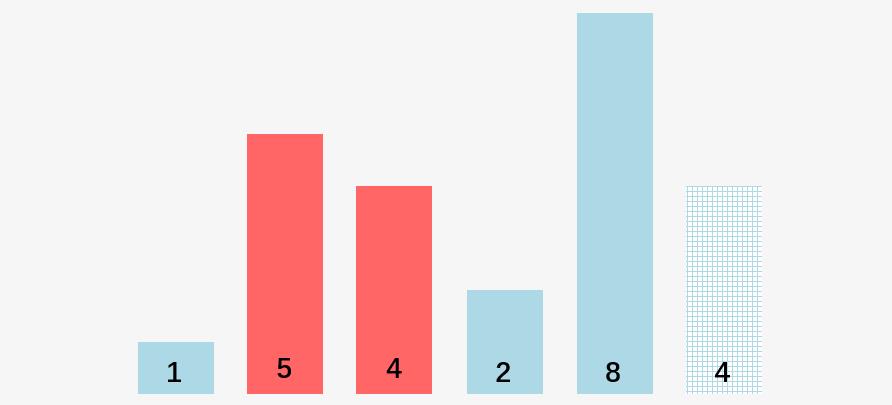
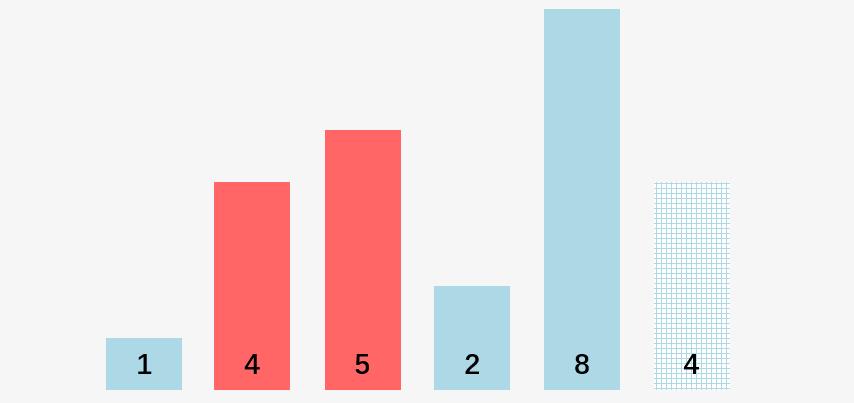
第三步：比较 5 和 2 ，5 > 2，交换 5 和 2 的位置：

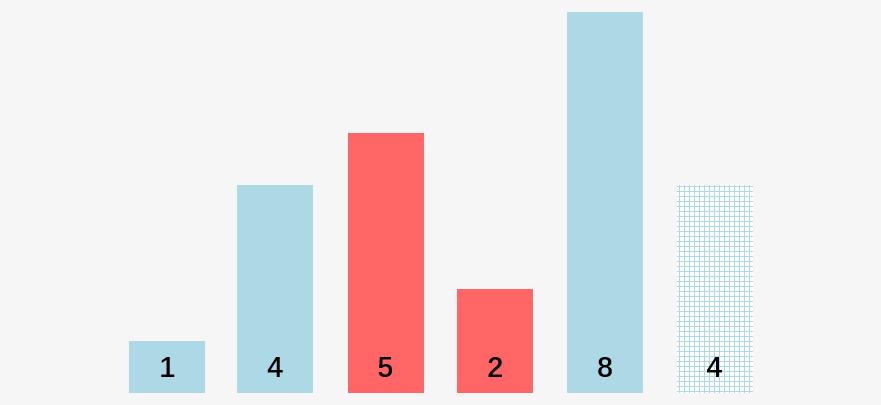
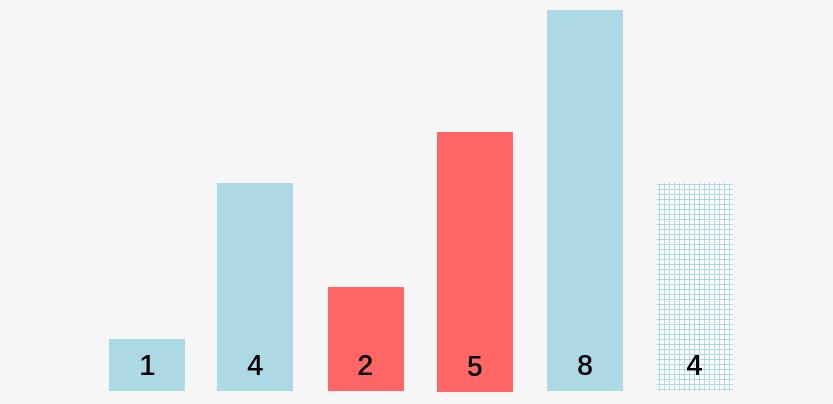
第四步：比较 5 和 8 ，5 < 8 ，不交换

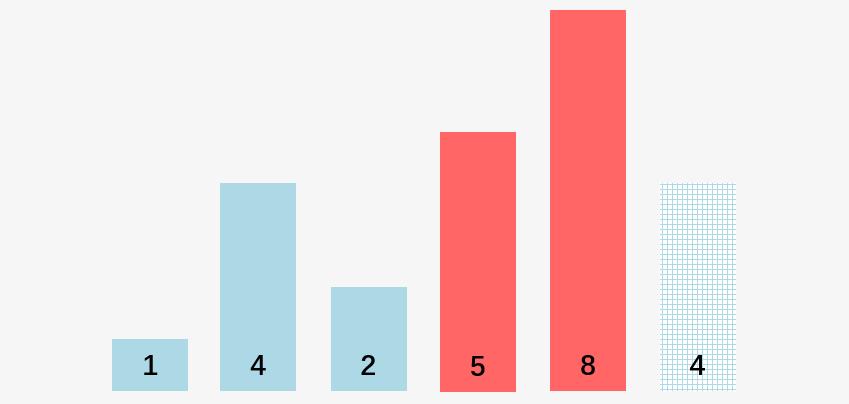
第五步：比较 8 和 4 ， 8 > 4，交换 8 和 4 ：

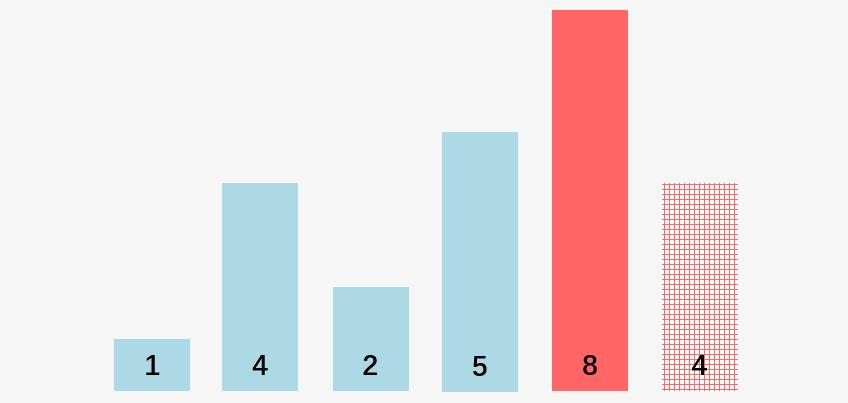
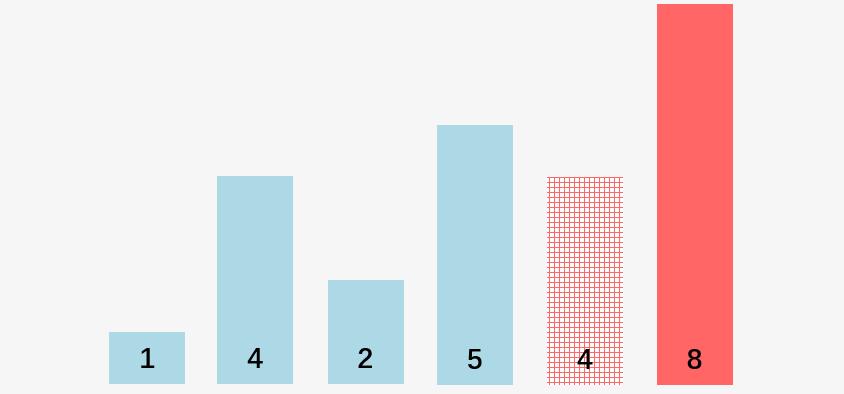
此刻我们获得数组当中最大的元素 8 ，使用橘黄色进行标记：

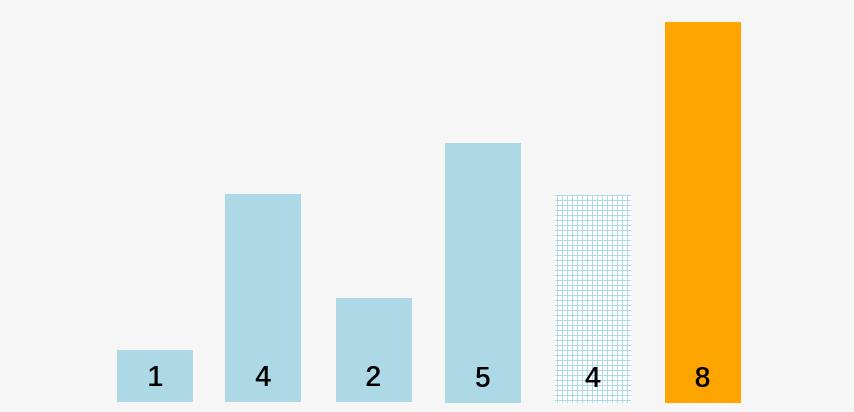
景禹写的图文中的动画如何制作？（插曲）

上面给各位盆友讲冒泡排序的 11 张图都是景禹在 PowerPoint （俗称PPT）中一张一张画的，不信你看：

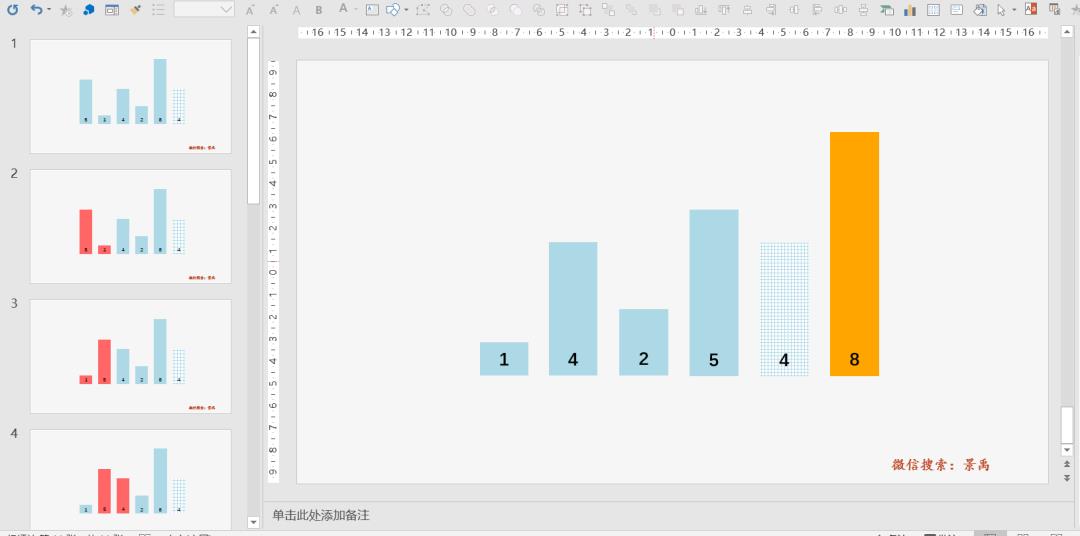
具体如何绘制，我就不给大家教学了，矩形框，文本框等等之类，大家在网上稍微学一下就能够学会。关键是有了这 11 张图如何制作一个 GIF动图呢？

首先要把 PPT 中的每一页都保存成 jpg 或者 png 格式的图片，然后打开 Easy GIF Animator 点击 创建新的动画  :

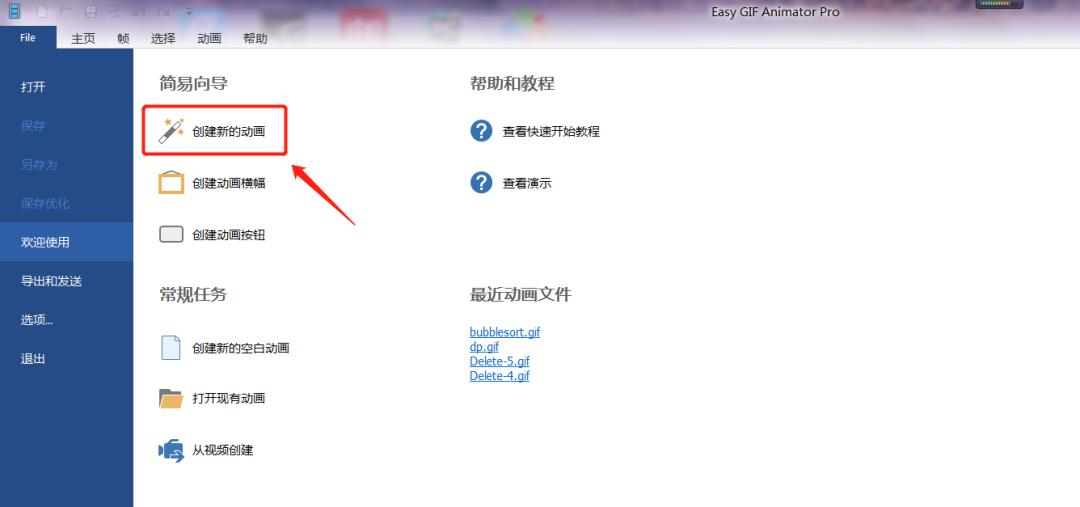
然后点击 添加图像 ，将 PPT 中保存的 11 张图片添加进来：

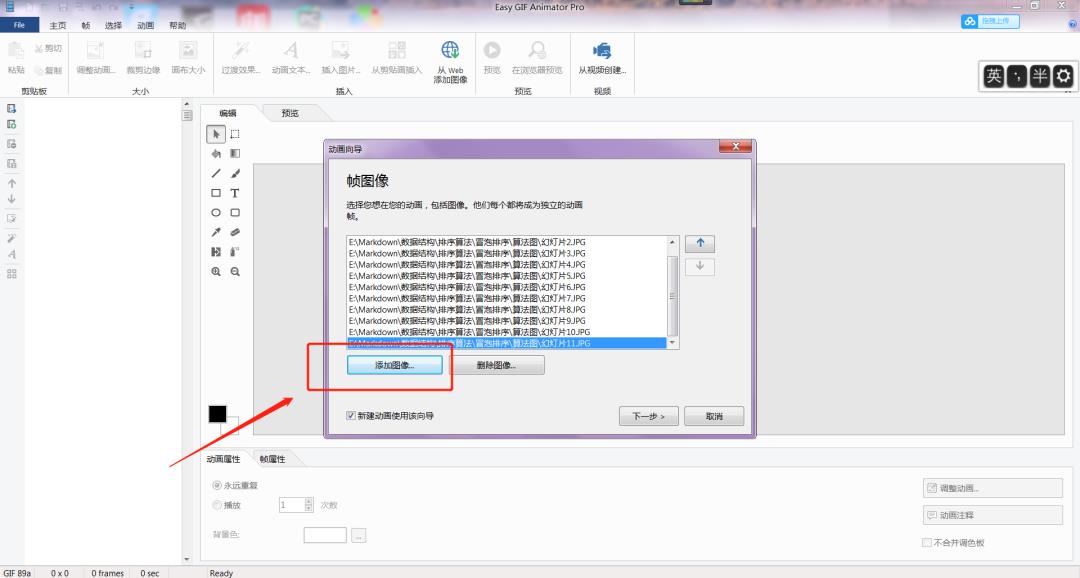
然后下一步，会看到下面的向导：

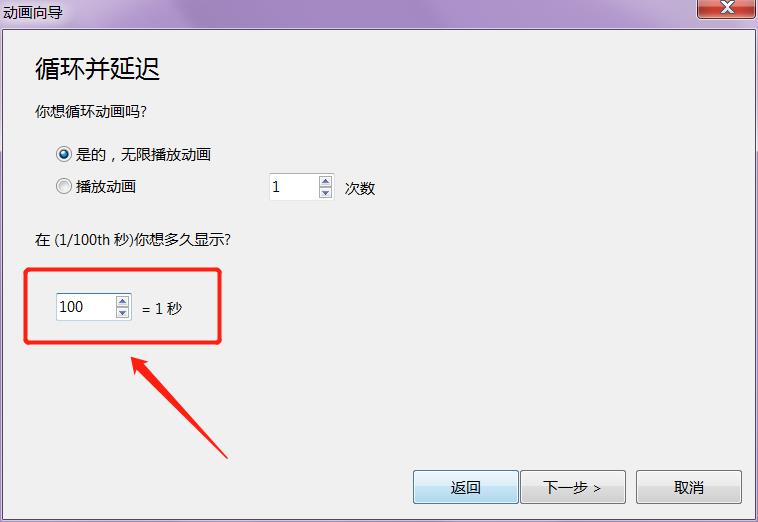
通常景禹是将这个切换速度改为 100，也就是 1秒，之后就是下一步，下一步，完成。

然后保存成 gif 就可以了，如下所示。

第一轮冒泡动画演示

第二轮冒泡动画演示

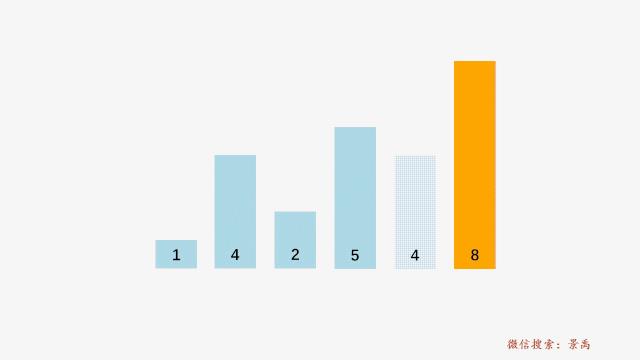
事实上第二阶段结束，整个数组已经有序了，但是对于冒泡排序而言并不知道，她还需要通过第三阶段的比较操作进行判断。

第三轮冒泡动画演示

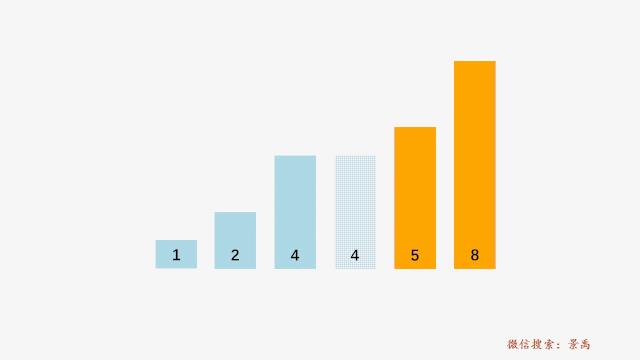
对于冒泡排序算法而言，她是通过判断整个第三阶段的比较过程中是否发生了交换来确定数组是否有序的，显然上面的过程中没有交换操作，冒泡排序也就知道了数组有序，整个算法执行结束。

冒泡排序的实现

不考虑优化的实现方式

void swap(int *xp, int *yp) 
{ 
 int temp = *xp; 
 *xp = *yp; 
 *yp = temp; 
} 

// 冒泡排序 
void bubbleSort(int arr[], int n) 
{ 
    int i, j; 
    for (i = 0; i < n-1; i++)  

        // 每一次找出一个元素的合适位置。
        for (j = 0; j < n-i-1; j++) 
            if (arr[j] > arr[j+1]) 
                swap(&arr[j], &arr[j+1]); 
} 

这种实现方式有一个明显的弊端，就是不论数组是否有序，两层 for 循环都要执行一遍，而聪明的小禹希望数组有序的时候，仅进行一轮判断，或者一轮都不进行（当然不判断，排序算法是不能知道数组是否有序的）。所以我们一起来看看数组有序的情况下，仅判断一轮的情况如何实现。

一次优化的实现方式

void swap(int *xp, int *yp) 
{ 
 int temp = *xp; 
 *xp = *yp; 
 *yp = temp; 
} 

// 冒泡排序的优化版本
void bubbleSort(int arr[], int n) 
{ 
    int i, j; 
    bool swapped; //用于标记数组是否有序
    for (i = 0; i < n-1; i++) 
    { 
        swapped = false; //初始化为 false
        for (j = 0; j < n-i-1; j++) 
        { 
            if (arr[j] > arr[j+1]) 
            { 
                swap(&arr[j], &arr[j+1]); 
                swapped = true; 
            } 
        } 

        // 如果swapped 为 false ,说明没有交换，数组有序，退出排序 
        if (swapped == false) 
            break; 
    } 
} 

这里我们增加了一个标识数组是否有序的布尔变量 swapped ，当冒泡排序过程中没有交换操作时，swapped = false ，也意味着数组有序；否则数组无序继续进行冒泡排序。不要小看这个变量奥，因为这个变量，当数组有序的时候，冒泡排序的时间复杂度将降至 (因为其只需要执行一遍内层的 for 循环就可以结束冒泡排序)，没有这个变量，数组有序也需要 的时间复杂度。

二次优化的实现方式

一次优化是为了避免数组有序的情况下，继续进行判断操作的。那么二次优化又为了什么呢？

我们看下面的例子。

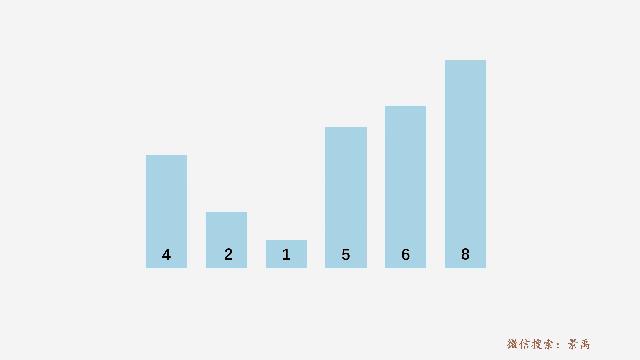
输入数组：

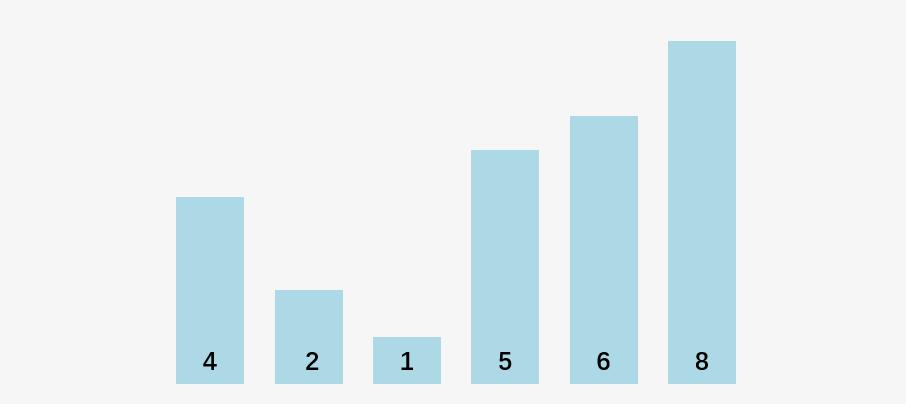
一次优化的冒泡排序执行动画演示：

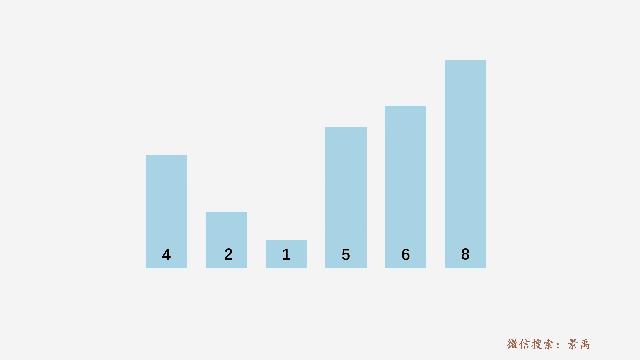
但是我们注意到，数组数组中的 [5,6,8] 本身已经有序，而对于有序的部分进行比较是没有意义的，相当于在白白浪费资源，有没有什么办法减少这样的比较次数呢？

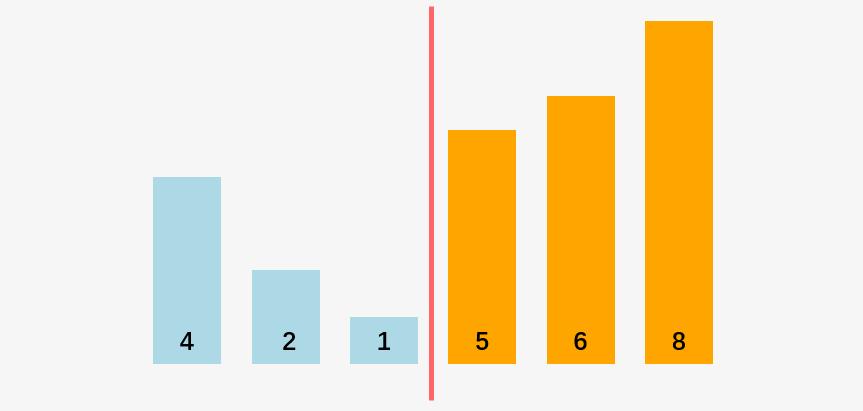
换句话说，是否能够确定出已经有序部分和无序部分的边界呢？

答案当然是肯定的，这个边界就是第一趟冒泡排序的过程中最后一次发生交换的位置 j ：

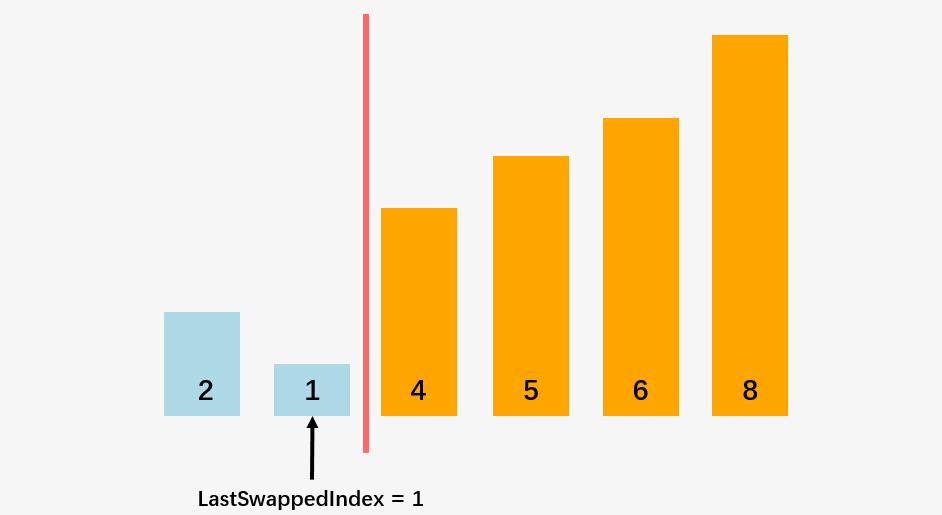
也就是 1 和 4 发生交换之后，4 和 5 没有发生交换，此时 1 之后的元素为有序。

还不清晰，我们分步骤看一下：

第一步：4 和 2比较，4 > 2 ，交换 4 和 2 ，将  LastSwappedIndex = 0；

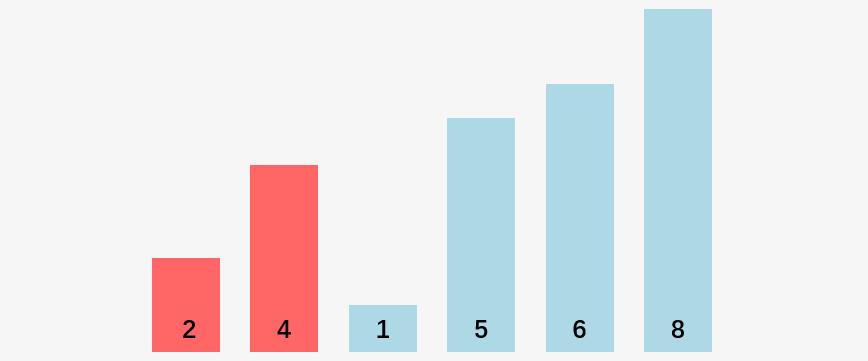
第二步：4 和 1 比较，4 > 1，交换 4 和 1，  LastSwappedIndex = 1 ；

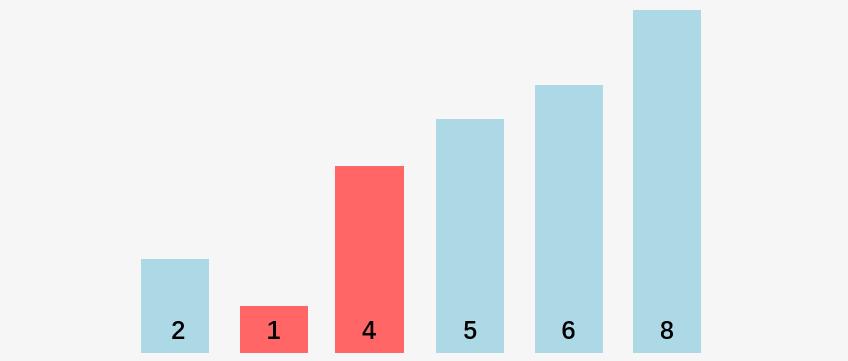
第三步：比较 4 和 5 ， 4 < 5，不交换， lastSwappedIndex 也不更新;

第四步：比较 5 和 6 ，不交换， lastSwappedIndex 也不更新;

第五步：比较 6 和 8 ，不交换， lastSwappedIndex 也不更新;

第一趟冒泡排序结束了，这里似乎看不出和之前有什么区别，但是来看第二趟冒泡排序就不一样了，此时 j 的 取值将从 j = 0 到 j = lastSwappedIndex ，

第一步：比较 2 和 1 ，2 > 1，交换，lastSwappedIndex = 0 ，并且第二趟冒泡也就结束了，也就说我们节省了 从 2 到 6的比较操作；

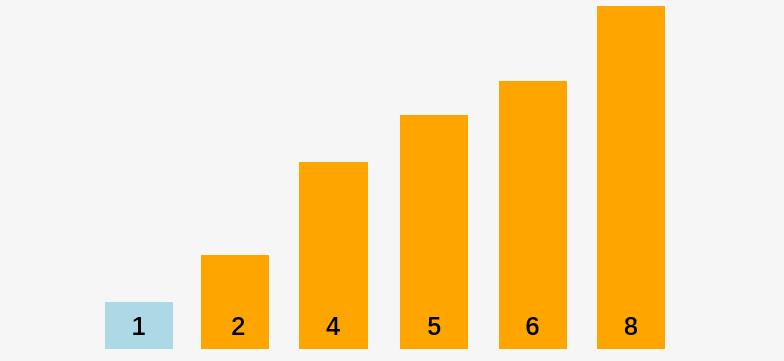
最后再来一趟冒泡排序，发现没有任何交换，所以冒泡排序结束。

相比于一次优化的实现方式，二次优化的实现方式进一步减少了不必要的执行次数，两种优化后的实现方式需要冒泡排序的趟数是一样的，本质上没有什么区别。所以即使对于一个有序的数组，两种方式的时间复杂度都是 .

动画演示：

实现代码：

void swap(int *xp, int *yp) 
{ 
 int temp = *xp; 
 *xp = *yp; 
 *yp = temp; 
} 

// 冒泡排序的优化版本
void bubbleSort(int arr[], int n) 
{ 
    int i, j; 
    bool swapped; //用于标记数组是否有序
    int lastSwappedIndex = 0; //记录最后一次交换的位置
    int sortBorder = array.length - 1; //将有序和无序部分的边界初始化为最后一个元素
    for (i = 0; i < n-1; i++) 
    { 
        swapped = false; //初始化为 false
        for (j = 0; j < sortBorder; j++) 
        { 
            if (arr[j] > arr[j+1]) 
            { 
                swap(&arr[j], &arr[j+1]); 
                swapped = true; 
                lastSwappedIndex = j;
            } 
        } 
  sortBorder = lastSwappedIndex;
        // 如果swapped 为 false ,说明没有交换，数组有序，退出排序 
        if (swapped == false) 
            break; 
    } 
} 

复杂度分析

时间复杂度

最坏情况下（数组逆序）：

当 i == 0 的时候，j 的取值范围是从 0 到 n -1，内循环的执行判断和交换操作 n - 1 次；

当 i == 1 的时候，j 的取值范围是从 0 到 n -2，内循环的执行判断和交换操作 n - 2 次；

以此类推......

当 i 取最大值 n - 2 时，j 的取值为 1，内循环的执行判断操作 1 次；

所以，整体内循环的判断语句执行次数就是：1 + 2 + 3 + ... + (n - 2) + (n - 1) 。

则最坏情况下的时间复杂度为 量级。

最好情况下（数组有序）：

当 i == 0 的时候，swapped = false ，j 的取值范围是从 0 到 n -1，内循环的执行判断操作 n - 1 次，但是没有发生交换操作，冒泡排序算法直到数组已经有序，所以执行结束。

则最好情况下的时间复杂度为

空间复杂度

冒泡排序没有使用任何额外的空间，空间复杂度为 ，是典型的 原地排序 算法（In-place Sorting Algorithm）。

稳定性分析

原始的数组序列：

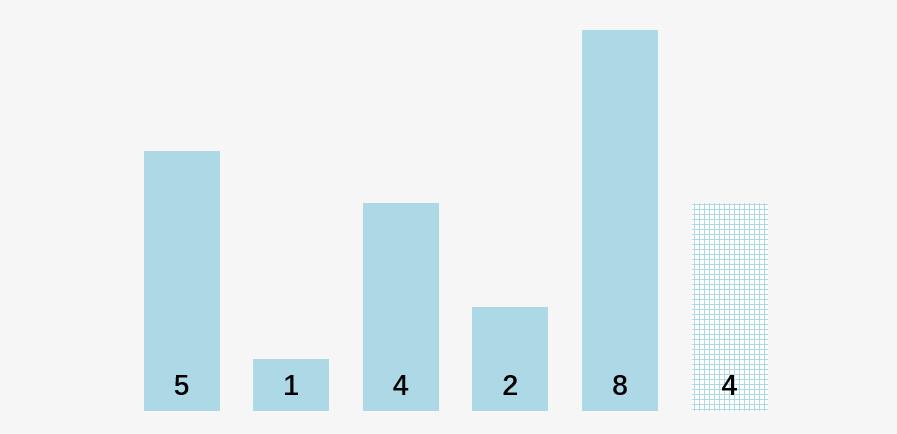
冒泡排序之后的数组序列：

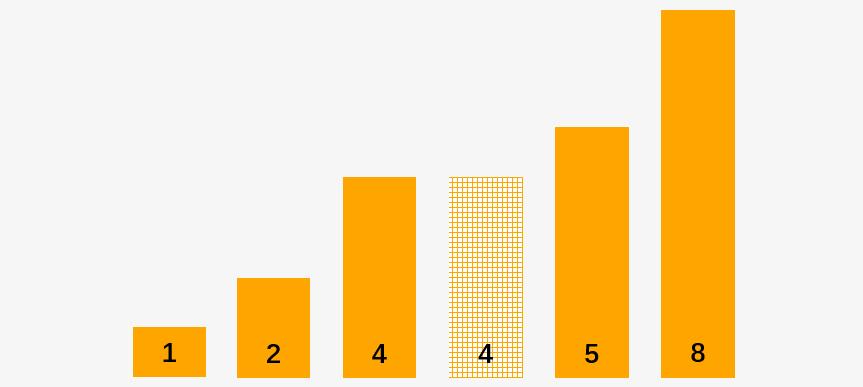
我们可以发现，两个 4 的相对位置没有发生变化，也就是说冒泡排序是稳定的。但这仅相当于实验验证，而在理论上冒泡排序为什么是稳定的呢？

本质原因在于冒泡排序比较和交换的是两个相邻元素，对于键值相同的关键字是不交换位置的，所以排序前后键值相同的关键字的相对位置才保持不变的。

实战演练

如何使用递归实现冒泡排序？

使用递归来实现冒泡排序在性能和实现方式上并无优势，但是用来检查你对于冒泡排序和递归却是一个再好不过的方式。

如果我们仔细研究冒泡排序算法，就会注意到在第一趟冒泡排序中，将最大的元素移到末尾（假设进行升序排列）。在第二趟中，将第二大元素移至倒数第二个位置，依此类推，每一趟冒泡排序的过程是一样的，可以采用递归实现。

这里推荐之前一篇写递归的文章：

递归三要素：

1. 明确你这个函数想要干什么
2. 寻找递归结束条件
3. 找出函数的等价关系式

public class JingYuSorting 
{ 
 // 冒泡排序的递归实现 
    // 1.明确你这个函数想要干什么
    // 函数功能：进行一趟冒泡排序
 static void bubbleSort(int arr[], int n) 
 { 
    // 2.寻找递归结束条件
    // 如果数组只有一个一个元素时，有序，返回
    if (n == 1) 
        return; 
 
  // 3.找出函数的等价关系式
        // 进行一趟冒泡排序
    for (int i=0; i<n-1; i++) 
        if (arr[i] > arr[i+1]) 
       { 
            // 交换 arr[i], arr[i+1] 
            int temp = arr[i]; 
            arr[i] = arr[i+1]; 
            arr[i+1] = temp; 
       } 
 
      // 找到了数组最大的元素
      // 递归对除最大元素之外的数组进行冒泡排序
      bubbleSort(arr, n-1); 
    } 
} 

如何使用两个栈实现冒泡排序？

对于这个问题本身，你可能会觉得没有任何意义，但是当你去努力实现的时候，就会发现，你对于栈和冒泡排序的理解有了新的见解。

问题本身不难理解，就是利用两个栈，然后每一次选择出数组中最大的元素，并存入数组对应的位置。但是当你自己去实现时，还是会发现好多问题，比如如何互换着使用两个栈？如何对栈中相邻的两个元素比较大小，并交换位置？

记得自己尝试着实现一下，一定对你的学习、面试或考试有帮助。

下面是参考的思路：

给定两个栈 s1 和 s2 ，以及一个长度为 n 的数组 arr :

1. 将数组 arr 中的所有元素压入栈 s1 当中；
2. 执行 for 循环 n 次（每一次选择出一个最大的元素）：
• 情况一： s1 不为空， s2 为空，则尝试将栈 s1 当中的所有元素压入栈 s2 ，并保证 s2 的栈顶元素为最大值；当 s1 为空时， s2 中的栈顶元素即为栈中元素的最大值，插入数组相应位置。
• 情况二： s2 不为空， s1 为空，则尝试将栈 s2 当中的所有元素压入栈 s1 ，并保证 s1 的栈顶元素为最大值；当 s2 为空时， s1 中的栈顶元素即为栈中元素的最大值，插入数组相应位置。

详细解析

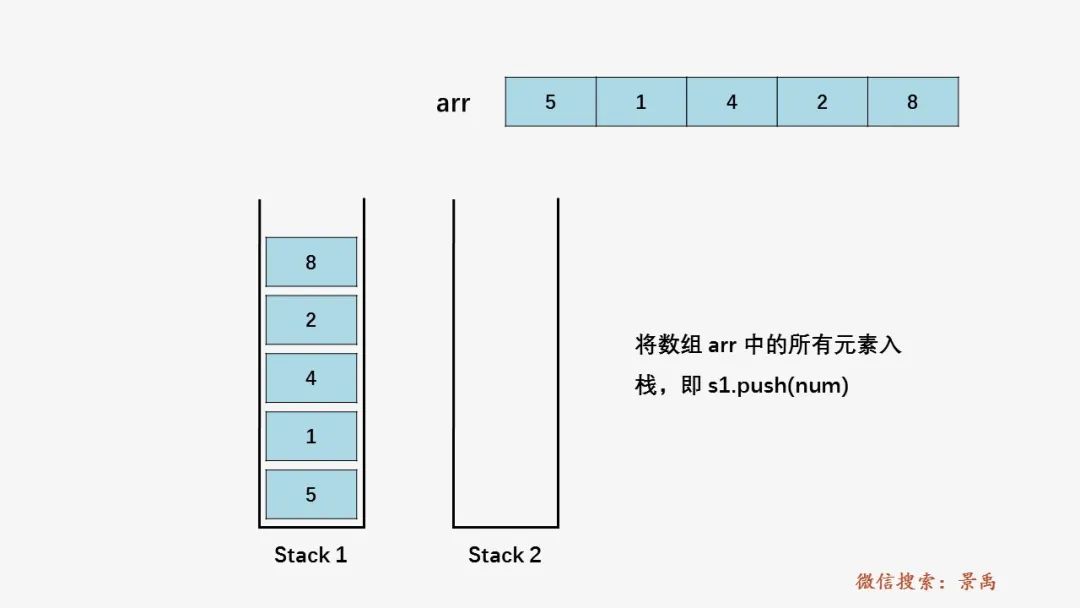
初始时两个栈 s1 和 s2 都为空栈，数组 arr[] = [5,1,4,2,8] 。

第一步：将数组 arr 中的所有元素都压入栈 s1 当中：

第二步：栈 s2 为空，直接将 s1 的栈顶元素 8 压入栈 s2

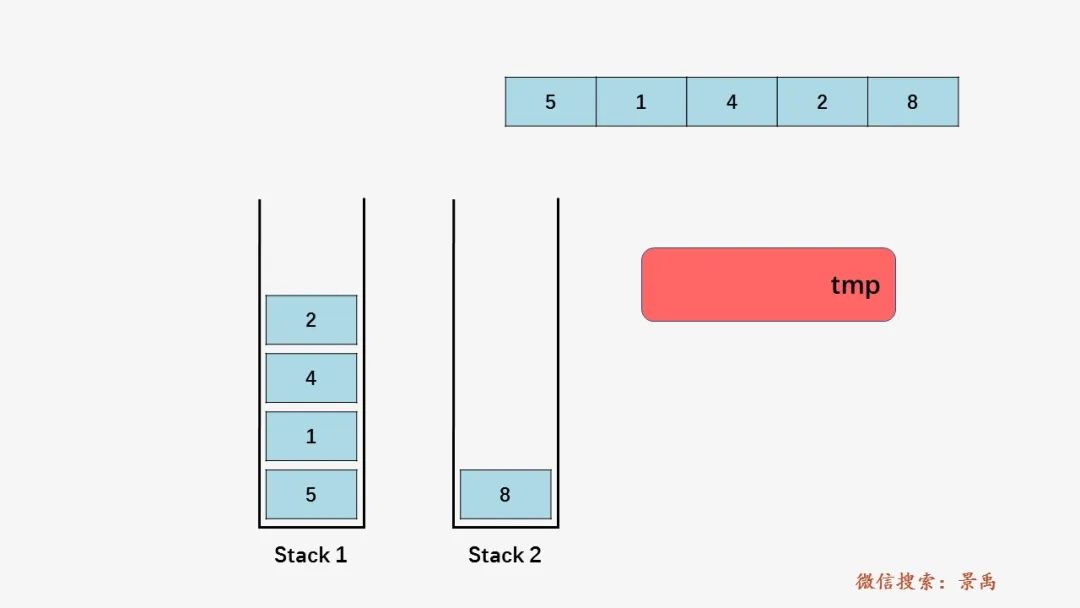
第三步：栈 s1 不为空，尝试将 s1 的栈顶元素 2 压入栈 s2 ，但是此时 s2 的栈顶元素 8  > 2，所以利用一个临时变量 tmp 交换两个元素在栈中的位置，先将 s2 的栈顶 8 保存到 tmp 并弹出，然后压入元素 2 ，最后再将 8 重新入栈。(其实就是交换操作)

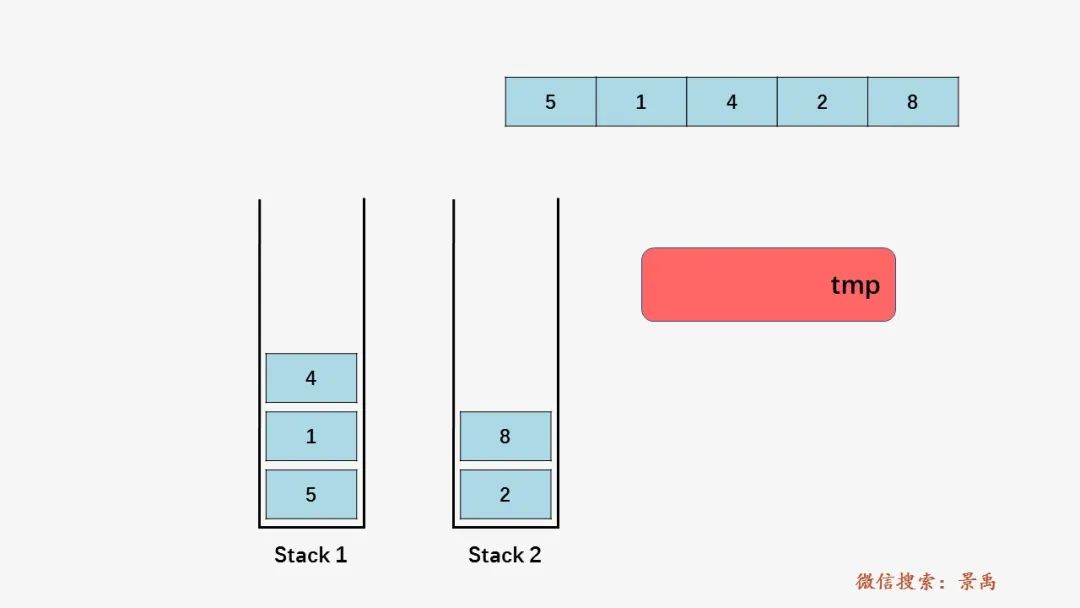
第四步：栈 s1 不为空，同第三步一样将 s1 的栈顶元素压入栈 s2  当中：

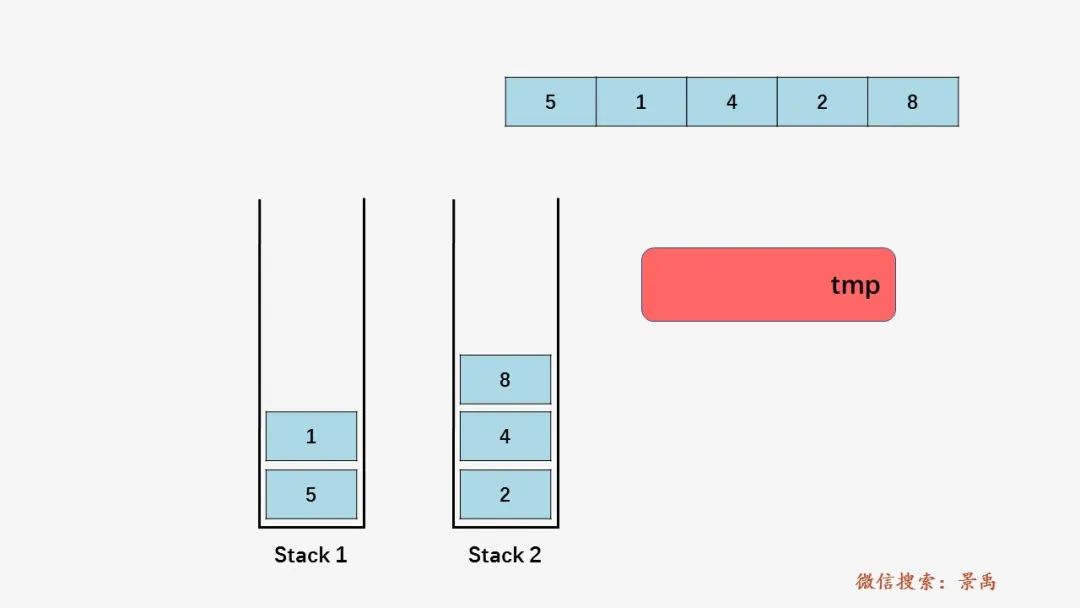
第五步：栈 s1 不为空，同上将s1 的栈顶元素 1 压入栈 s2  当中：

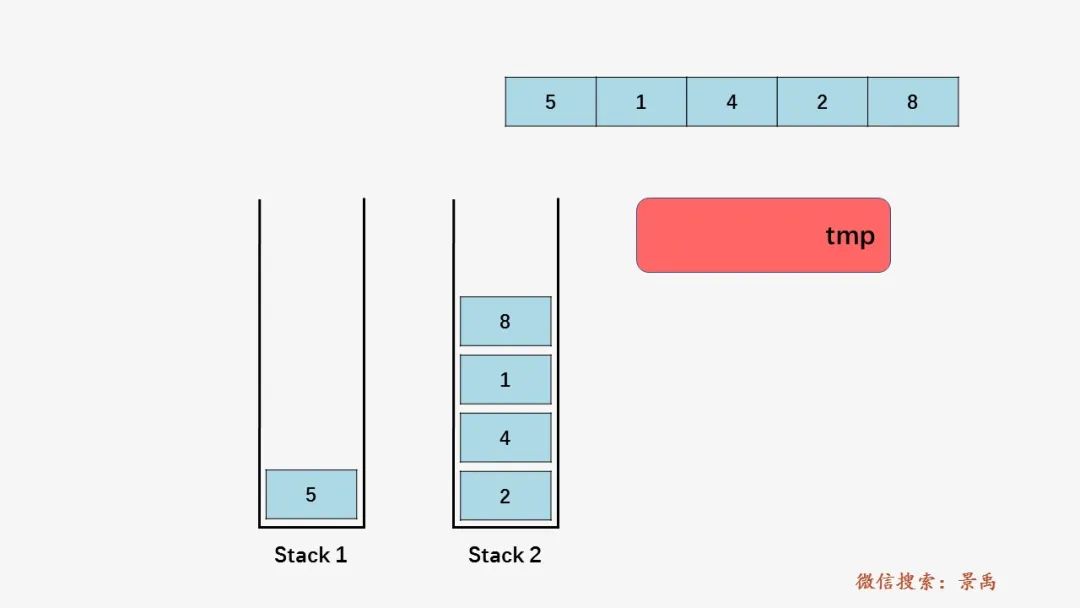
第五步：栈 s1 不为空，同上将s1 的栈顶元素 5 压入栈 s2  当中：

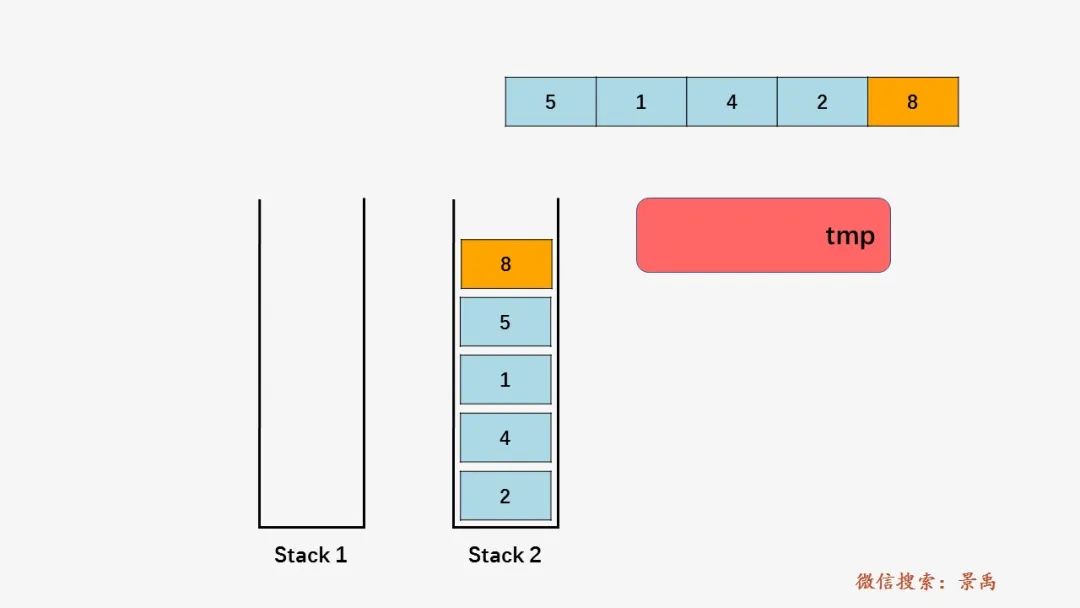
第六步：栈 s1 为空，弹出 s2 的栈顶元素，并将其放到数组 arr[n - i - 1] 的位置：

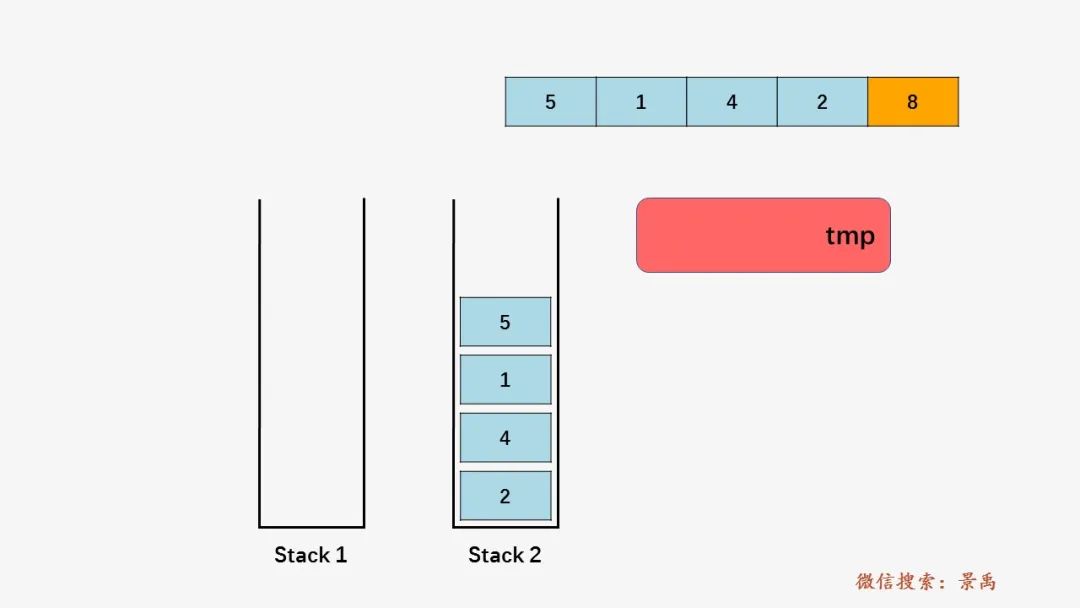
之后的过程和前面讲的类似，将栈 s2 中的元素压入栈 s1 当中，并找到次大元素 5 ，以此类推，实现对数组的冒泡排序。

动画演示

实现代码

public class BubbleSort
{ 
 // 使用栈进行冒泡排序 
static void bubbleSortStack(int arr[], int n) 
{ 
    Stack<Integer> s1 = new Stack<>(); 
  
    // 将 arr 中的所有元素压入栈 s1
    for (int num : arr) 
        s1.push(num);  
  
    Stack<Integer> s2 = new Stack<>(); 
  
    for (int i = 0; i < n; i++) 
    { 
       // 初始时 s1 不为空，使用i 的奇偶来决定将哪一个栈中的元素转移到另外一个栈
       if (i % 2 == 0) 
       { 
            while (!s1.isEmpty()) 
            { 
                 int t = s1.pop(); 
     
                 if (s2.isEmpty()) 
                     s2.push(t);      
                 else
                 { 
                      if (s2.peek() > t) 
                      { 
                           // 交换操作 
                           int temp = s2.pop(); 
                           s2.push(t); 
                           s2.push(temp); 
                      } 
                      else
                      { 
                           s2.push(t); 
                  } 
             } 
        } 
    
        // 将找到的最大元素放到正确的位置 n-i-1 
        arr[n-1-i] = s2.pop(); 
       }    
       else
       { 
            while(!s2.isEmpty()) 
            { 
                 int t = s2.pop(); 
     
                 if (s1.isEmpty()) 
                      s1.push(t); 
                 else
                 { 
                      if (s1.peek() > t) 
                      {  
                           int temp = s1.pop(); 
                           s1.push(t); 
                           s1.push(temp); 
                      } 
                      else
                           s1.push(t); 
                  } 
            } 
            arr[n-1-i] = s1.pop(); 
        } 
    }   
    System.out.println(Arrays.toString(arr)); 
 } 
 
     // 主方法
     public static void main(String[] args) 
     { 
          int arr[] = {5, 1, 4, 2, 8};  
          bubbleSortStack(arr, arr.length); 
     } 
}

如何使用冒泡排序对单链表进行排序？

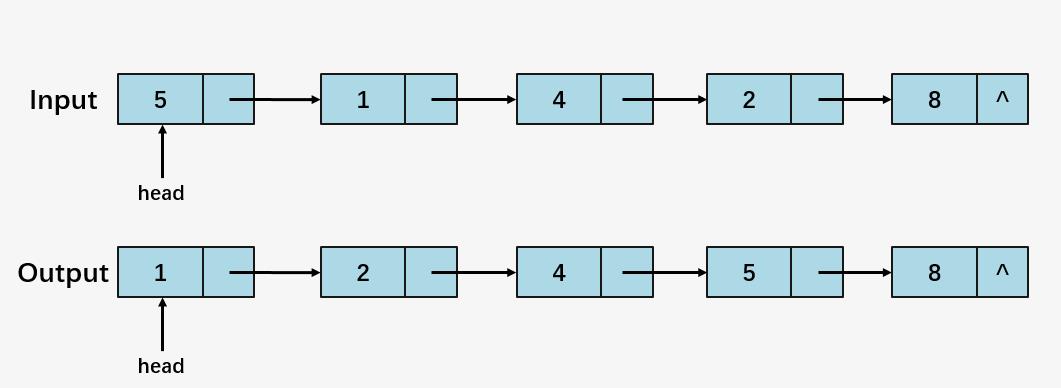
这道题目本身并不难，主要是考察一下各位单链表的知识点，还有对冒泡排序进行巩固。单链表的文章推荐看： 。

最自然的实现方式就是比较相邻的两个结点，如果前面结点的值大于 next 结点的值，则交换两个结点的值，具体如下。

第一趟冒泡排序（仅交换结点的值）

第一步：指针 ptr1 指向头结点 head ，ptr1->next 则指向了值为 1 的结点；

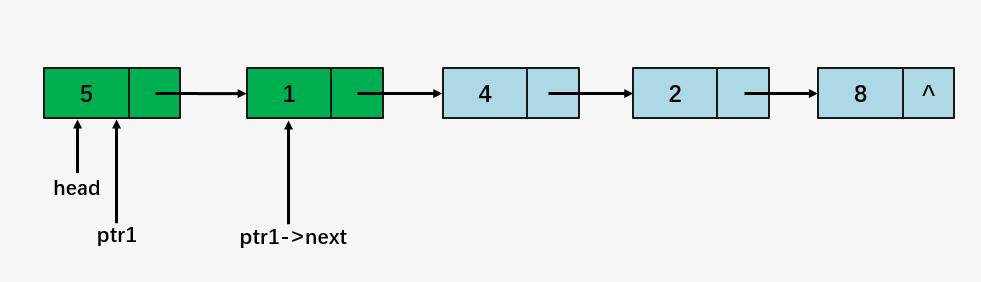
比较 ptr1 指向的结点的值 5 > ptr1->next  的值 1，交换两个结点的值，ptr1 = ptr1 ->next ：

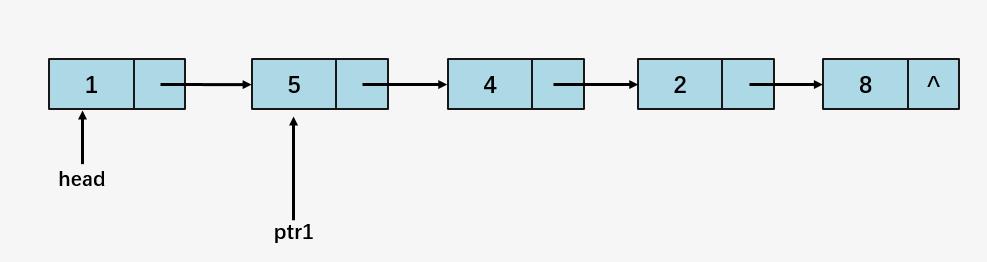
第二步：比较 5 和 4，5 > 4，交换 5 和 4 的值，ptr1 = ptr1 ->next ：

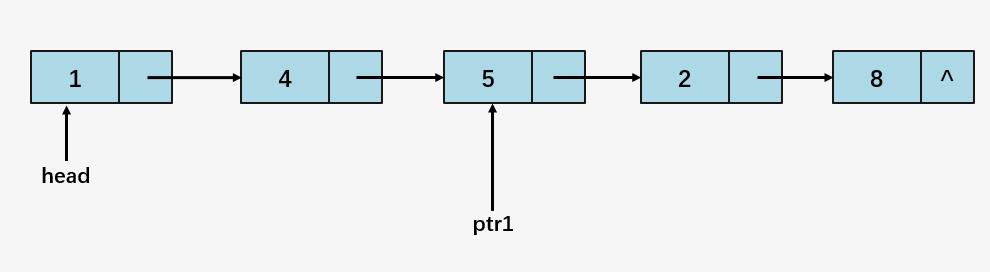
第四步：比较 5 和 2，5 > 2，交换 5 和 2 的值，ptr1 = ptr1 ->next ：

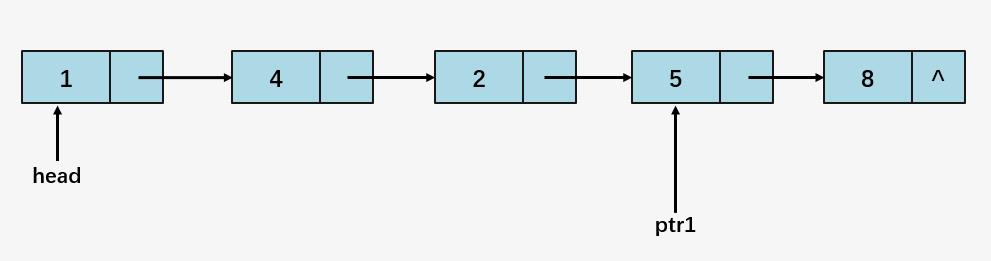
第五步：比较 5 和 8，5 < 8，不交换，ptr1 = ptr1 ->next ，然后用指针 lptr 指向 ptr1 ，再将 ptr1 = head 。

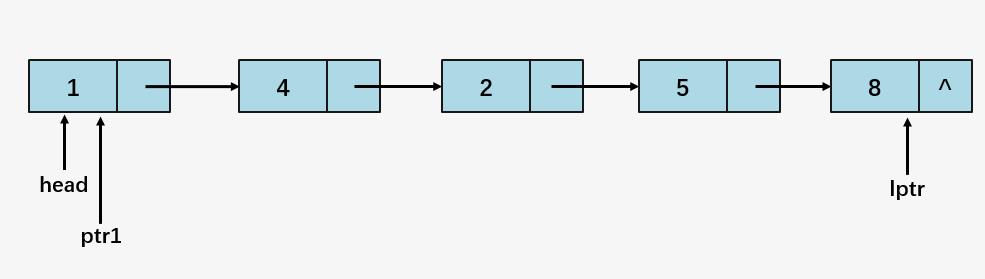
通过一趟冒泡排序找到单链表中最大的值 8 ，并用指针 lptr 标识当前最大的元素。第二趟冒泡以同样的方式找到次大元素 5， lptr 指向 5 ，以此类推，得到最终的有序单链表。

实现代码

/* 单链表上的冒泡排序（交换值的方式） */
void bubbleSort(struct Node *start) 
{ 
  int swapped, i; 
  struct Node *ptr1; 
    struct Node *lptr = NULL; 

    /* 检查单链表是否为空 */
    if (start == NULL) 
        return; 
    //数组有序时退出循环
    do
   { 
        swapped = 0; //标识单链表是否已经有序，0有序，1无序
        ptr1 = start; 

        while (ptr1->next != lptr) 
       { 
            if (ptr1->data > ptr1->next->data) 
           { 
                swap(ptr1, ptr1->next); 
                swapped = 1; 
           } 
           ptr1 = ptr1->next; 
      } 
      lptr = ptr1; 
    } while (swapped); 
} 

/* 交换单链表两个结点的值*/
void swap(struct Node *a, struct Node *b) 
{ 
    int temp = a->data; 
    a->data = b->data; 
    b->data = temp; 
} 

上面这种方式的确实现了单链表的冒泡排序（通过值的方式），但是如果面试官或考官问你，我们通过 交换结点本身 的方式对单链表进行排序，又该如何实现呢？

交换结点本身比交换结点的值稍微复杂一些，但是只要细心一点，也没有问题，我们还是以上面的例子说明。

第一趟冒泡排序（交换结点本身）

第一步：定义指向头结点的指针 h ，并将 p1 指向与 h 相同的位置，p2 指向 p1->next ；

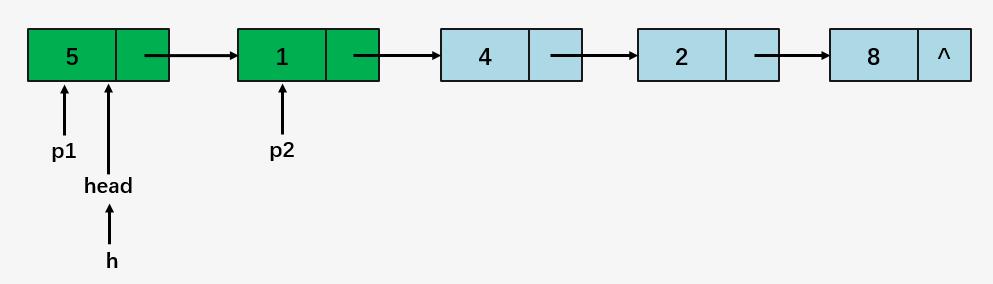
比较 p1 指向的结点和 p2 指向的两个结点的大小，然后将 p1 和 p2 进行交换：

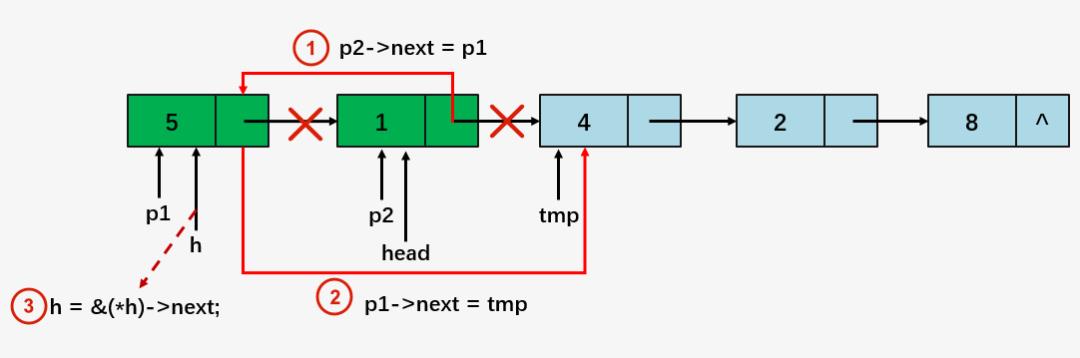
1. 将指针 p2->next 指向 p1
2. p1->next = p2
3. h = &(*h)->next
4. head = p2

即得到如下形式：

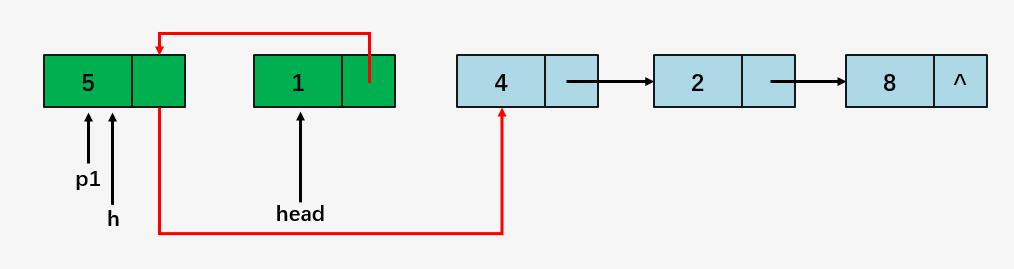
第二步：p1 = h ，p2 = p1->next ，比较 p1 和 p2 :

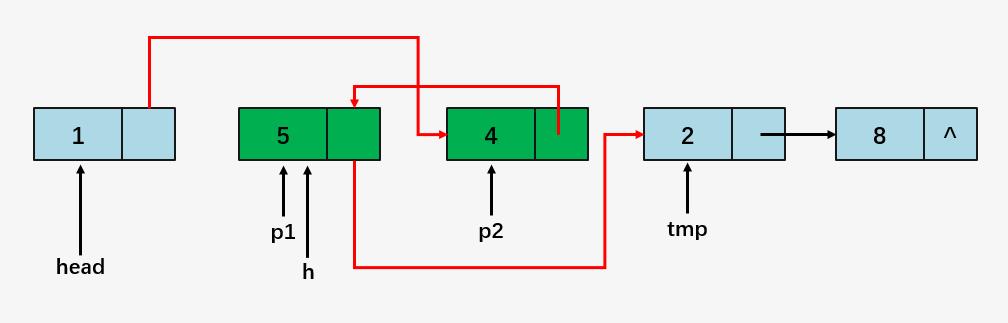
整个步骤最关键的就是结点交换后指针的修改，可以参考代码再理解理解！里面涉及的指针操作比较多，但是冒泡排序的整个代码框架没有变化。

/*交换结点 */
struct Node* swap(struct Node* ptr1, struct Node* ptr2) 
{ 
    struct Node* tmp = ptr2->next; 
    ptr2->next = ptr1; 
    ptr1->next = tmp; 
    return ptr2; 
} 

/* 对单链表进行冒泡排序 */
int bubbleSort(struct Node** head, int count) 
{ 
    struct Node** h; 
    int i, j, swapped; 

    for (i = 0; i <= count; i++) 
    { 
        h = head; 
        swapped = 0; 
        for (j = 0; j < count - i - 1; j++) 
        { 
            struct Node* p1 = *h; 
            struct Node* p2 = p1->next; 

            if (p1->data > p2->data) 
            { 
                /* 交换结点之后修改链接 */
                *h = swap(p1, p2); 
                swapped = 1; 
             } 
             h = &(*h)->next; 
     } 

      /* 如果没有任何交换操作，链表有序 */
      if (swapped == 0) 
          break; 
    } 
} 

请使用冒泡排序对字符串数组进行排序

最后来个简单的，让大家获得一定的成就感，这样才能继续前行~~

冒泡排序为什么叫冒泡呢？

大家一定都喝过可口可乐之类的碳酸饮料，碳酸类饮料中常常有许多小小的气泡，哗啦哗啦向上冒。这是因为组成小气泡的二氧化碳比水要 轻 ，所以小气泡都向上冒。冒泡排序也是一样，每一趟冒泡排序都会让最小的元素浮出水面（降序排列），所以很形象地命名为冒泡，也欢迎大家评论区冒泡呀！让景禹见见你~

字符串排序相当简单就不给大家解释了，我想你心里都写出了代码，仅供参考：

public static void sortStrings(String[] arr, int n) 
{ 
     String temp; 

     for (int j = 0; j < n - 1; j++) 
     { 
          for (int i = j + 1; i < n; i++) 
          { 
                if (arr[j].compareTo(arr[i]) > 0) 
                { 
                     temp = arr[j]; 
                     arr[j] = arr[i]; 
                     arr[i] = temp; 
                } 
           } 
      } 
} 

好好学习，天天向上呢~~

推荐阅读：

点个在看，对你们爱爱爱爱不完