运筹学 class03 网络模型-最小生成树

Posted 2021-04-07 计算机算法与模型

大量的运筹学问题都可以通过网络（节点之间通过边联通）来建模求解：

（1）在墨西哥湾需要设计一个海上天然气管道网络，将各个井口连接到岸边的运输点。模型的目标是使建设管道的费用最小化。

（2）在已有的道路网络中，求两个城市之间的最短路径。

（3）求从怀俄明的煤矿到休斯顿的发电厂的煤浆管道网络的最大运输量。

（4）为一个工程项目中的各项活动确定时间表

（5）确定后从油田到炼油厂的管道网络的最小费用流。

对于上述情形的求解均可以使用网络优化算法，本系列课程将通过matlab介绍其中的四种算法

• 最小生成树算法

• 最短路径算法

• 最大流算法

• 关键路径算法

案例一、中西部有线电视公司接话为五个新的居民区提供有线电视服务，图给出小区之间铺设电缆的情况以及相应的距离。问题是：确定最经济的电缆铺设方案，使五个小区可以连接起来。

源代码：

s = [1 1 1 1 2 2 2 3 3 4 4 ];t = [2 5 3 4 3 5 4 4 6 5 6 ];weights = [1 9 5 7 6 3 4 5 10 8 3];names = {'1' '2' '3' '4' '5' '6'};G = graph(s,t,weights,names)p = plot(G,'EdgeLabel',G.Edges.Weight);
[T,pred] = minspantree(G);highlight(p,T)

运行结果：

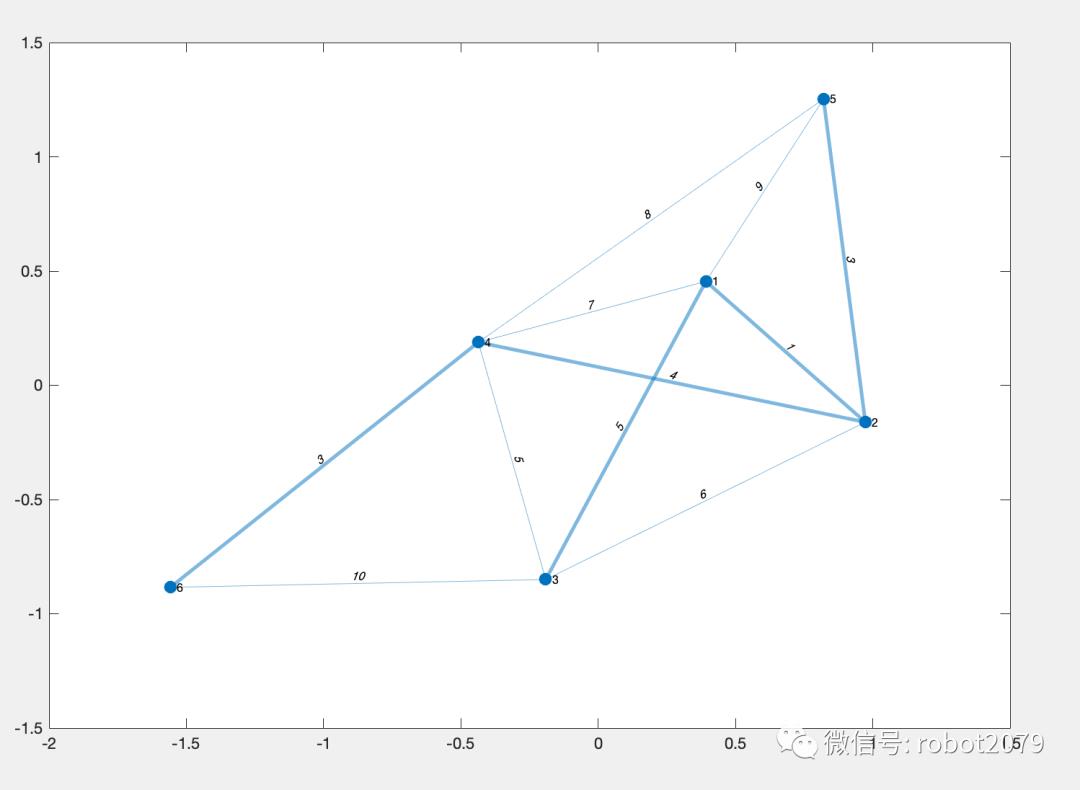
不求赏赞，只求在看