如何确定股票的联动效应?基于网络模型的择时研究
Posted XYQUANT
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何确定股票的联动效应?基于网络模型的择时研究相关的知识,希望对你有一定的参考价值。
导读
1、作为西学东渐--海外文献推荐系列报告第四十四篇,本文推荐了KOUSHIK BALASUBRAMANIAN等人于2019年发表的论文《Do Stocks Stalk Other Stocks in Their Complex Network? A Complex Networks Approach to Stock Market Dynamics》。
2 、金融析师在建模、分析和监测全球金融体系的实质联动性方面明显存在滞后,人们一般无法提前预测金融危机的来临。然而,许多研究表明,在金融危机期间,股票之间的相关性往往会表现出不一样的特质。这正是本文所研究的焦点。
3、 我们知道,在系统性风险出现后,股票收益率之间的相关性增加,这也表明基于相关性的指标不适合作为危机的预警指标。本文基于相关网络模型与动态网络模型建立多个指标捕捉金融危机期间的股票联动性变化,研究发现这些指标可以作为恢复阶段的早期预警指标。同时文中提供了构建这些网络的详细说明。
4、 文章提出将新闻和公告等因素加入模型的想法,可以分析危机期间新闻和公告的影响。同时文中也给出了结合新闻和公告对动态网络模型进行简单修改的意见。
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成, 在政策、市场环境发生变化时模型存在失效的风险。
一、引言
金融危机期间,股票之间的平均相关性往往会增加,市场波动性也会极大的提升,这时股票收益率不再遵循正态分布。这也意味着,用非金融危机期间股票的历史概率分布来分析金融危机期间的市场往往会产生错误的结论。例如2007年的次贷危机,人们一般认为瀑布式支付结构会限制结构性债务抵押债券的损失,然而正是这种认知在2007年导致了整体性损失。
同时,金融危机期间,股票无论是地理上还是行业上的分散化投资,都失效了,除黄金(或一些避险资产)以外的大多数商品普遍出现下跌。投资组合是否能够真正的实现多元化是一个原因,另一个原因是在金融危机期间资产收益率是非正态的。金融危机期美国股市的波动幅度约为3-4个标准差,可以发现联动性是真实存在的。
2011年,葡萄牙、意大利、西班牙和希腊资产的大幅缩水导致了欧元经济危机,债券和股票都未能逃脱这次危机。2007年与2011年的两次危机表明,金融分析师在建模、分析和监测全球金融体系的实质联动性方面明显存在滞后。由于人们未能提前预测到这场危机,雷曼兄弟(Lehman Brothers)和贝尔斯登(Bear Stearns)等实体破产以及希腊等主权国家的问题形成了多米诺骨牌效应,带来系统性损失。
世界银行独立评估小组(2011年)和国际货币基金组织的分析师对金融危机进行了深入的研究,研究表明:收益率的分布具有明显的厚尾、尖峰和极端的峰度等特征。然而在建模中,资产收益率的这些性质经常被忽略,因此不能准确地反映这些相对罕见的事件。实际上,这些事件发生的可能性比由正态分布计算的可能性更高。人们常用的风险指标(Adrian和Brunnermeier(2016)的风险条件值,Acharya等人的短缺指标以及Brownlees和Engle(2017)定义的系统性风险)可能会带来潜在的误导性。
Billio(2010)和Kritzman等人(2011)提出可以使用主成分分析(PCA)得到某些市场稳定性指标。其中Kritzman等人(2011)的吸收率指标和Billio等人(2010)的累积风险分数度量都与相关矩阵的特征值有关。这些研究都指出,金融资产收益率的相互联动性在危机期间增加。
Mantegna(1999)提出了一个基于相关矩阵的距离度量,将受共同经济因素影响的股票组进行分类。使用相关性度量获得的分组可以通过经济变量来解释(或标记)。这种分组的数量可以被视为影响市场的这些金融变量的量度。实证研究表明,在金融危机期间,金融资产往往以相关的方式移动,导致资产过于集中。如果资产可以分组为少数集群,那么可以预期少数因素会影响市场。这些因素的不稳定性会立即影响众多资产,从而导致众多资产一起出现下跌。
近年来的许多研究探讨了资产之间相关性,更确切地说,主要研究利用网络方法来量化传染效应并解释稳定和不稳定股票之间的结构差异(例如,Ang和Chen 2002; Cappiello,Engle和Sheppard 2006; Jiang和Zhou 2010; Das 2016; Li et al。2016; Cao,Shi和Li 2017; Kim和Sayama 2017; Xu et al。2017; Das,Kim和Ostrov 2019)。所有这些论文都提供了使用网络方法来分析金融危机的有效性的实证结果; 然而,金融市场在复苏阶段附近的行为并没有受到太多关注。Das(2016)指出,在系统性风险出现后,股票收益率之间的相关性增加,表明基于相关性的指标不适合作为危机的预警指标。然而,本文指出这些指标(基于相关性)可以作为恢复阶段的早期预警指标。
本文第一部分分析了相关网络并计算了在恢复期附近有特殊表现的指标。借鉴Xu等人(2017)的做法,本文使用t检验来对相关矩阵(或称为关联矩阵)进行过滤。同时使用该相关矩阵的元素来构建图(Graph)。接着,我们计算指标来度量一个节点相邻节点的数量,这也被称为节点的度(degree of a node)。该指标在给定时间点附近呈现出潮汐进退(tide-in tide-out pattern)模式,可用于产生危机和恢复信号。我们观察到,当市场处于从危机中复苏的时候,这种分布的时间依赖均值达到局部最大值。
我们还采用多维缩放(MDS)技术来提取低维潜在空间中的股票。潜在空间中股票的点云呈现球的形状。在危机期间,这个球的半径增加,并且在恢复附近开始减小。基于Billio等人(2010)和Kritzman等人(2011)的研究,我们推测球体的半径很有可能与相关矩阵的特征值有关,但本文并不打算识别这种关系。主要原因如下:
1) 事实上,使用MDS得到的潜在因素与Billio等(2010)和Kritzman等(2011)使用PCA得到的因素之间似乎没有明显的联系。
2) 虽然流动性、杠杆、位置(positioning)等金融因素很可能与潜在因素(或潜在因素的某些组合)高度相关。大多数传统回归模型假设资产收益与财务因素之间存在函数关系,以分析资产的动态。这也可以用潜在因素而不是财务因素来完成。然而这会产生如何将潜在变量与财务变量联系起来的问题。财务变量通常被认为是可以解释的,其与资产价格之间的因果关系是直观的,通常出自经济学家和金融分析师。然而,确定资产收益与潜在因素之间的因果关系是一项具有挑战性的工作,资产收益的突然变化进一步加大了研究难度。
Billio等人(2010)使用格兰杰因果关系检验来确定基金的收益率(例如,基金i是否对不同的基金j具有因果影响)。他们提出了一个网络,其中网络的节点是所考虑的基金,如果其中一个节点对另一个节点具有因果影响,则这些网络通过边缘连接。他们定义了这些网络关联性的衡量标准,同时发现这些衡量指标在危机期间会增加。但是,如果两个基金i和j由具有不同响应时间的公共因子驱动,则可能会被误认为具有因果关系。早期关于系统性风险的研究表明,在危机期间只有少数因素影响股票价格。这些因素极不可能以完全相同的方式影响所有股票,导致股票收益率对经济因素的不同反应。
本文的第二部分将动态股票网络嵌入潜在空间,并将潜在变量视为经济因素的代理,以对问题进一步理解。
在这个动态网络模型中,每个股票根据其短期趋势,长期趋势和横截面排名分配一个离散标签。然后使用这些标签构建动态网络。观察该特定网络的概率用潜在维度的距离表示。如果股票的潜在维度接近,则两条股票通过边缘(具有相同标签)连接的概率更高。假设潜在变量遵循马尔可夫过程,我们得出在较早时间给定潜在位置观察图的概率。然后通过最大化观察使用标签生成的网络的可能性来确定潜在空间中的股票的位置。然后,我们计算所有股票对之间的滞后距离(其中滞后距离是时间t处的股票i与时间t-1处的股票j之间的距离)。我们观察到,在危机期间,股票之间的滞后距离平均下降,导致股票走向潜在空间中的其他股票。股票的这种移动类似于在社交网络中观察到的跟踪行为的模式。
接下来我们将介绍上述两种网络模型:相关网络模型和动态网络模型。同时提供了构建这些网络的详细说明。我们还提出了结合新闻和公告对动态网络模型进行简单修改的效果,并展示了相关结果。
二、市场的网络模型
2.1
相关网络模型




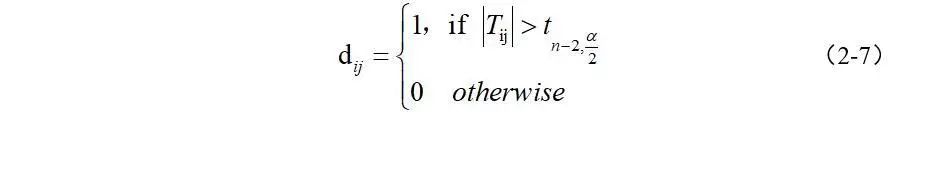
2.2
动态网络模型
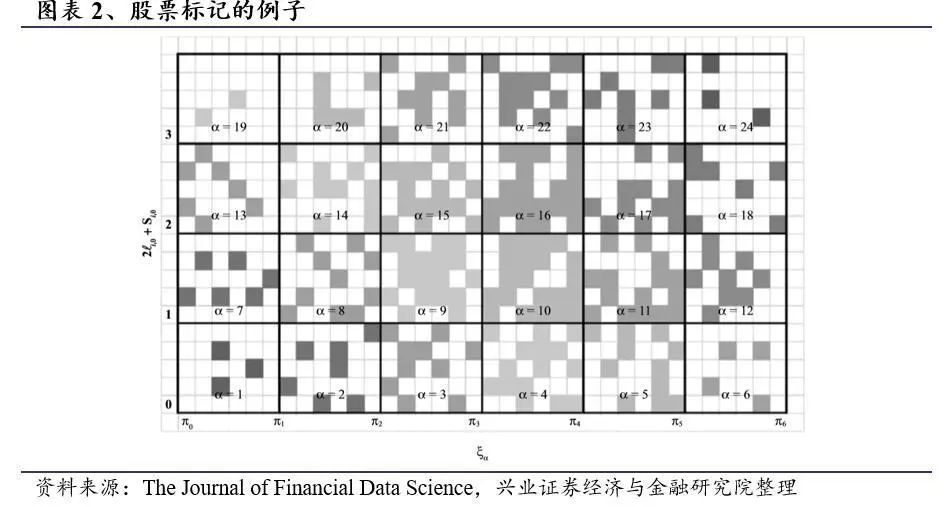
在本小节中,我们提出了股票市场的动态网络模型。在该模型中,我们将候选股票划分为不同的离散集群,并为每个集群给定标签 。
这些标签可以依据额外的财务变量来决定,例如公司收益,商品价格变动,公司信用评级等,并由节点的颜色来表示。但是考虑到计算难度,本文避免了根据财务变量来给定标签,选择了简单了分层技术来确定股票的标签,这使后续计算更容易并且减少了工作量。
2.2.1 网络构建




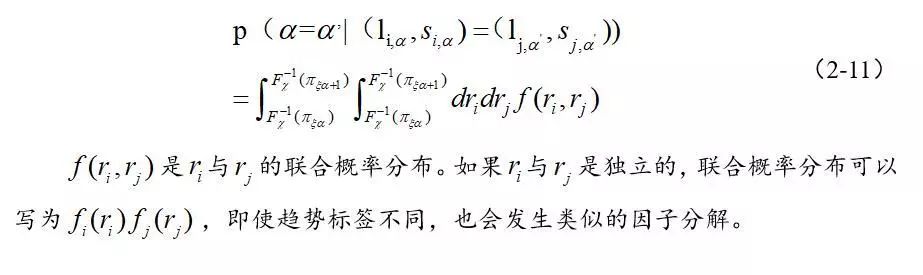


2.2.2 潜在空间构建






2.2.3 纳入新闻和公告影响


三、实证细节
3.1
相关网络的实证细节
对于相关网络,我们使用罗素3000指数成分股(2018年7月31日成分股名单)2000年1月1日至2018年7月31日的每日收盘价构建。同时以下三类股票的数据将被剔除:
1) 在2000年1月1日之后上市
2) 在2018年7月31之前退市的股票
3) 出现缺失值的股票
对于动态网络模型,我们使用罗素3000指数成分股从1995年1月1日到2018年7月31日的每周收盘价构建。
3.1.1 度分布
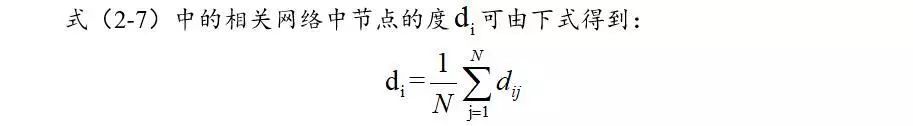

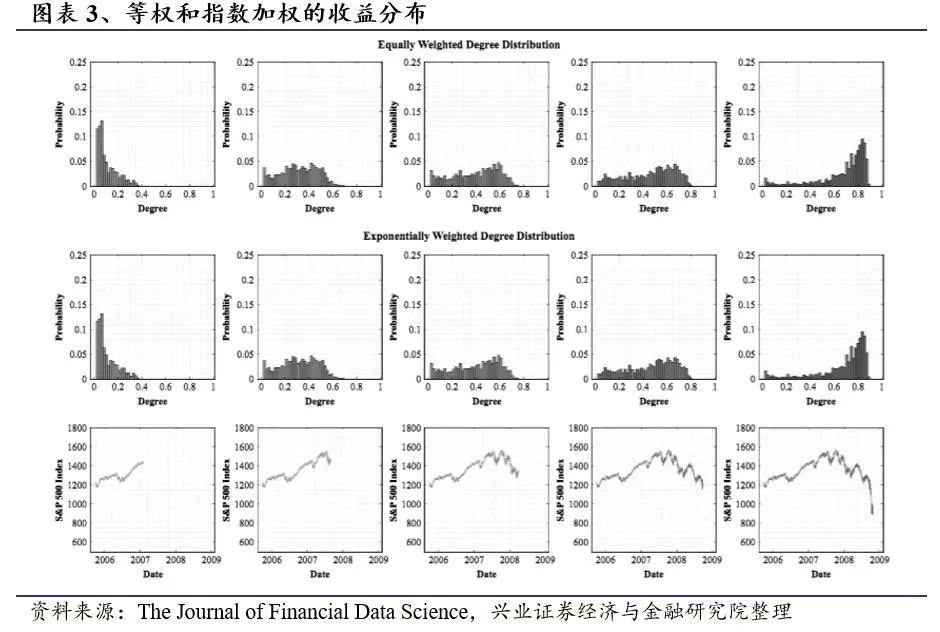
3.1.2 MDS 方法


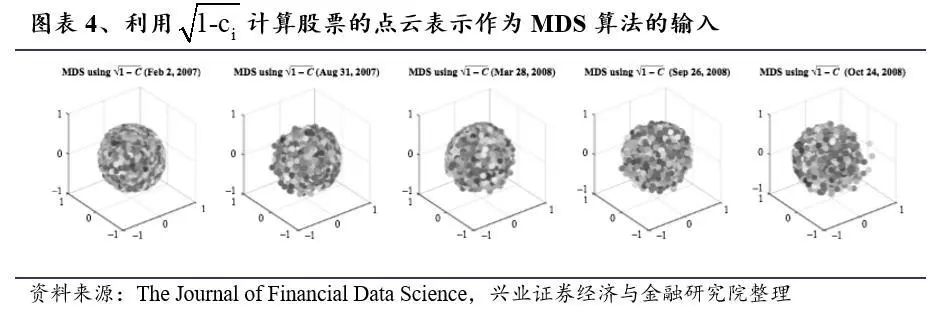
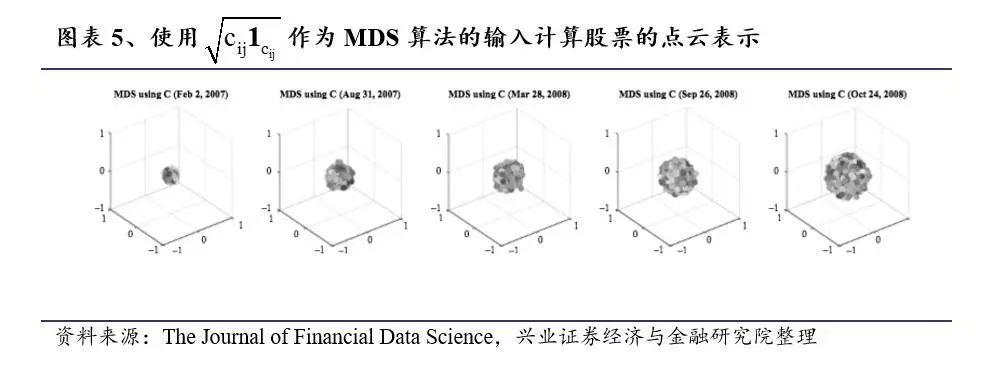
3.2
动态网络模型实证细节
3.2.1 趋势标签
本文使用简单的低通滤波(low-pass filter)方法生成动态网络模型中的趋势标签。低通滤波方法可以保留信号中的低频分量,而将较高频的分量设为0。首先利用快速傅里叶变换将价格序列变换到频域,并将频域信号通过低通滤波器。信号中的高频成分可以与每天和每周的变化相关联。
3.2.2 横截面分位数序数

3.2.3 潜在变量的更新

四、实证结果
本节中,我们将计算:
1)度分布;
2)使用MDS生成的股票的潜在空间表示(3-D)。
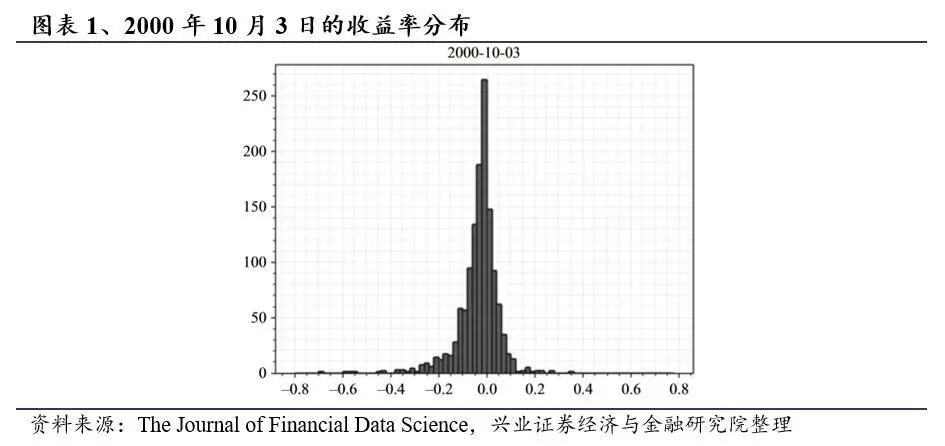
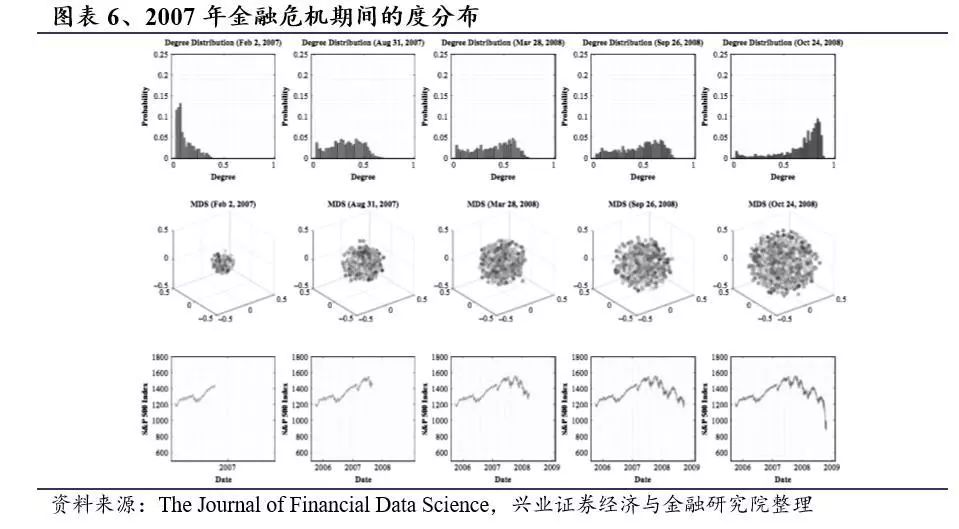
如前所述,我们将使用Cij作为MDS算法中的输入距离矩阵。图表6与图表7最顶部的面板展示了度分布。同时中间的面板为潜在空间的点云表示。第三个面板为同时期标普500的时间序列。
如前所述,如果节点的度很高,则与该节点代表的股票与市场中的许多其他股票相关联。当大量股票以相关方式移动时,度分布会达到较高的峰值并且呈负向偏差; 同时正偏差表明股票没有很好的相关性。股票的点云表示形式为球形, 当股票以相关方式移动时,该球的半径很大,而当股票没有很好地相关时,这个球的半径更小。
图表6和图7表明,在金融危机期间(2007年次贷危机和2011年欧洲主权债务危机),度分布呈潮汐涌入模式。在2007年初的危机前期间,度分布的平均值较低,这表明在此期间股票相互之间的相关性较小。随着我们接近2008年的危机,股票表现出更多的共同运动,度分布的高峰开始逐渐朝正向发展; 分布的偏度变为负值,并且度的最大值增加。随着股票以相关方式移动以及市场变得更加脆弱,点云的半径增加。当市场在2008年10月崩盘时,度分布大幅向右移动并出现大幅负偏差,表明在此期间股票高度相关。
从非危机到危机前到危机的程度分布的演变类似于潮汐现象:在危机前期间波浪持平然后变得陡峭,在到达海岸线时形成高潮,当海浪袭击海岸线时市场崩溃发生。
在图表7中,随着市场在2008年末进一步走跌,度分布的偏度变得更加负,并且峰度值增加。点云在此期间具有大的半径。随后,市场下行趋势缓和,并在2009年初开始减弱。随着危机的缓解,度分布虽然仍然是负面偏离,但却向左侧移动。随着恢复的继续,分布的形状变平,分布的峰度减小。随着市场反弹并开始从危机中恢复,度的最大值也逐渐减小。与此同时,点云的半径达到最大值并开始恢复。在市场完全恢复之后,(危机后)程度分布和点云表示最终会回到危机前的状态。
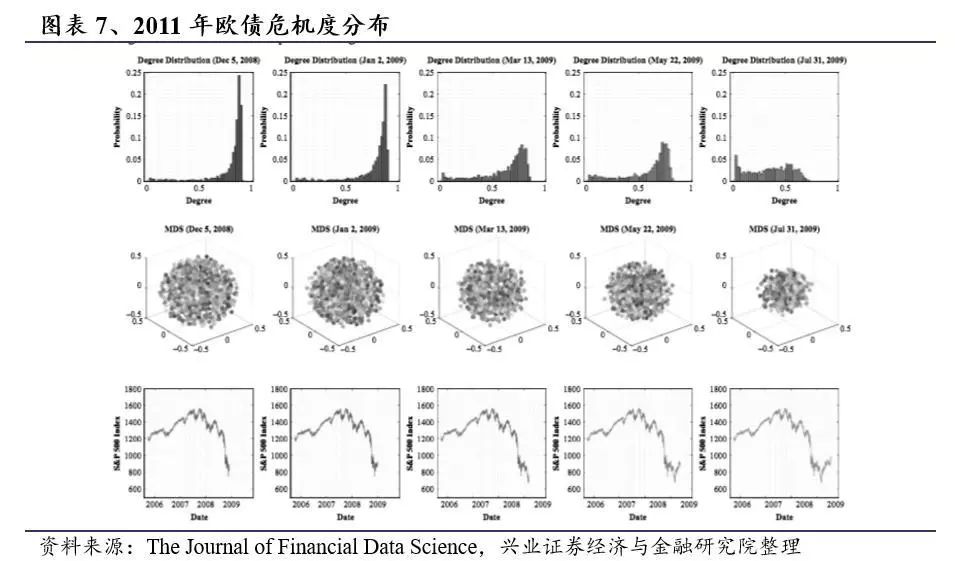
度分布的演变在恢复期呈现出潮汐模式。随着市场从危机中复苏并且市场中股票的价格变化变得更加不相关,分布的负面偏离特征逐渐消失。图表7表明,在危机后或复苏阶段,股票之间的相关性较小。
通过计算波动率调整后的平均度与标准普尔500指数,可以进一步详细说明结果,计算方法如下:
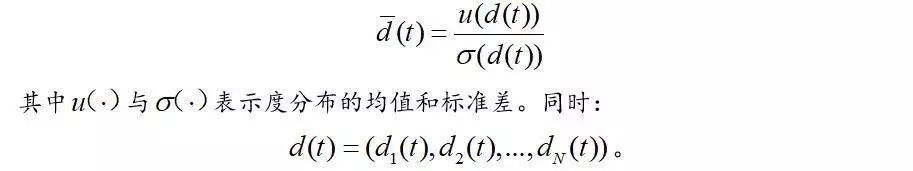
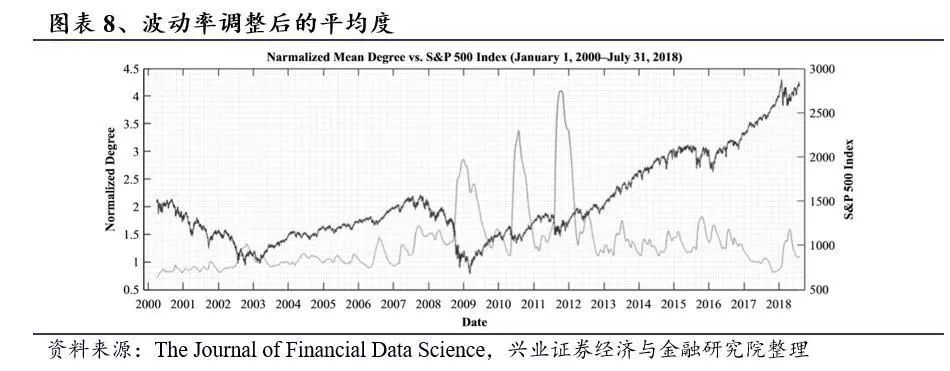
如图表8所示,在2007年初至2008年中期的危机前期间,波动率调整后度逐渐增加,市场中股票之间的相关性增加。随着市场崩盘而市场触底反弹,调整后的度急剧上升。波动率调整后的度从2009年(2007年次贷危机结束)市场复苏之前的高峰时期开始冷却,并且在欧洲债务危机引发的两次主要市场崩溃结束时表现出类似的后危机行为。结果表明,波动率调整的度,以及从度分布可能得出的其他复杂指标,可以作为市场复苏的潜在领先指标(在重大危机之后)。
4.2
动态网络模型实证结果
本文选择m = 10, 即标签总数为40。使用前面描述的方法,给定股票从1995年1月1日到2018年7月31日每一天的标签。
图表9为股票标签的热图。在该热图中,图中每个点的颜色表示给定时间(垂直轴)的每只股票(横轴)的标签。较暗的阴影表示较小的标签,较亮的阴影表示较大的标签。如果当天没有股票的价格数据,则该点的颜色设置为白色。
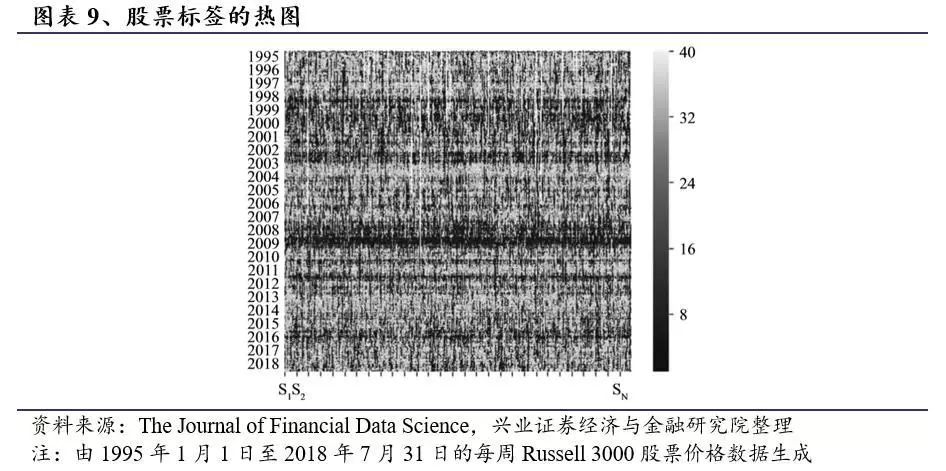
在图表9中,我们看到在1999年左右开始出现黑暗的水平线条,即此时大量的股票都在标签较小的层中。这也意味着大量股票在1999年开始的时期内具有向下的短期和长期趋势。这一时期恰好是互联网公司泡沫导致市场过热。当我们接近次贷危机和欧洲债务危机时,热图在2007年和2011年左右呈现出相同的模式。在这些重大市场危机之后,2002年,2009年和2011年市场复苏开始时,水平线的颜色开始变淡。较浅的水平线对应于大多数股票被分配较高标签的市场,表明向上的长期和/或短期趋势。
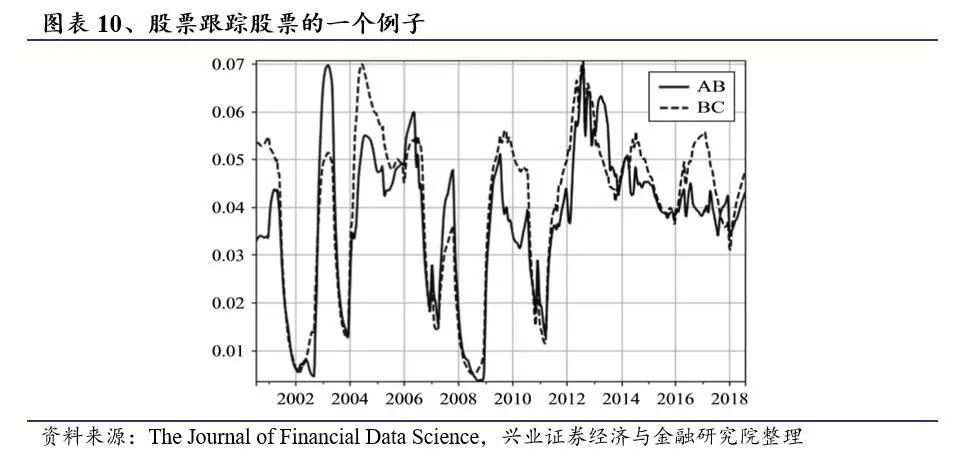
在危机期间,股票市场受到少数金融因素的影响,导致股票之间的集体行为(Billio等人,2010; Kritzman等人,2011)。图表9的热图证实了这一想法。虽然股票走势的方向可以由一小部分金融因素决定,但人们预计股票对这些因素的反应时间会有所不同(实际上,幅度也可能不同)。响应时间的滞后将导致股票在因素(物理经济因素)空间中跟踪股票。我们观察到可以在潜在空间中观察到这种跟踪行为。图表10显示,在危机期间,某些股票在时间t和t-1的潜在仓位之间的滞后距离减少,这表明每对中的一只股票正在跟踪另一只股票。
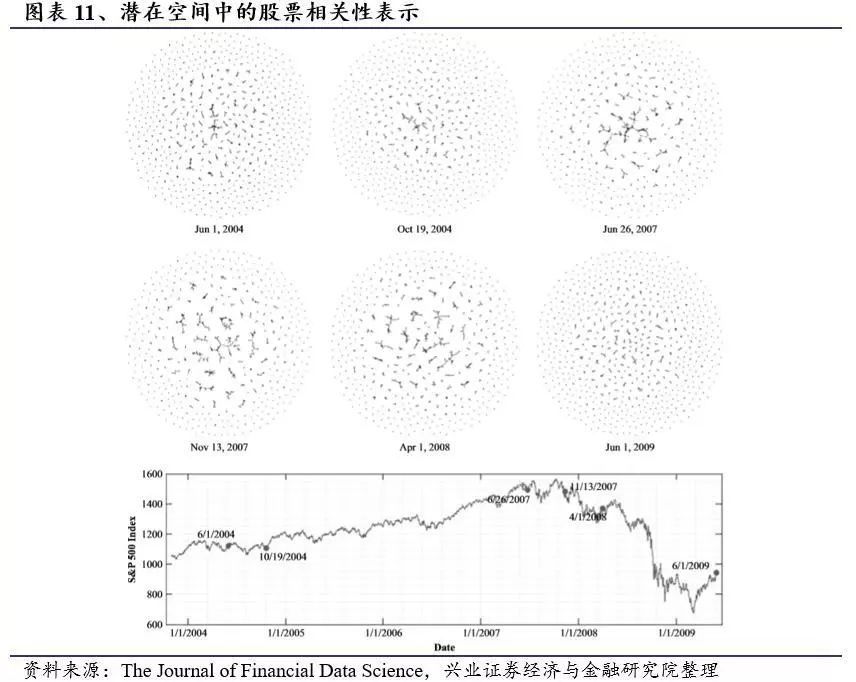
我们可以使用图表11中的股票的网络表示来推断这一点。该图中节点的位置不应与潜在空间坐标混淆。仅当潜在空间中它们(或股票)之间的滞后距离(或跟踪距离)小于阈值ε时,才连接该图中的两个节点。我们选择ε= 0.004来生成图表11中的网络(选择较大的阈值会导致杂乱的图形具有更多的边缘和集群, 使用一个小阈值更便于清楚地了解簇的形成和分解)。请注意,图表11中显示的网络是有向图,但我们没有显示箭头,因为跟踪的方向与我们的讨论无关。节点i和j之间的双线表示股票Si跟随Sj并且Sj跟随Si的情况。在这种情况下,很难将引领者与追随者区分开来。节点i和j之间的单个线表示只有一个股票跟随另一个股票的情况。
图表11显示,在2007年底(次贷危机开始),股票形成了更大的集群。
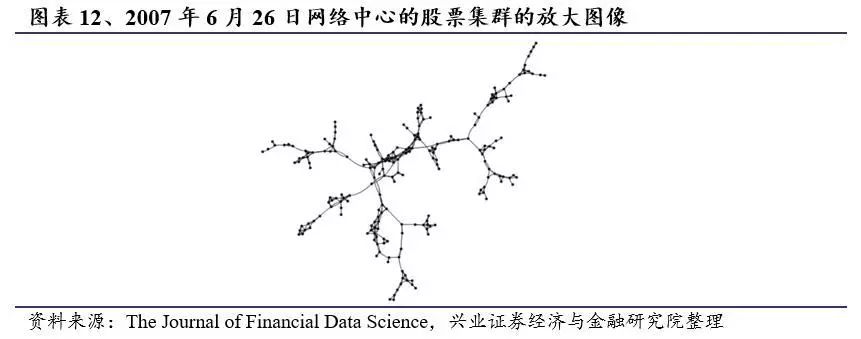
图表12显示了2007年6月网络中心观察到的大型集群的放大图像。随着危机的结束,集群开始崩溃,市场在2009年初开始反弹。
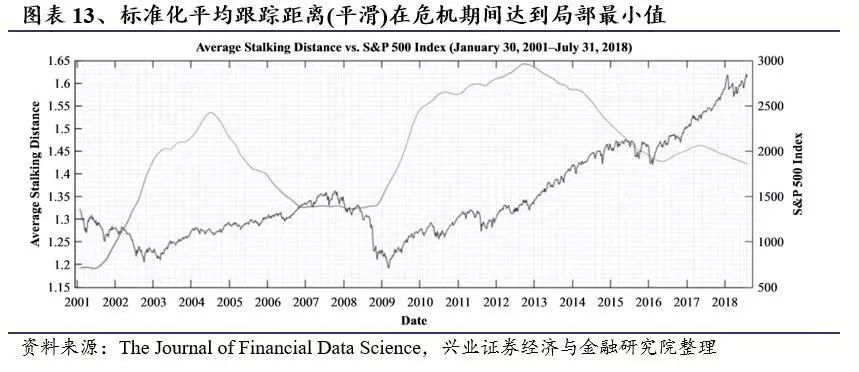
图表13显示了滞后距离的横截面平均值的时间序列。我们可以看到该指标在主要危机时期附近达到局部最小值。
五、结论
我们的研究表明,股票收益序列对经济因素的差异反应导致了股票市场网络的跟踪模式。平均滞后距离的倒数是一个简单的度量,可以用来量化网络跟踪的程度。同时,我们发现,跟踪程度在危机时期之前增加,而平均相关性在复苏之前达到峰值。人们很容易得出这样的结论:引导其他股票的股票(stalke,引导者)要对跟随它们的股票((stalkers,跟踪者)崩盘负责。然而,这个结论有一个逻辑上的缺口:我们仍然没有建立起跟踪者和跟踪者之间的因果关系。为了避免这种由事后数据发现的研究结论,似乎有必要分析潜在变量与财务变量之间的关系。
但我们进一步思考,潜在变量是由一个非线性过程描述的,它们与链路概率的关系也是非线性的。这说明:
1)如果潜在变量与财务变量之间的关系是线性的,那么财务变量与股票收益之间就不可能是线性的;
2)如果财务变量与股票收益呈线性相关,则财务变量与潜在变量之间不可能存在线性关系;
3)财务变量与潜在变量之间不存在联系。
虽然第三种可能性也有可能发生,但我们在这里先忽略它。我们可以对前两种可能性做出更有意义的评论。为了计算方便,通常在金融文献中假设财务变量和股票收益之间存在线性关系,但这种假设没有科学依据。然而,假设潜在因素和财务变量是线性相关的似乎是合理的。这也代表链路概率和财务变量之间的非线性关系。新闻和公告等因素肯定需要区别对待,修改我们的模型以包含这些因素会很有趣,可以在动态网络模型简单修改来分析危机期间新闻和公告的影响。但这些是相当费力和耗时的工作,我们将把这些研究留给未来。
参考文献
【1】Acharya, V., L. H. Pedersen, T. Philippon, and M. Richardson. 2017. “Measuring Systemic Risk.” The Review of Financial Studies 30 (1): 2–47.
【2】Adrian, T., and M. Brunnermeier. 2016. “CoVar.” American Economic Review 106 (1): 1705–1741.
【3】Ang, A., and J. Chen. 2002. “Asymmetric Correlations of Equity Portfolios.” Journal of Financial Economics 63 (3): 443–494.
【4】Billio, M., M. Getmansky, A. Lo, and L. Pelizzon. 2010. “Econometric Measures of Systemic Risk in the Finance and Insurance Sectors.” Journal of Financial Economics 104 (3): 535–559.
【5】Blei, D. M., A. Y. Ng, and M. I. Jordan. 2003. “Latent Dirichlet Allocation.” Journal of Machine Learning Research 3 (March): 993–1022.
【6】Borg, I., and P. J. F. Groenen. Modern Multidimensional Scaling. New York: Springer-Verlag. 2005.
【7】Brownlees, C., and R. F. Engle. 2017. “SRISK: A Conditional Capital Shortfall Measure of Systemic Risk.” The Review of Financial Studies 30 (1): 48–79.
【8】Cao, G., Y. Shi, and Q. Li. 2017. “Structure Characteristics of the International Stock Market Complex Network in the Perspective of Whole and Part.” Discrete Dynamics in Nature and Society Article ID: 9731219.
【9】Cappiello, L., R. F. Engle, and K. Sheppard. 2006. “Asymmetric Dynamics in the Correlations of Global Equity and Bond Returns.” Journal of Financial Econometrics 4 (4): 537572.
【10】Cox, T. F., and M. A. A. Cox. Multidimensional Scaling. Boca Raton: Chapman & Hall. 2011.
【11】Dai, A. M., C. Olah, and Q. V. Le. 2015. “Document Embedding with Paragraph Vectors.” Proceedings of the NIPS Deep Learning Workshop. arXiv preprint arXiv:1507.07998.
【12】Das, S. R. 2016. “Matrix Metrics: Network-based Systemic Risk Scoring.” The Journal of Alternative Investments 18 (4): 3351.
【13】Das, S. R., S. Kim, and D. N. Ostrov. 2019. “Dynamic Systemic Risk: Networks in Data Science.” The Journal of Financial Data Science 1 (1): 141–158.
【14】Independent Evaluation Group. 2011. “The World Bank Group’s Response to the Global Economic Crisis: Phase 1.” World Bank.
【15】Jiang, Z., and W. Zhou. 2010. “Complex Stock Trading Network among Investors.” Physica A: Statistical Mechanics and Its Applications 21 (November): 4929–4941.
【16】Kim, M., and H. Sayama. 2017. “Predicting Stock Market Movements Using Network Science: An Information Theoretic Approach.” Applied Network Science 2: 35.
【17】Kritzman, M., Y. Li, S. Page, and R. Rigobon. 2011. “Principal Components as a Measure of Systemic Risk.” The Journal of Portfolio Management 37 (4): 112–126.
【18】Li, S., Y. Yang, C. Li, L. Li, and X. Gui. 2016. “Stock Correlation Analysis Based on Complex Network.” 6th International Conference on Electronics Information and Emergency Communication, 2016.
【19】Litzenberger, R., and D. Modest. 2008. “Crisis and NonCrisis Risk in Financial
【20】Markets: A Unified Approach to Risk Management.” SSRN, https://papers.ssrn.com/sol3/papers. cfm?abstract_id=1160273.
【21】Mantegna, R. 1999. “Hierarchical Structure in Financial Markets.” The European Physical Journal B—Condensed Matter and Complex Systems 11 (1): 193–197.
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成, 在政策、市场环境发生变化时模型存在失效的风险。

往
期
链
接
注:文中报告节选自兴业证券经济与金融研究院已公开发布研究报告,具体报告内容及相关风险提示等详见完整版报告。
证券研究报告:《西学东渐--海外文献推荐系列之四十四》。
对外发布时间:2019年10月3日
报告发布机构:兴业证券股份有限公司(已获中国证监会许可的证券投资咨询业务资格)
--------------------------------------
联系人:徐寅
E-mail: xuyinsh@xyzq.com.cn
--------------------------------------
联系人:郑兆磊
微信:13918491550
E-mail: zhengzhaolei@xyzq.com.cn
--------------------------------------
以上是关于如何确定股票的联动效应?基于网络模型的择时研究的主要内容,如果未能解决你的问题,请参考以下文章