构建神经网络模型

Posted 2021-04-07 传说中的陈小黑

波士顿房价预测是一个经典的机器学习任务，类似于程序员世界的“Hello World”。和大家对房价的普遍认知相同，波士顿地区的房价是由诸多因素影响的。该数据集统计了13种可能影响房价的因素和该类型房屋的均价，期望构建一个基于13个因素进行房价预测的模型

对于预测问题，可以根据预测输出的类型是连续的实数值，还是离散的标签，区分为回归任务和分类任务。因为房价是一个连续值，所以房价预测显然是一个回归任务。

假设房价和各影响因素之间能够用线性关系来描述：

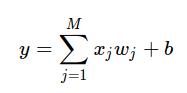
模型的求解即是通过数据拟合出每个w和b。其中，w和b分别表示该线性模型的权重(weight)和偏置(bias)。

线性回归模型使用均方误差作为损失函数（Loss），用以衡量预测房价和真实房价的差异

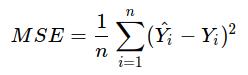
这里我们仅用一层且只有一个神经元的简单神经网络实现.

数据处理

数据处理包含五个部分：数据导入、数据形状变换、数据集划分、数据归一化处理和封装load_data函数。数据预处理后并传入，才能被模型调用。

模型设计

模型设计是深度学习模型关键要素之一，也称为网络结构设计，相当于模型的假设空间，即实现模型“前向计算”（从输入到输出）的过程。

如果将输入特征和输出预测值均以向量表示，输入特征x有13个分量，y有1个分量，那么参数权重的形状（shape）是13×1

训练配置

模型设计完成后，需要通过训练配置寻找模型的最优值，即通过损失函数来衡量模型的好坏。

我们需要有某种指标来衡量预测值z(y-hat)跟真实值y之间的差距。对于回归问题，最常采用的衡量方法是使用均方误差作为评价模型好坏的指标

训练过程

接下来介绍如何求解参数w和b的数值，这个过程也称为模型训练过程。训练过程是深度学习模型的关键要素之一，其目标是让定义的损失函数Loss尽可能的小，也就是说找到一个参数解w和b使得损失函数取得极小值。

基于微积分知识，求一条曲线在某个点的斜率等于函数该点的导数值。那么大家思考下，当处于曲线的极值点时，该点的斜率是为0,即该函数在极值点处的导数为0. 但如果模型中含有非线性变换，或者损失函数不是均方差这种简单的形式，则很难通过求解导函数为0的点来求解极值点。

梯度下降法 gradient

这种情况特别类似于一位想从山峰走到坡谷的盲人，他看不见坡谷在哪（无法逆向求解出Loss导数为0时的参数值），但可以伸脚探索身边的坡度（当前点的导数值，也称为梯度）。那么，求解Loss函数最小值可以“从当前的参数取值，一步步的按照下坡的方向下降，直到走到最低点”实现。

通过微积分中的链式法则, 我们很容易能算出L对w和对b的偏导数,因此可以推导后列出计算梯度的公式,代入数据计算即得到梯度

更新梯度 update

只需要让参数w和b沿着梯度反方向走一小步(减小一点点)，损失函数的值就减小了

做输入特征的归一化，保持尺度一致是为了让统一的步长/学习率更加合适。

特征输入未归一化时，不同特征对应的参数所需的步长不一致，尺度较大的参数需要大步长，尺寸较小的参数需要小步长，导致无法设置统一的学习率。

补充: 

选用均方差作为损失函数的好处：

曲线的最低点是可导的。

越接近最低点，曲线的坡度逐渐放缓，有助与基于当前的梯度来判断接近最低点的程度（是否逐渐减少步长，以免错过最低点）。

而这两个特性绝对值误差是不具备的，这也是损失函数的设计不仅仅要考虑“合理性”，还要追求“易解性”的原因。

随机梯度下降（SGD）

每次损失函数和梯度计算都是基于数据集中的全量数据, 如果每次都使用全部的数据，效率非常低

一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体，基于这部分数据计算梯度和损失来更新参数.这种方法叫做被称作随机梯度下降法（Stochastic Gradient Descent，SGD）

min-batch：每次迭代时抽取出来的一批数据被称为一个min-batch。

batch_size：一个mini-batch所包含的样本数目称为batch_size。

epoch：当程序迭代的时候，按mini-batch逐渐抽取出样本，当把整个数据集都遍历到了的时候，则完成了一轮的训练，也叫一个epoch。启动训练时，可以将训练的轮数num_epochs和batch_size作为参数传入。

按此方法不断的取出新的mini-batch，并逐渐更新网络参数

训练过程代码修改

将每个随机抽取的mini-batch数据输入到模型中用于参数训练。训练过程的核心是两层循环：

第一层循环，代表样本集合要被训练遍历几次，称为“epoch”，代码如下：

for epoch_id in range(num_epoches):

第二层循环，代表每次遍历时，样本集合被拆分成的多个批次，需要全部执行训练，称为“iter (iteration)”，

代码如下：for iter_id,mini_batch in emumerate(mini_batches):

在两层循环的内部是经典的四步训练流程：前向计算->计算损失->计算梯度->更新参数

另外，我们这里是按顺序取出mini_batch的，而SGD里面是随机的抽取一部分样本代表总体。为了实现随机抽样的效果，我们先将train_data里面的样本顺序随机打乱，然后再抽取mini_batch。随机打乱样本顺序，需要用到np.random.shuffle()函数

# data.py
def load_data(): # 数据导入 datafile = './work/housing.data' data = np.fromfile(datafile, sep=' ')
 # 矩阵变换 feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV'] feature_num = len(feature_names) data = data.reshape([data.shape[0] // feature_num, feature_num])
 # 数据集划分和归一化处理 ratio = 0.8 offset = int(data.shape[0] * ratio) training_data = data[:offset] maximums, minimums, avgs =  training_data.max(axis=0),  training_data.min(axis=0),  training_data.sum(axis=0) / training_data.shape[0] for i in range(feature_num): # 归一化处理 data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i]) training_data = data[:offset] # 数据集划分 test_data = data[offset:] return training_data, test_data # 返回训练集数据和测试集数据

# network.py
import numpy as np
class Network(object): def __init__(self, num_of_weights): # 随机产生w的初始值 # 为了每次运行结果的一致性 # 这里设置固定的随机数种子 np.random.seed(0) self.w = np.random.randn(num_of_weights, 1) # self.w[5] = -100 # self.w[9] = -100 self.b = 0
 def forward(self, x): z = np.dot(x, self.w) + self.b return z
 def loss(self, z, y): error = z - y num_samples = error.shape[0] cost = error * error cost = np.sum(cost) / num_samples return cost
 def gradient(self, x, y): z = self.forward(x) gradient_w = (z - y) * x gradient_w = np.mean(gradient_w, axis=0) gradient_w = gradient_w[:, np.newaxis] gradient_b = z - y gradient_b = np.mean(gradient_b, axis=0) return gradient_w, gradient_b
 def update(self, gradient_w, gradient_b, eta=0.01): # self.w[5] = self.w[5] - eta * gradient_w5 # self.w[9] = self.w[9] - eta * gradient_w9 self.w = self.w - eta * gradient_w self.b = self.b - eta * gradient_b
 def train(self, training_data, num_epoches, batch_size, eta=0.01): n = len(training_data) losses = [] for epoch_id in range(num_epoches): np.random.shuffle(training_data) mini_batches = [training_data[k: k + batch_size] for k in range(0, n, batch_size)] for iter_id, mini_batch in enumerate(mini_batches): x = mini_batch[:, : -1] y = mini_batch[:, -1:] a = self.forward(x) loss = self.loss(a, y) gradient_w, gradient_b = self.gradient(x, y) self.update(gradient_w, gradient_b, eta) losses.append(loss) print('Epoch {:3d} / iter {:3d}, loss = {:.4f}' .format(epoch_id, iter_id, loss)) return losses

# train.pyimport datafrom network import *import matplotlib.pyplot as plt
# 获取数据train_data, test_data = data.load_data()
# 创建网络net = Network(13)# 启动训练losses = net.train(train_data, num_epoches=100, batch_size=101, eta=0.10)
# 画出损失函数的变化趋势plot_x = np.arange(len(losses))plot_y = np.array(losses)plt.plot(plot_x, plot_y)plt.show()