防止神经网络模型过拟合的6种方法及keras代码实现

Posted 2021-04-07 深度学习社区DLC

最近这段时间，有网友问我，自己的模型存在过拟合问题，就是模型其实训练的已经很好了，但是在测试集上的表现性能不佳。这些常见的模型比如卷积神经网络、循环神经网络、自编码器等等。

这种在训练集上表现的好，在测试集上效果差，模型泛化能力弱，则是典型的过拟合问题。下面将结合实际介绍几种解决过拟合的方法。

过拟合问题

由于模型过于复杂，学习能力过强，而用于训练的数据相对于复杂模型来说比较简单，所有模型会去学习数据中隐含的噪声，导致模型学不到真正数据集的分布，如下图所示，红色线就是由于模型过分的拟合了训练数据集，导致泛化能力过差。而蓝色线才是真正的数据集的分布。

同时，在很多问题上，我们无法穷尽所有状态，不可能将所有情况都包含在训练集上。所以，必须要解决过拟合问题。

解决过拟合的方法

1.获取更多的数据

这是解决过拟合最有效的方法，只要给足够多的数据，让模型「看见」尽可能多的「例外情况」，它就会不断修正自己，从而得到更好的结果：

如何获取更多数据，可以有以下几个方法：
从数据源头获取更多数据：这个是容易想到的，例如物体分类，我就再多拍几张照片好了；但是，在很多情况下，大幅增加数据本身就不容易；另外，我们不清楚获取多少数据才算够；
根据当前数据集估计数据分布参数，使用该分布产生更多数据：这个一般不用，因为估计分布参数的过程也会代入抽样误差。
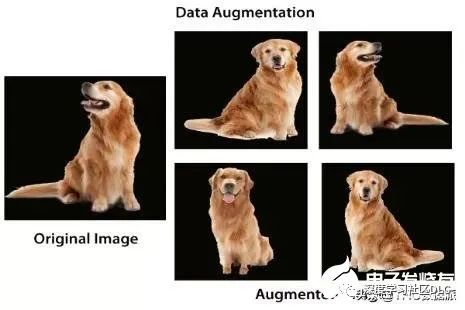
数据增强（Data Augmentation）：通过一定规则扩充数据，往往应用在图像领域。如在物体分类问题里，物体在图像中的位置、姿态、尺度，整体图片明暗度等都不会影响分类结果。我们就可以通过图像平移、翻转、缩放、切割等手段将数据库成倍扩充；在神经网络中，数据增强意味着增加数据规模，也就是增加数据集里中图像的数量。数据增强例子如下：

 

2.选择合适的网络结构

过拟合主要是有两个原因造成的：数据太少+模型太复杂。所以，我们可以通过使用合适复杂度的模型来防止过拟合问题，让其足够拟合真正的规则，同时又不至于拟合太多抽样误差。

例如：RNN-->（IndRNN)、LSTM-->GRU;CNN-->fastCNN-->Unet等；

3.Dropout

3.1 Dropout原理

Dropout正则化是最简单的神经网络正则化方法。它不改变网络本身，而是随机地删除网络中的一般隐藏的神经元，并且让输入层和输出层的神经元保持不变。每次使用梯度下降时，只使用随机的一般神经元进行更新权值和偏置，因此我们的神经网络是在一半的隐藏神经元被丢弃的情况下学习的。可以理解为，当dropout不同神经元集合时，有点像在训练不同的神经网络。而不同的神经网络会以不同的方式过拟合，所以dropout就类似于不同的神经网络以投票的方式降低过拟合。其原理如图右边所示。

 

3.2   Dropout代码实现

dropout函数实现 ：

  
    
    
  
 
   
#dropout函数实现
 
   
def dropout(x, level): # level为神经元丢弃的概率值，在0-1之间
 
   
if level < 0. or level >= 1:
 
   
raise Exception('Dropout level must be in interval [0, 1[.')
 
   
retain_prob = 1. - level
 
   
 # 利用binomial函数，生成与x一样的维数向量。
 
   
 # 神经元x保留的概率为p，n表示每个神经元参与随机实验的次数，通常为1,。
 
   
 # size是神经元总数。
 
   
sample=np.random.binomial(n=1,p=retain_prob,size=x.shape)
 
   
 # 生成一个0、1分布的向量，0表示该神经元被丢弃
 
   
 # print sample
 
   
x *=sample
 
   
 # print x
 
   
x /= retain_prob
 
   
return x
 
  

keras实现dropout：

Dropout可以应用于两个隐藏层之间以及最后一个隐藏层和输出层之间，例如：

  
    
    
  
 
   
model.add(Embedding(top_words, embedding_vecor_length, input_length=max_review_length))
 
   
model.add(Dropout(0.2))
 
   
model.add(LSTM(100))
 
   
model.add(Dropout(0.2))
 
  

Dropout可以应用于LSTM、GRU等神经网络中，例如：

model.add(layers.GRU(128, dropout=0.5, input_shape=(None, 4),recurrent_dropout=0.5,kernel_regularizer=regularizers.l2(0.01)))

keras.layers.recurrent.LSTM(output_dim, init='glorot_uniform', inner_init='orthogonal', forget_bias_init='one', activation='tanh', inner_activation='hard_sigmoid', W_regularizer=None, U_regularizer=None, b_regularizer=None, dropout_W=0.0, dropout_U=0.0)

 其中：

output_dim：内部投影和输出的维度
init：初始化方法，为预定义初始化方法名的字符串，或用于初始化权重的Theano函数。
inner_init：内部单元的初始化方法
forget_bias_init：遗忘门偏置的初始化函数，Jozefowicz et al.建议初始化为全1元素
activation：激活函数，为预定义的激活函数名（参考激活函数）
inner_activation：内部单元激活函数
W_regularizer：施加在权重上的正则项，为WeightRegularizer对象
U_regularizer：施加在递归权重上的正则项，为WeightRegularizer对象
b_regularizer：施加在偏置向量上的正则项，为WeightRegularizer对象
dropout_W：0~1之间的浮点数，控制输入单元到输入门的连接断开比例
dropout_U：0~1之间的浮点数，控制输入单元到递归连接的断开比例

4. Early stopping

4.1 Early stopping原理

为了获得性能良好的神经网络，网络定型过程中需要进行许多关于所用设置（超参数）的决策。超参数之一是定型周期（epoch）的数量：亦即应当完整遍历数据集多少次（一次为一个epoch）？如果epoch数量太少，网络有可能发生欠拟合（即对于定型数据的学习不够充分）；如果epoch数量太多，则有可能发生过拟合（即网络对定型数据中的“噪声”而非信号拟合）。

早停法旨在解决epoch数量需要手动设置的问题。它也可以被视为一种能够避免网络发生过拟合的正则化方法（与L1/L2权重衰减和丢弃法类似）。而Early stopping的原理就是在每个epoch结束后（或每N个epoch后)：在验证集上获取测试结果，随着epoch的增加，如果在验证集上发现测试误差上升，则停止训练；将停止之后的权重作为网络的最终参数。其原理可以解释为如图所示。

4.2 Early stopping代码实现

keras代码实现：

  
    
    
  
 
   
import keras
 
   
early_stopping=keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=0,
 
   
patience=0, verbose=0, mode='auto',
 
   
baseline=None, restore_best_weights=False)
 
   
model.fit(X_train_pre, y_train_pre, batch_size=512,validation_data=(X_train_pre_val, y_train_pre_val)epochs=500,callbacks = [early_stopping])
 
  

其中：
monitor: 被监测的数据。
min_delta: 在被监测的数据中被认为是提升的最小变化， 例如，小于 min_delta 的绝对变化会被认为没有提升。
patience: 没有进步的训练轮数，在这之后训练就会被停止。
verbose: 详细信息模式。
mode: {auto, min, max} 其中之一。在 min 模式中， 当被监测的数据停止下降，训练就会停止；在 max 模式中，当被监测的数据停止上升，训练就会停止；在 auto 模式中，方向会自动从被监测的数据的名字中判断出来。
baseline: 要监控的数量的基准值。如果模型没有显示基准的改善，训练将停止。
restore_best_weights: 是否从具有监测数量的最佳值的时期恢复模型权重。如果为 False，则使用在训练的最后一步获得的模型权重。

5. 正则化

5.1 参数正则化原理

正则化是一种回归的形式，它将系数估计（coefficient estimate）朝零的方向进行约束、调整或缩小。也就是说，正则化可以在学习过程中降低模型复杂度和不稳定程度，从而避免过拟合的危险。总的来说正则化通过降低模型的复杂性， 达到避免过拟合的问题。常见的正则方法有L1正则和L2正则。

L2 regularizer ：使得模型的解偏向于范数较小的 W，通过限制 W 范数的大小实现了对模型空间的限制，从而在一定程度上避免了过拟合（因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是『抗扰动能力强』） 。不过 ridge regression 并不具有产生稀疏解的能力，得到的系数仍然需要数据中的所有特征才能计算预测结果，从计算量上来说并没有得到改观。
L1 regularizer ：它的优良性质是能产生稀疏性，导致 W 中许多项变成零。稀疏的解除了计算量上的好处之外，更重要的是更具有“可解释性”。

5.2 keras 实现L1和L2正则化

keras的某一层使用正则化：

  
    
    
  
 
   
from keras import regularizers
 
   
model.add(Dense(64, input_dim=64,
 
   
kernel_regularizer=regularizers.l2(0.01),
 
   
activity_regularizer=regularizers.l1(0.01)))
 
  

其中常用的正则化方法：（大家可以替换上述代码中的方法）
keras.regularizers.l1(0.01)
keras.regularizers.l2(0.01)
keras.regularizers.l1_l2(l1=0.01, l2=0.01)

然后你也可以通过keras的backend函数改写新的正则化方法。代码例如：

  
    
    
  
 
   
from keras import backend as K
 
   
def l1_reg(weight_matrix):
 
   
    return 0.01 * K.sum(K.abs(weight_matrix))
 
   
model.add(Dense(64, input_dim=64,
 
   
                kernel_regularizer=l1_reg))
 
  

6. batch normallization

6.1 batch normallization原理

batch normalization 就是对数据做批规范化，使得数据满足均值为0,方差为1的正太分布。其主要作用是缓解DNN训练中的梯度消失/爆炸现象，加快模型的训练速度。

其原因是：机器学习领域有个很重要的假设：IID独立同分布假设，就是假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。但是在深层神经网络中，每轮迭代后基本上所有的网络的参数都会更新，所以就导致在训练过程中，每一个隐藏层的输入分布总是变来变去的，并且随着网络层数加深，更深层的隐藏层网络的输入分布差异会更大，这就是所谓的“Internal Covariate Shift”现象，为了解决这一现象，论文（1）中提出了Batch Normalization(BN)的基本思想：让每个隐藏层节点的激活输入分布固定下来。具体如何操作呢？就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样把输入的分布变窄(固定在[-1,1])，但是让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

BN的优点：
①极大提升了训练速度，收敛过程大大加快；
②增加了分类效果，一种解释是这是类似于Dropout的一种防止过拟合的正则化表达方式，所以不用Dropout或正则化也能达到相当的效果；
③简化了调参过程，对于初始化参数权重不太敏感，允许使用较大的学习率

6.2 batch normallization代码实现

batch normallization函数：

keras.layers.normalization.BatchNormalization(axis=-1, momentum=0.99, epsilon=0.001, center=True, scale=True, beta_initializer='zeros', gamma_initializer='ones', moving_mean_initializer='zeros', moving_variance_initializer='ones', beta_regularizer=None, gamma_regularizer=None, beta_constraint=None, gamma_constraint=None)

其中：

epsilon：大于0的小浮点数，用于防止除0错误
mode：整数，指定规范化的模式，取0或1
0：按特征规范化，输入的各个特征图将独立被规范化。规范化的轴由参数axis指定。注意，如果输入是‘th’格式形状的（samples，channels，rows，cols）的4D图像张量，则应设置规范化的轴为1，即沿着通道轴规范化。在训练阶段，我们使用每个batch数据的统计信息（如：均值、标准差等）来对训练数据进行规范化，而在测试阶段，我们使用训练时得到的统计信息的滑动平均来对测试数据进行规范化。
1：按样本规范化，该模式默认输入为2D
2: 按特征规范化, 与模式0相似, 但不同之处在于：在训练和测试过程中，均使用每个batch数据的统计信息而分别对训练数据和测试数据进行规范化。
axis：整数，指定当mode=0时规范化的轴。例如输入是形如（samples，channels，rows，cols）的4D图像张量，则应设置规范化的轴为1，意味着对每个特征图进行规范化
momentum：在按特征规范化时，计算数据的指数平均数和标准差时的动量
weights：初始化权重，为包含2个numpy array的list，其shape为[(input_shape,),(input_shape)]
beta_init：beta的初始化方法，为预定义初始化方法名的字符串，或用于初始化权重的Theano函数。该参数仅在不传递weights参数时有意义。
gamma_init：gamma的初始化方法，为预定义初始化方法名的字符串，或用于初始化权重的Theano函数。该参数仅在不传递weights参数时有意义。
gamma_regularizer：WeightRegularizer(如L1或L2正则化)的实例，作用在gamma向量上。
beta_regularizer：WeightRegularizer的实例，作用在beta向量上。

keras实现的模型调用batch normallization函数：

  
    
    
  
 
   
# import BatchNormalization
 
   
from keras.layers.normalization import BatchNormalization
 
   
# instantiate model
 
   
model = Sequential()
 
   
# we can think of this chunk as the input layer
 
   
model.add(Dense(64, input_dim=14, init='uniform'))
 
   
model.add(BatchNormalization())
 
   
model.add(Activation('tanh'))
 
   
model.add(Dropout(0.5))
 
   
# setting up the optimization of our weights
 
   
sgd = SGD(lr=0.1, decay=1e-6, momentum=0.9, nesterov=True)
 
   
model.compile(loss='binary_crossentropy', optimizer=sgd)
 
   
# running the fitting
 
   
model.fit(X_train, y_train, nb_epoch=20, batch_size=16, show_accuracy=True, validation_split=0.2, verbose = 2)
 
  

总结

针对神经网络方法在建模中存在的"过拟合"(overfitting)现象和提高泛化性能 (generalizationcapability)问题。本文基于此需求介绍了几种解决过拟合的实际方法。这几种方法有效地解决了在神经网络学习过程中的过拟合问题 ,提高了网络的适应性。

参考文献：

1.Ioffe S , Szegedy C . Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift[J]. 2015.

2.Srivastava N , Hinton G , Krizhevsky A , et al. Dropout: A Simple Way to Prevent Neural Networks from Overfitting[J]. Journal of Machine Learning Research, 2014, 15(1):1929-1958.

3.https://keras-cn.readthedocs.io/en/latest/

4.Song H , Kim M , Park D , et al. How does Early Stopping Help Generalization against Label Noise?[C]// International Conference on Machine Learning, Workshop on Uncertainty and Robustness in Deep Learning (UDL). arXiv, 2019.

5.鞠维欣, 赵希梅, 魏宾,等. Cirrhosis Recognition by Deep Learning Model GoolgeNet-PNN[J]. 计算机工程与应用, 2019, 055(005):112-117.