文献阅读通过神经网络模型理解大脑中的时间信息处理过程

Posted 2021-04-07 动态世界观

导语

时间信息对大脑执行各种任务都至关重要，但我们对大脑处理时间的机制仍不甚明确。本文通过建立计算模型，分析模型在任务中处理时间信息的方式，以此来类推大脑处理时间信息的原理。在此模型中，观测到了一部分与小鼠实验结果一致的现象，说明计算模型与大脑二者之间确实存在一定的相似性。

本文主要聚集于以下三个问题进行分析：

1.大脑如何感知、保存、复现关于时间间隔的信息？

2.与时间有关的信息在大脑中如何与其他信息一同存储？

3.在许多不需要时间信息的任务中，实验上仍能观察到很强的时间信号，如何解释这一现象？

模型结构

本文采用的模型为单隐层的循环神经网络（RNN），循环层单元数为256，激活函数为sigmoid函数。为强化循环层的自联结，循环矩阵对角项被初始化为1，其他项则随机初始化。为防止过拟合，在任务正确率达到95%时即终止训练过程。

为防止单个模型的特殊性，对提到的每个分析，本文均采用了不同初始参数训练了若干模型，对这些模型的结果进行了统计检验。

训练任务

为观察模型中与时间有关的效应，本文提出了4个与时间相关的任务。对每个不同的任务，分别初始化模型进行训练。任务如下：

1.间隔复现（IP）：先输入两个信号脉冲，模型需要记住两次脉冲之间的时间间隔；而后在一段随机时间后，输入一个提示脉冲。模型需要在接收到提示脉冲之后，等待与之前两次信号脉冲间隔相同长度的时间，而后产生一个脉冲作为输出。

2.间隔比较（IC）：先输入一段持续一定时长的信号，而后在随机间隔后再输入另一段信号，模型需要在第二段信号结束后判断哪一段信号持续时长更长。

3.间隔-位置复现（t-SR）：先输入两个信号脉冲，而此时第一个脉冲包含空间位置的信息（用一个高斯波包表示）。模型需要记住第一个脉冲的位置和两次脉冲之间的时间间隔；而后在一段随机时间后，输入一个提示脉冲。模型需要在接收到提示脉冲之后，等待与之前两次信号脉冲间隔相同长度的时间，而后产生一个脉冲作为输出，输出位置要求和第一个脉冲相同。

4.保持间隔并比较强度（t-DM）：同时输入两段持续时长一致的含噪声信号，二者均值强度不同。模型需要记住信号持续时长，并判断二者高低。一段随机时间后，输入一个提示脉冲。模型需要在接收到提示脉冲之后，等待与之前信号持续时长相同长度的时间，而后判断两个信号何者更强。

可以看出，前两个任务均为纯时间任务，而后两个任务在处理时间信息外，还需对空间位置或刺激强度信息做出处理。

图1 任务示意图

模型分析

在对模型训练完毕后，提取循环层每个时刻的激活情况进行分析。由于在循环神经网络中，循环层的每个单元近似等效于模拟大脑中的一个神经元，因此每个时刻的激活情况实质上等效于模拟神经元的发放强度，而在每个时刻，256个“神经元”各有一个发放强度。

由于全部的发放强度实际构成一个256维度的向量，而高维度的向量很难处理和直观理解，因此我们首先使用主成分分析（PCA）对每个时间点的发放向量进行降维变换。此时只需要变换后的前几个维度，即可较好的描述整体的发放情况。

由于每个任务的内容不同，分析的着眼点也不甚一致，我们将对四个任务的数据分别进行分析：

IP任务

任务可以分为三个阶段：接受刺激，保持刺激，复现刺激，在三个阶段中由于需要进行的工作不一样，循环层的行为也有所不同，此处分别进行分析：

1.接受刺激

在此阶段中，模型需要在接收到第一个刺激之后开始计时，而在第二个刺激到来时停止计时。由于模型无法预先预测第二个刺激到来的时间，模型在接受到第一个刺激后，内部发放情况应当持续发生变化，以表征不断增加的时间间隔。这种变化也应当在主成分上体现出来，因此可以用模型在前三个主成分（PC）组成的三维空间中的轨迹来表征模型内部的大致发放情况。

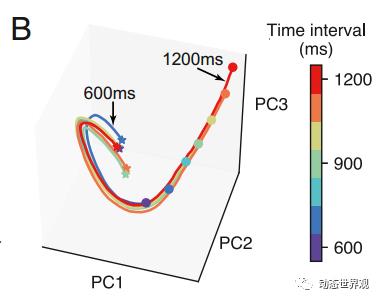
图2  IP任务接受刺激阶段时的发放轨迹，线条的颜色代表两个信号刺激之间的间隔，五角星标记为第一个信号刺激，圆圈标记为第二个信号刺激。

可以看出，在第二个刺激到来前，模型的发放沿着一条固定轨迹（Stereotypical Trajectory）不断行进，而由于第二个刺激到来的时间不同，此阶段结束时模型在空间中所处的位置也不同，结束时刻的位置实际上就是对时间间隔的一种表征。

2.保持刺激

上一阶段中，结束时刻模型发放状态所处的位置提供了对信号间隔的一种表征，但系统是如何将这一表征持续保存于模型之中的呢？这个问题的答案，需要从保持阶段的发放轨迹中寻找：

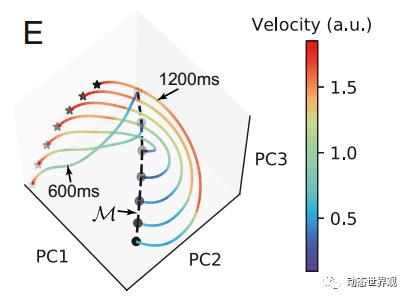
图3 IP任务保持阶段的发放轨迹，不同的线代表不同信号间隔时长，由左下到右上分别为600ms-1200ms。线条的颜色代表空间中的瞬时速度，五角星标记代表阶段起始点（第二个信号刺激），圆圈标记代表阶段结束点（提示刺激）

在图中可以看出，保存了不同刺激信息的轨迹近似平行地在空间中分布，而在保持阶段后期，这些点近似落在了同一条直线上（图中的虚线M），且其位置基本随保持的间隔长度而线性排布，这一点在进一步的分析中得到了证实：

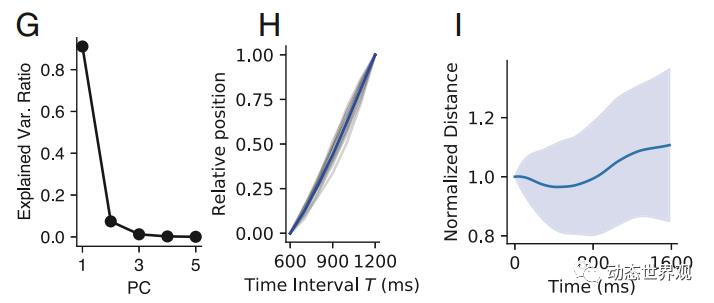
图4  对M上各点的分析。G图：对各点进行PCA降维，发现只需第一个维度即可很好描述各点分布，说明各点近似共线。H图：保存的时间间隔与轨迹点在M上相对位置的关系图，二者线性相关。I图：相邻两点之间距离随保持时长的变化，距离基本保持稳定，说明这种线性相关具有稳定性。

这种路径点始终保持共线的情形，被称为“线性吸引子”（Linear Attractor）。由以上分析我们可以得出，时间间隔信息的保持正是借助了这样的“线性吸引子”：前一阶段中接收到的时间间隔的大小，在这一阶段被编码为了吸引子M上的位置。

3.复现刺激

仅是将刺激信息存储进内部是不够的，模型还需要有能力复现给定的时间间隔。在这一阶段的轨迹图中，我们可以看到，模型采取了与前两阶段截然不同的策略：

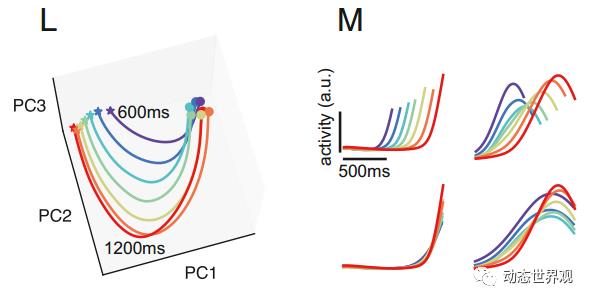
图5  IP任务复现阶段的发放轨迹。L图：在主成分空间中的轨迹，不同颜色代表储存的不同时间间隔长度，五角星标记为起始点，圆圈标记为结束点。M图：上：单个循环层单元（“神经元”）的发放情况，左右为两个不同单元。下：将上图发放序列在时间上拉伸对齐后的结果。

可以看出，不同时间间隔的试次中，虽然在此阶段中经历的时长不同，轨迹长度也不同，但整体的轨迹形状却十分相似。而如果将神经元的发放在时间上拉伸对齐，可以看出每个神经元在不同试次下的发放规律十分相似。这种现象被称之为时间上的缩放（Temporal Scaling），可以将其理解为系统每次都是经历了一个相似的过程，但存储的时间越长，这个过程的进展就越慢，相对的完成整个过程的时间也越长，藉此来复现存储的时间。

IC任务

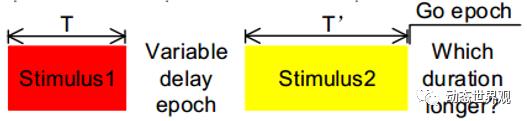
虽然此任务形式上与IP任务差异较大，但在此任务中仍然观测到了与IP任务基本一致的现象：

1.在第一个刺激持续的时间内，模型中出现了固定轨迹（Stereotypical Trajectory）的现象。

2.在两个刺激间隔的时间内，模型利用了线性吸引子（Linear Attractor）来对第一个刺激的时长进行编码。

3.在第二个刺激到来后，模型中也出现了时间缩放（Temporal Scaling）的特征，而缩放的时长基于的是第一个刺激的时长。

为何在两个看似不同的任务中却出现了类似的行为？我们可以考虑这样一个任务策略：模型先记下了第一个刺激的时长，在第二个刺激到来时，同时对第一个刺激进行回放，比较何者先结束，即可比较出二者的时长差异。

在这样的策略下，模型在两个任务中需要做的事情其实是一致的：接收并保持一个时间间隔，并将其复现。因此看到相似的特征也是容易理解的事情。

小结1

从上述两任务中，我们得到的信息已足以让我们回答全文开头处提出的第一个问题：“大脑如何感知、保存、复现关于时间间隔的信息？”。模型利用了固定轨迹的策略来感知一段未知时长的时间间隔，间隔结束时，模型在状态空间中的位置即表征了时间间隔的长度；而在接收到时间间隔后，模型会利用一个线性的吸引子来保持对时间间隔长度的编码；最终，当需要复现此时间间隔时，模型使用时间缩放来控制复现的时长，由此来精确复现出被编码的时间间隔。

t-SR任务

前两个任务均为纯时间任务，无法对第二个问题做出回答，因此在接下来两个任务中，我们引入了时间以外的其他任务参量。在t-SR任务中，除了时间间隔的长度，模型还需要对空间位置进行记忆：

由于在时间间隔记忆方面，此任务与IP任务完全一致，因此模型内部依然体现出了前面所提到的固定轨迹、线性吸引子、时间缩放三种现象。而我们此时除了时间信息的编码以外，更关心的是对空间位置的编码，以及二者之间的关系。

为了分析信息是如何通过单元发放的状态进行编码的，本文分别考虑了三种会影响模型在状态空间中位置的因素：

1.模型内部存储的时间间隔长度（Interval，下文用I代指）

2.模型内部存储的空间位置（Space，下文用S代指）

3.在一次任务中，此时所处的时间片位置（Time Flow，下文用F代指）

在考虑一个因素影响的时候，本文对另外两个因素做平均化处理，再进行PCA降维，此时提取出来的第一个维度则是此因素造成影响的最主要维度，这即意味着，系统在这个维度上的值某种程度上即反映了这个因素的大小。而用于编码这三个量维度之间的关系，即反映了模型之间储存不同信息的方式：

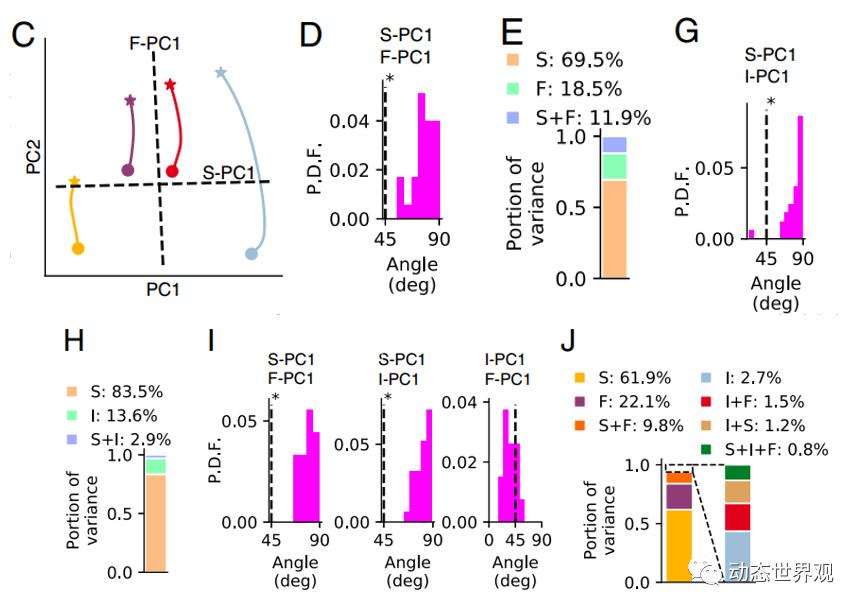
图6  各编码维度之间的关系图 C图：接受刺激阶段中，模型的F-PC1（表征F信息的第一个主成分，其余同理）和S-PC1的方向示意图，不同颜色的线条代表不同的空间位置，五角星标记和圆圈标记分别表示阶段的开始和结束。D图：接受刺激阶段中，S-PC1和F-PC1的夹角关系。E图：接受刺激阶段中，S-PC1和F-PC1对于方差的解释率。G图：保持刺激阶段中，S-PC1和I-PC1的夹角关系。H图：保持刺激阶段中，S-PC1和I-PC1对于方差的解释率。I图：复现刺激阶段中，S-PC1、F-PC1和I-PC1的夹角关系。H图：复现刺激阶段中，S-PC1、F-PC1和I-PC1对于方差的解释率。

注：由于接受刺激阶段中还未形成时间间隔信息，而保持刺激阶段中需要稳定保持刺激信息而忽略具体时间点信息，在对应阶段中排除掉了这二者的分析。

可以看出，除了在复现刺激时，时间间隔时长信息和描述时间流动的信息二者不相正交以外，参与分析的量均体现出了两个特征：（1）表征维度相互正交。（2）混合方差远小于自身的方差。（混合方差指的是在总方差中减去每个维度上的方差大小后剩余的部分，描述的是两个维度之间的相关性）

这两个特征可用下图来直观理解：

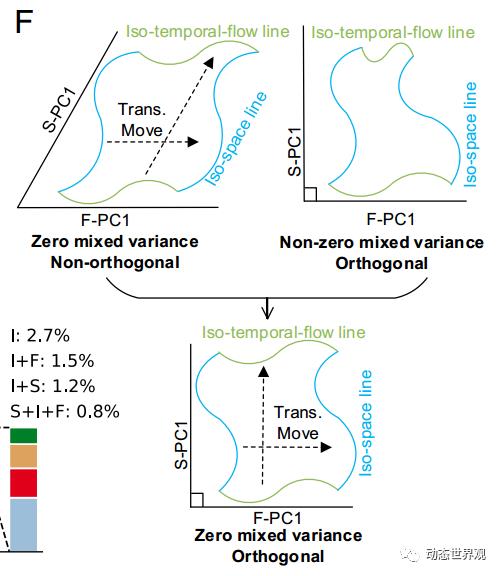
图7  维度正交与零混合方差的示意图 左上：混合方差为零但不正交 右上：正交但混合方差不为零 下：正交且混合方差为零

可以看出，只有当两维度正交且混合方差为零时，这两个维度才是独立进行表征的。在模型中，这一条件得到了满足，正意味着在不同的阶段中，时间信息和空间信息均采用的是这样一种独立的表征方式。而在刺激复现阶段中所看到的I-PC1和F-PC1二者不再正交，则正与此阶段中的复现过程有关。由于复现的时间间隔长度需要通过时间的流逝来表达，二者不再独立，因此在模型内部的表征也不再正交化。

 t-DM任务

此任务从任务设计上与上一任务基本一致，只是在感知刺激的阶段中，非时间信息由空间位置（Space）变成了对强度的决策判断（Decision，下文用D表示）。而对模型的分析也显示，其特征与上一任务基本一致。

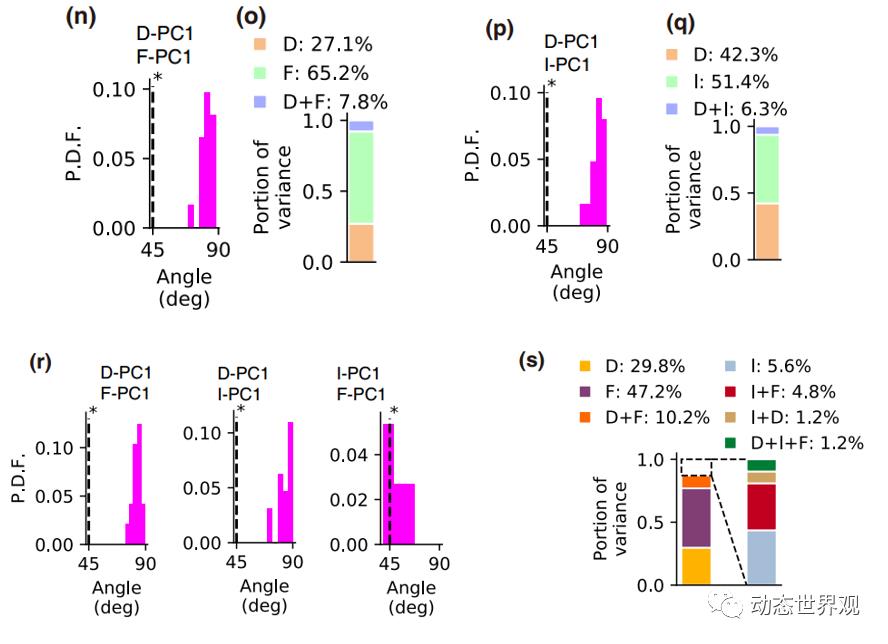
图8  t-DM任务，图中各标识与图七中一致，左上、右上和下方分别代表接受刺激，保持刺激，复现刺激三个阶段。

小结2

从这两个任务的分析中，我们可以得到回答第二个问题的信息：“与时间有关的信息在大脑中如何与其他信息一同存储？”，从上面的分析中我们可以看到，在同时保持时间信息与非时间信息时，二者保持正交独立，这一点体现在了主维度的正交性和较小的混合方差中。当信息需要独立存储时，其编码保持正交独立，以防止不同信息之间相互干扰，而当需要通过时间流逝来表达信息时，储存的信息表征将旋转到和时间流动的表征相同的方向。

解码的可推广性

关于不同特征编码之间的正交独立性，也可以从解码的角度来理解：当大脑需要将储存的信息重新提取出来时，实际上需要进行的是一个解码过程。而若某特征的表征与其他特征正交独立，那么此特征的解码将不受其他因素影响。这时我们可以说，这种解码过程存在可推广性，即同样的解码方法可以在不同时间点，或是保存的其他特征不一致时，仍然可以推广使用而不被干扰。这一点可由下图的例子说明：

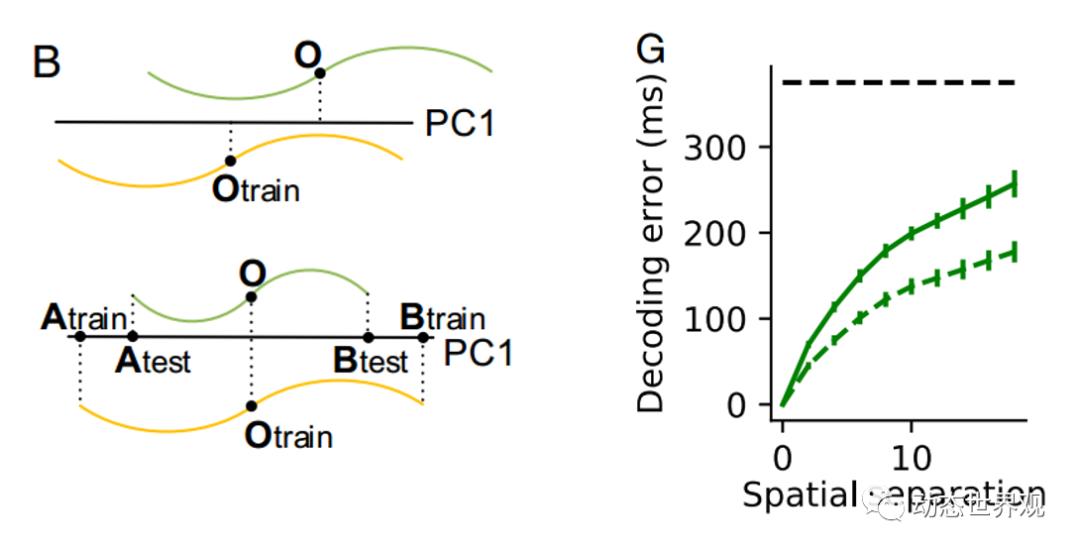
图9  编码可推广性 左图：正交和独立对编码可推广性的影响。上：独立但不正交，同一个点会投影在不同的位置。下：正交但不独立：中间的点会投影在相同位置，但两侧的点会投影在不同位置。右图：用不同空间位置（S）的表征状态进行训练，解码时间点信息（F）得到的误差分布，横轴代表训练和测试时空间位置的差异大小，两根绿色曲线为两种不同解码方式，黑色虚线代表随机水平。

我们考虑最简单的线性解码过程，解码的过程实际上是将状态空间中的点向表征特征的主轴进行投影。而由上图可以看出，只有当表征信息与其他特征的编码相互正交独立时，这一投影结果才不受其他特征的影响。实际测试时（图九右），也确实能观测到，即使使用不同空间位置的编码进行解码，解码的正确率依然优于随机水平，这说明模型内部确实存在一定的编码可推广性。

关于时间信息的进一步分析

在上面的分析中，我们基本明确了模型在四个任务中的工作机制，也借此回答了文章开头提出的前两个问题，但我们同时也发现，最后一个问题在此时体现了出来：

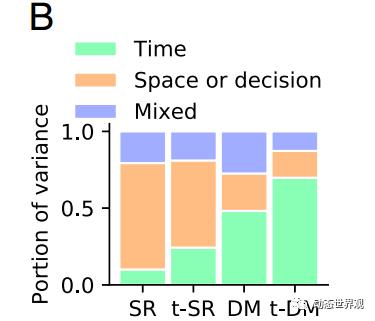
图10 四个任务中不同特征成分所解释的方差比例，绿色：时间信息，橙色：非时间信息，蓝色：混合方差

可以看到，即使在时间信息占比最多的t-DM任务中，时间信息在方差中的占比也仅有约70%，而这还是任务严重依赖于时间的特殊情形。可在实际的实验中观察到，即使是在完全无需利用时间信息的任务中，时间信息的占比也高达75%。如何解释时间信息如此高的比重？作者提出了以下四种方面的可能：

任务的时间复杂性

在t-SR任务中，只有第一个刺激携带了空间信息，因此模型在接收到第一个刺激后即可对最后的结果进行预测。若模型的反应需要与之后到来的刺激或提示有关，任务的时间复杂度就将上升，这种时间复杂度的上升或许会引起时间信息占比的上升。

为验证这一猜想，作者重新构建了五种不同的任务，为排除时间信息本身的影响，这些任务均与时间信息无关：

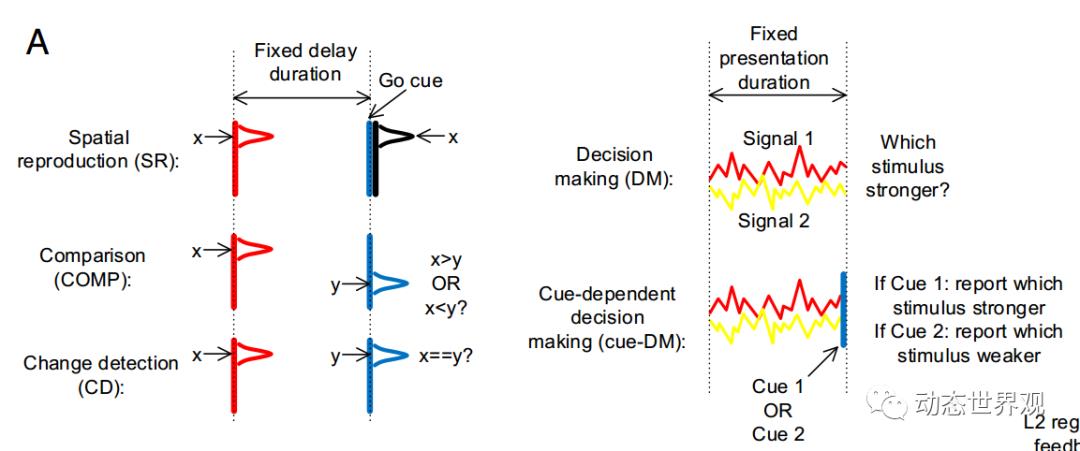
图11 任务设计

1.空间复现（SR）：第一个刺激会给出一个空间位置，在一段固定间隔后会给出一个信号刺激，模型需要立刻复现之前的空间位置。

2.空间比较（COMP）：第一个刺激会给出一个空间位置，在一段固定间隔后会给出第二个空间位置，模型需要立刻判断二者坐标的大小关系。

3.变化探测（CD）：第一个刺激会给出一个空间位置，在一段固定间隔后会给出第二个空间位置，模型需要立刻判断二者位置是否相同。

4.决策（DM）：同时输入两个固定时长的信号，在信号结束时，模型需要立刻判断何者更强。

5.带提示的决策（cue-DM）：同时输入两个固定时长的信号，在信号结束时给出一个提示，模型需要根据提示输出二者中较强的一方或较弱的一方。

将模型进行训练后可以发现，模型执行的任务时间复杂度越高，时间信息的占比也越高：

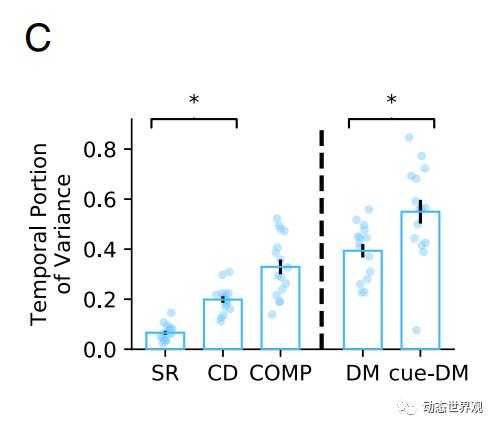
图12 不同任务的时间信息占比比较

 空间信息的重叠

在前面的空间任务中，空间位置的信息均是由空间上的一个高斯波包进行表示的。若高斯波包较宽，相邻的空间刺激之间将存在一定的重叠，导致不同空间刺激的相似度上升，进而导致空间信息在方差中的占比下降。由于占比统计的是相对大小，空间信息的占比下降，自然会导致时间信息在模型中的占比有一定的上升。

为证实这一点，作者在四个空间任务（t-SR，SR，COMP，CD）中换用了更宽的高斯波包，结果证明，这一替换将导致时间信息占比的上升：

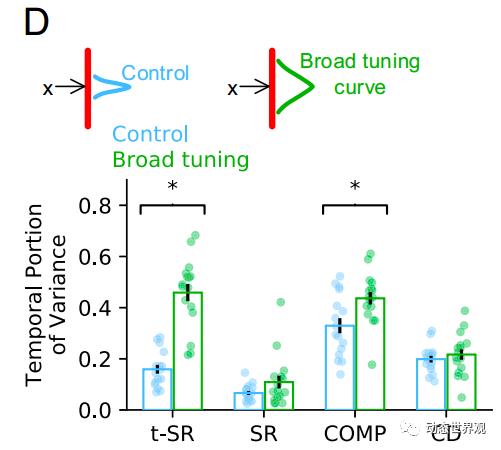
图13  空间信息重叠的影响。上：不同宽度的高斯波包 下：更换高斯波包宽度前后，不同任务的时间信息占比变化。

多任务的适应性

在本文中，对于每个不同的任务，模型都是专门化地独立进行训练。但在实际生活中，大脑往往要同时面对各种各样的任务。由于我们日常中的任务许多都与时间信息有关，这可能会对大脑造成一种惯性的影响，让我们即使在进行非时间任务时，仍然对时间信息存在强烈的表征。

为证实这个猜测，作者重新对模型进行训练，让一部分的模型同时进行时间和非时间的任务训练，并观察经过时间任务训练的模型和未经过时间任务训练的模型在非时间任务上的表现：

图14  多任务训练的影响 绿色条形图为经过对应时间任务训练的模型

可以看出，若模型经历过时间任务的训练，即使在进行非时间任务时，模型对时间信息的表征依然会有上升。

任务的时间可预期性

如果任务在时间上具有一定的规律性（例如信号刺激到来的时刻固定），则模型可能会对这些固定时刻到来的刺激有提前的预测行为，这个提前的预测行为可能也会体现为一种时间信息。

为证实这一猜测，作者将五个任务中保持阶段时长设定为固定或不固定，发现在时长固定时，时间信息的成分确实高于时长不固定的情况（图15F）。

为进一步说明这一点，考虑到预测行为可能体现为让输入单元的敏感性提升，作者在模型中引入了从循环层到输入层的反馈通路（图15G），可以发现引入反馈后，模型的时间信息确实会进一步上升（图15H），而反馈强度的变化也确实与预期的一致，在信号刺激即将到来的时候会增加输入单元的敏感程度（图15I）。

图15  时间可预期性的影响 F图：保持阶段固定或不固定对时间信息占比的影响。G图：反馈通路，反馈越强则输入层的发放阈值越低。H图：反馈通路的引入对时间信息占比的影响。I图：反馈强度随时间的变化。

小结3

以上分析给我们的第三个问题做出了一个可能的回答：这四个因素，

1.任务的时间复杂性

2.空间信息的重叠

3.多任务的适应性

4.任务的时间可预期性

可能就是在本文模型中未能考虑进去，但却影响了实际大脑，从而使得实际大脑中时间信息更高的原因。当然，可能的因素还有更多，在此处并未进行详尽的讨论，只是对几种比较可能的因素进行了分析，而这些因素也获得了一些实验证据的支持（如一些感受野较大的细胞，正对应着空间信息的一种重叠）。

总结与讨论

本文的主要内容围绕着三个关于脑中时间信息的问题展开：

1.大脑如何感知、保存、复现关于时间间隔的信息？

2.与时间有关的信息在大脑中如何与其他信息一同存储？

3.在许多不需要时间信息的任务中，实验上仍能观察到很强的时间信号，如何解释这一现象？

为回答这三个问题，作者搭建了一个循环神经网络模型，通过对网络循环层单元的激活情况分析，作者对这三个问题分别进行了回答：

1.模型利用了固定轨迹的策略来感知一段未知时长的时间间隔，间隔结束时，模型在状态空间中的位置即表征了时间间隔的长度；而在接收到时间间隔后，模型会利用一个线性的吸引子来保持对时间间隔长度的编码；最终，当需要复现此时间间隔时，模型使用时间缩放来控制复现的时长，由此来精确复现出被编码的时间间隔。

2.在同时保持时间信息与非时间信息时，二者保持正交独立，这一点体现在了主维度的正交性和较小的混合方差中。当信息需要独立存储时，其编码保持正交独立，以防止不同信息之间相互干扰，而当需要通过时间流逝来表达信息时，储存的信息表征将旋转到和时间流动的表征相同的方向。

3.以下四个因素：1）任务的时间复杂性，2）空间信息的重叠，3）多任务的适应性，4）任务的时间可预期性，可能就是在本文模型中未能考虑进去，但却影响了实际大脑，从而使得实际大脑中时间信息更高的原因。

由这三个结论，可以推导出一些实验上的预测。例如，在对神经元信号的记录中，若看到了类似于固定轨迹或时间缩放的现象，或许就意味着此时被试正在进行着时间信号的接收或复现。而如果看到了神经元活动中有较大的成分在表征时间信息，其可能正意味着某些大感受野的神经元正在任务中起着作用。

最后，作者还提到，这篇文章中讨论的时间信息仅限于较短的，单次的时间间隔。当时间间隔比较长（>1200ms），或者时间间隔以重复的节奏形式出现时，大脑采取的策略将有所不同，因此不在此文章中讨论。

原文

Bi, Z., & Zhou, C. (2020). Understanding the computation of time using neural network models. Proceedings of the National Academy of Sciences, 117(19), 10530-10540.

推送编辑：罗明浩