详解贝叶斯张量网络：概率性图像识别

Posted 2021-04-07 量子智能俱乐部

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了详解贝叶斯张量网络：概率性图像识别相关的知识，希望对你有一定的参考价值。

导语

论文题目：

Bayesian Tensor Network with Polynomial Complexity for Probabilistic Machine Learning

（注：最近arXiv好像不稳定，可进scirate阅读arXiv论文或相关引文）:

https://arxiv.org/abs/1912.12923,

https://scirate.com/arxiv/1912.12923

GitHub:

https://github.com/ranshiju/BayesianTN

论文作者ResearchGate：

https://www.researchgate.net/profile/Shi_Ju_Ran

概率性图像识别

1. 贝叶斯公式与贝叶斯信念网络

概率性图像识别的核心思想是将特征（或像素）映射成互不相容事件集的概率分布，最终建立这些事件集与分类之间的条件概率，从而实现图形识别。经过映射之后的样本空间是指数大的，类比于张量网络的高效量子态表示，BTN利用多项式的复杂度高效地表示出了该空间中的条件概率。

概率性图像识别的第一步是将特征映射成事件集的概率分布。考虑一张由（M*N）个像素构成的图片，其中每一个像素（记为x[m,n]）取值为0到1之间。那么我们假设有一组互不相容事件，其概率分布由对应的像素值确定。例如，其我们设其概率满足如下关系：

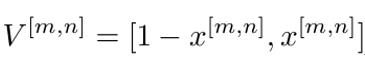
V[m,n]是一个二维向量，和上文一样，每个元素值给出对应事件发生的概率。显然，V[m,n]的norm-1模为1。上式将特征值映射为概率分布，称之为概率映射。下面，我们借鉴张量网络机器学习中的特征映射[8-10]，给出一个从特征值映射到d维概率向量的概率映射（d维人为给定的大于1的整数）

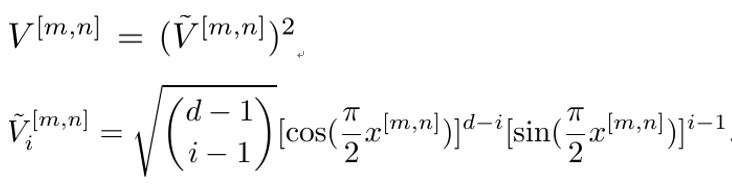
为了理解概率映射的意义，我们先举一个简单的例子，即考虑黑白二值图，图片的像素只能取0（黑）或1（白）。显然，在给定的一张图片里，一个像素不能同时既是黑色又是白色，即两个事件互不相容，所以当像素为黑时，概率分布取[1, 0]，即100%为发生第一个事件；当像素为白时，概率分布取[0, 1]，即100%发生第二个事件。可以看出，第一个事件可认为是“像素为黑色”，第二个事件为“像素为白色”。上文的两个概率映射（第二个取d=2），均给出了这样的概率分布。

在这里，互不相容是理所当然的，其在数学上的表示是：两个互不相容事件对应的概率向量V正交，例如，黑色[1, 0]与白色[0, 1]正交。这种情况下，对于任意一个单位向量有明确的概率意义，例如[0.2, 0.8]代表第一个事件（黑色）发生的概率为0.2，第二个事件（白色）发生的概率为0.8。可以看出，两个事件对应的正交向量[1, 0]和[0, 1]构成展开任意向量的正交完备基，此时，样本空间被等效成为了向量空间。

当事件集的维数（即向量V的维数）小于特征可取的值的个数时，事件就变得有意思了。考虑一个灰度图，每一个像素有256个可能得取值（设取值范围为0到1之间）。如果我们采用第二种概率映射，并取d=256，则不会存在任何问题，但是会由于d太大而导致运算成本极高而难以计算。

维数d小于特征可取的值个数的直接后果，就是本来应该互不相容的事件失去了不相容性，对概率向量的解释也失去了唯一性。例如，我们将灰度值0.1放入第一个概率映射，得到的结果是[0.9, 0.1]，如果仅从这个概率向量出发，其可以被解释为当前像素有100%的概率为0.1灰，也可被解释为像素有90%的可能性为黑色，10%的可能性为白色。换句话说，这256个不相容事件对应的概率向量不相互正交了，那么使用这些向量对任意归一向量的展开也就不唯一了。

在经典概率的范畴下，上述的非正交性或非唯一性可看作是一种近似，笔者认为，这不但不会引起问题，反而会带来新的惊喜。首先，这么做是合理的。对于灰度图的情况，我们仍然可以将黑值和白值对应的概率向量看作向量空间的正交归一基底，那么，灰值对应的概率向量在这组基底下的展开是唯一的。明显，灰值变成了黑与白的“概率叠加”。实际上，从光学的角度，灰确实是可以看成是黑与白的叠加。

既然用到了“概率叠加”这个词，就不得不说起量子态的概率叠加（super-position）。前面我们提到，概率映射是受张量网络机器学习中的特征映射启发而来的，而特征映射就是将一个像素映射成一个量子比特的量子态，其用一个norm-2归一的向量表示概率振幅（amplitude）。如果这个向量的维数小于特征可取值的个数的话，也会存在解释的不唯一性。但这个不唯一性在量子语言里是极为自然的！例如，对于第二种映射，向量[0.6, 0.8]可解释为该像素灰度值100%的概率为x=arccos(0.6*2/pi)，也可理解为该像素灰度值36%的概率为黑，64%的概率为白。对于量子态，这两种解释自然地对应于两种不同基底下的量子测量（quantum measurement）而已。

需要注意的是，BTN描述的是经典概率，满足的是norm-1归一而非norm-2。但神奇的是，经典概率的概率叠加仍然是可行的，且取得了不错的效果（见文中计算结果）。这促使我们思考，同样是基于张量网络的机器学习概率模型，经典概率模型和量子概率模型之间的关系又是什么？本质差别又是什么？现阶段，研究量子机器学习是人工智能领域中的一股热潮，那么“量子”的优势到底是什么？这些问题都亟待进一步的探索与回答。

有了概率映射后，一个像素被映射成了一个事件集的概率分布，那么，一张图片被映射成了多个事件集的联合概率，且不同事件集之间是相互独立的。将这些事件集作为BTN根指标对应的事件集，那么根据BTN的性质（上文第3条，arXiv论文中第f条性质），在给定根指标事件集概率分布的情况下，叶指标事件集的概率分布，也就是我们想要计算的用于分类的条件概率，可由概率向量与BTN的收缩计算求得。

旋转优化算法

上文我们说明了，在任意给定样本（如图片）的情况下如何计算对应的其分类的条件概率。那么，对于给定数据集，我们可以通过最小化损失函数，来对BTN中的贝叶斯张量进行优化，极小化分类误差，实现监督性机器学习。优化的总体思路与神经网络一致，从图片到根事件集概率到分类的条件概率，可视为正向行走（forward）过程，根据正向行走的结果，计算损失函数关于各级贝叶斯张量的梯度，并通过梯度优化张量，即为反向传播（back propagation）过程。

与神经网络不同的是，BTN的优化是带约束的，约束条件就是贝叶斯张量需要满足的归一化条件（见贝叶斯张量性质（b））。论文指出，如果直接使用神经网络常用的优化器（例如SGD，Adam等）进行无约束优化后，再手动对张量进行归一化，这样做会使得更新进入一个非常糟糕的局域不动点（见下图或文中图5）。针对这个问题，文章利用归一化条件，提出了旋转优化（rotation optimization）算法。

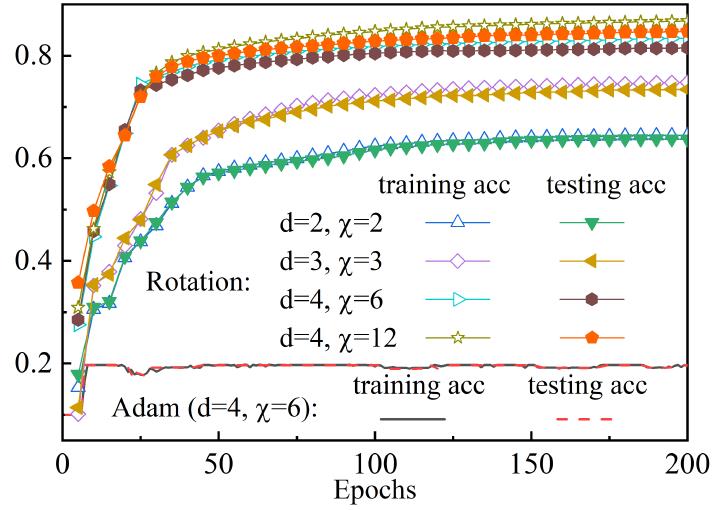
旋转更新与直接使用Adam优化器的收敛结果对比

旋转优化算法来源于一种针对概率模型的切空间优化方法（tangent-space gradient optimization, TSGO [11]），核心思想是将梯度更新视为参数向量的旋转，好处是既能通过旋转角度控制更新强度，从而避免梯度消失和爆炸问题，又能保持概率模型要求的归一化条件。论文详细给出了旋转更新的相关计算公式，这里由于输入不便，就不赘述了。在fashion-MNIST的计算结果如上图（论文图5）。需要说明的是，无论是旋转优化还是TSGO，其应用范围都不限于张量网络模型，有些“神似”于Hinton等提出的神经网络层归一化（layer normalization）[12]，笔者认为，其中区别在于，神经网络的层归一化很难用数学去解释其可行性或效果，这可能是由于神经网络本身的可解释性较弱。而TSGO或旋转更新中涉及的归一化，是基于概率模型的归一化要求，且更新过程也具备更清晰的图景与更高的可解释性。当然，这也得益于概率模型较高的可解释性。

作者在论文中强调，所得结果并不是为了说明Adam优化器在BTN上失效。如何将Adam有效地用于BTN及其相关的带约束优化问题，例如加入惩罚项（拉格朗日乘子）等，是一个开放性问题。对于BTN，应该是需要严格保持归一性的，否则其概率基础会出现问题。加入惩罚项并不能保证归一化约束的严格成立。但是从数值算法的角度考虑，也有可能在约束近似成立的情况下，模型仍可以获得好的结果。这些问题都需要进一步的研究。

【未完待续】

参考文献

[8] E. Stoudenmire and D. J. Schwab. Supervised learning with tensor networks, in Advances in Neural Information Processing Systems. 2016: 4799-4807.

[9] D. Liu, et al. Machine learning by unitary tensor network of hierarchical tree structure. New J. Phys. 21, 073059 (2019).

[10] Z.-Y. Han, J. Wang, H. Fan, L. Wang, and P. Zhang. Unsupervised Generative Modeling Using Matrix Product States. Phys. Rev. X 8, 031012 (2018).

[11] Z.-Z. Sun, S.-J. Ran, and G. Su, Tangent-Space Gradient Optimization of Tensor Network for Machine Learning. In preparation.

[12] J. L. Ba, J. R. Kiros, and G. E. Hinton. Layer Normalization. arXiv:1607.06450 (2016).

未

完

待

续