如果记小于n且与n互质的数的个数为Φ(n),则在数论上叫函数Φ(n)为欧拉函数,求Φ(60)
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如果记小于n且与n互质的数的个数为Φ(n),则在数论上叫函数Φ(n)为欧拉函数,求Φ(60)相关的知识,希望对你有一定的参考价值。
如果记小于n且与n互质的数的个数为Φ(n),则在数论上叫函数Φ(n)为欧拉函数,求Φ(60)
要过程
不要枚举,欧拉函数是不是有公式
是什么,怎么证明
第二个回答里的地址正解,有一个定理如下图:这里μ(n)是莫比乌斯函数
为计算方便还有以下性质
φ(p^a)=p^a-p^(a-1),p是素数
φ(mn)=φ(m)φ(n)(d/φ(d)),d=(m,n)
计算φ(60)就不困难了
可以参考T. Apostol 的Introduction to Analytical Number Theory;第二章里有关于基本的算数的函数的性质的讨论
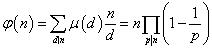
高斯曾经研究过这个问题,似乎没有得出答案。
或者这个公式是个超越函数,仍然需要枚举……
上面的链接中并没有写出我们想要的公式,同余(mud)也是需要枚举的。 参考技术B 你要的在下面,请看
参考资料:http://baike.baidu.com/view/107769.htm?fr=ala0_1
参考技术C 1数论--欧拉函数
欧拉函数,用φ(n)表示
欧拉函数是求小于等于n的数中与n互质的数的数目
比如φ(10),小于等于10的数中与10互质的数有1,3,7,9,所以φ(10)=4
那么,问题来了,如何求求小于等于n的数中与n互质的数的数目???
比如求φ(10)
先质因子分解,10=2*5,再去掉所有2和5的倍数:2的倍数2,4,6,8,10;5的倍数:5,10;
10-10/2-10/5,但是这样算10去掉了两次,那就加回来,10-10/2-10/5+10/2/5=4(容斥原理)
φ(10)=4;
再比如φ(30)
30=2*3*5;
30-30/2-30/3-30/5+ 30/(2*3) + 30/(2*5) + 30/(3*5) - 30/(2*3*5)=8
φ(30)=8
但是这样算太麻烦了!
看简单方法:
φ(30) = 30*(1 - 1/2)*(1 - 1/3)*(1 - 1/5) = 30*(1 - 1/2 - 1/3 - 1/5 + 1/6 + 1/10 + 1/15 - 1/30)
可以发现吧,展开后(划线的)跟上面那个式子(斜体的)其实是一样的
于是,可以写代码:
1 #include<cstdio> 2 3 int phi(int x){//欧拉函数 4 int ans = x; 5 for(int i = 2; i*i <= x; i++){ 6 if(x % i == 0){ 7 ans = ans / i * (i-1); 8 while(x % i == 0) x /= i; 9 } 10 } 11 if(x > 1) ans = ans / x * (x-1); 12 return ans; 13 } 14 15 int main() 16 { 17 printf("%d\\n",phi(30)); 18 }
时间复杂度为O(√n)
如果要预处理n个数的欧拉函数值,可以用筛子的思想(还记得前面提到的素数筛吗??)
#include<cstdio> const int N = 100000 + 5; int phi[N]; void Euler(){ phi[1] = 1; for(int i = 2; i < N; i ++){ if(!phi[i]){//类似素数筛,phi[i]==0代表i是素数 for(int j = i; j < N; j += i){ if(!phi[j]) phi[j] = j; phi[j] = phi[j] / i * (i-1);//i一定是j的素因子 (看for循环环里面的j的变化) } } } } int main(){ Euler(); printf("%d\\n",phi[30]); }
性质:
p为质数
1. phi(p)=p-1 因为质数p除了1以外的因数只有p,故1至p的整数只有p与p不互质
2. 如果i mod p = 0, 那么 phi(i * p)=phi(i) * p //例:10%2==0,phi(2*10)=phi(10)*2=4*2=8 正解
3.若i mod p ≠0, 那么 phi( i * p )=phi(i) * ( p-1 ) //例:10%3!=0,phi(3*10)=phi(10)*(3-1)=4*2=8 正解
公式:
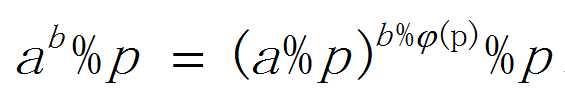
超欧拉取模进化公式
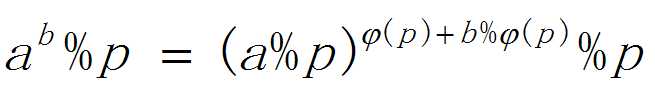
以上是关于如果记小于n且与n互质的数的个数为Φ(n),则在数论上叫函数Φ(n)为欧拉函数,求Φ(60)的主要内容,如果未能解决你的问题,请参考以下文章